Titration of a Weak Acid with a Strong Base

A titration is a controlled chemical reaction between two different solutions.

Introduction

The titration of a weak acid with a strong base involves the direct transfer of protons from the weak acid to the hydoxide ion. The reaction of the weak acid, acetic acid, with a strong base, NaOH, can be seen below. In the reaction the acid and base react in a one to one ratio.

\[C_2H_4O_{2(aq)} + OH^-_{(aq)} \rightarrow C_2H_3O^-_{2(aq)} + H_2O_{(l)} \label{1}\]

In this reaction a buret is used to administer one solution to another. The solution administered from the buret is called the titrant. The solution that the titrant is added to is called the analyte. In a titration of a Weak Acid with a Strong Base the titrant is a strong base and the analyte is a weak acid. In order to fully understand this type of titration the reaction, titration curve, and type of titration problems will be introduced.

Figure \(\PageIndex{1}\): Titrations involve the addition of the titrant from the burret to the analyte. Figure is used with the permission of J.A. Freyre.

The Titration Curve

The titration curve is a graph of the volume of titrant, or in our case the volume of strong base, plotted against the pH. There are several characteristics that are seen in all titration curves of a weak acid with a strong base. These characteristics are stated below.

1. The initial pH (before the addition of any strong base) is higher or less acidic than the titration of a strong acid
2. There is a sharp increase in pH at the beginning of the titration. This is because the anion of the weak acid becomes a common ion that reduces the ionization of the acid.
3. After the sharp increase at the beginning of the titration the curve only changes gradually. This is because the solution is acting as a buffer. This will continue until the base overcomes the buffers capacity.
4. In the middle of this gradually curve the half-neutralization occurs. At this point the concentration of weak acid is equal to the concentration of its conjugate base. Therefore the pH=pK_a. This point is called the half-neutralization because half of the acid has been neutralized.
5. At the equivalence point the pH is greater then 7 because all of the acid (HA) has been converted to its conjugate base (A-) by the addition of NaOH and now the equilibrium moves backwards towards HA and produces hydroxide, that is: \[A^- + H_2O \rightleftharpoons AH + OH^-\]
6. The steep portion of the curve prior to the equivalence point is short. It usually only occurs until a pH of around 10.

The image of a titration curve of a weak acid with a strong base is seen below. All of the characteristics described above can be seen within it.

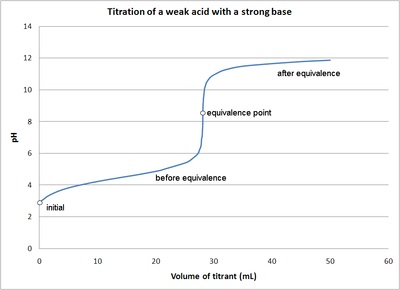
Figure \(\PageIndex{2}\): The titration of a weak acid with strong base. Figure is used with the permission of J.A. Freyre under the Creative Commons Attributions-Share Alike 2.5 Generic

Weak Acid and Strong Base Titration Problems

When solving a titration problem with a weak acid and a strong base there are certain values that you want to attain. These include the initial pH, the pH after adding a small amount of base, the pH at the half-neutralization, the pH at the equivalence point, and finally the pH after adding excess base. This data will give sufficient information about the titration. Below is an example of this process.

Find the pH at each of the following points in the titration of 25 mL of 0.3 M HF with 0.3 M NaOH. The \(k_a\) value is \(6.6\times 10^{-4}\)

1. The initial pH
2. After adding 10 mL of 0.3 M NaOH
3. After adding 12.50 mL of 0.3 M NaOH
4. After adding 25 mL of 0.3 M NaOH
5. After adding 26 mL of 0.3 M NaOH

Example \(\PageIndex{1}\): Calculating the Initial pH

Finding the initial pH.

SOLUTION

Since HF is a weak acid, the use of an ICE table is required to find the pH. The question gives us the concentration of the HF.

\[ HF + H_2O \rightleftharpoons H_3O^+ + F- \nonumber \]

	HF	H2O	H3O^+	F^-
Initial	0.3 M	-	0 M	0 M
Change	- X	-	+ X	+X
Equilibrium	0.3 - X	-	X M	X M

Writing the information from the ICE Table in Equation form yields

\[6.6\times 10^{-4} = \dfrac{x^{2}}{0.3-x} \nonumber\]

Manipulating the equation to get everything on one side yields

\[0 = x^{2} + 6.6\times 10^{-4}x - 1.98\times 10^{-4} \nonumber \]

Now this information is plugged into the quadratic formula to give

\[x = \dfrac{-6.6\times 10^{-4} \pm \sqrt{(6.6\times 10^{-4})^2 - 4(1)(-1.98\times 10^{-4})}}{2} \nonumber \]

The quadratic formula yields that x=0.013745 and x=-0.014405

However we can rule out x=-0.014405 because there cannot be negative concentrations. Therefore to get the pH we plug the concentration of H₃O⁺ into the equation pH=-log(0.013745) and get pH=1.86

Example \(\PageIndex{2}\): After adding 10 mL of 0.3 M NaOH

Find the pH after the addition of 10 mL of 0.3 M NaOH.

SOLUTION

• The number of millimoles of HF to be neutralized is \[(25 \,mL)\left(\dfrac{0.3\, mmol \,HF}{1\, mL}\right) = 7.50 mmol HF \nonumber \]
• The number of millimoles of OH^_ that will be added within 10 mL is \[(10 \,mL)\left(\dfrac{0.3 \,mmol\, OH^-}{1\, mL}\right) = 3\, mmol OH^- \nonumber \]

To calculate the pH with this addition of base we must use an ICE Table

\[ HF + H_2O \rightleftharpoons H_3O^+ + F- \nonumber \]

	HF	H2O	H3O^+	F^-
Initial	7.5 mmol	0 mmol	-	0 mmol
Add	0 mmol	3 mmol	-
Change	-3 mmol	-3 mmol	-	3 mmol
Equilibrium	4.5 mmol	0 mmol	-	3 mmol

However, this only gives us the millimoles. To get the concentration we must divide by the total volume. The total volume is the 25 mL original solution of HF plus the 10 mL of NaOH that was added. Therefore, the total volume is \(25 mL + 10 mL = 35 mL\)

• Concentration of HF: \[\dfrac{4.5\,mmol\, HF}{35\,mL} = 0.1287\;M\]
• Concentration of F^-: \[\dfrac{3m\,mol F^-}{35\, mL} = 0.0857\;M\]

Since an acid and its conjugate base are in equilibrium we can attempt to use the Henderson-hasselbalch equation. However, for this to work the reaction must follow certain rules. The ratio of the conjugate base and weak acid must be between 0.10 and 10. Also, both the ratio of the conjugate base and k_a value and the ratio of the acid and k_a value must exceed 100.

In this problem the Henderson-hasselbalch equation can be applied because the ratio of F- to HF is \(\frac{0.0857}{0.1287} = 0.666\) . This is between 0.10 and 10. The ratio of HF to k_a is \(\frac{0.1287M}{6.6 \times 10^{-4}} = 195\) and the ratio of F^- to k_a is \(\frac{0.0857M}{6.6 \times 10^{-4}} =130\). These both exceed one hundred. Therefore, we continue by using the Henderson-hasselbalch equation.

\(pH=pk_{a} + \log\dfrac{[A^{-}]}{[HA]}\)

\(pH=-\log(6.6\times 10^{-4}) + \log\dfrac{.0857}{.1287}\)

pH=3.00

Example \(\PageIndex{3}\): After adding 12.50 mL of 0.3 M NaOH

Find the pH after adding 12.50 mL of 0.3 M NaOH.

SOLUTION

The millimoles of OH^- added in 12.50 mL: \(12.50 mL * \dfrac{.3 mmol OH^{-}}{mL} =3.75 mmol OH^{-}\)

Once again we must use an ICE Table

	HF	H2O	H3O^+	F^-
Initial	7.5 mmol	0 mmol	-	0 mmol
Add	0 mmol	3.75 mmol	-
Change	-3.75 mmol	-3.75 mmol	-	3.75 mmol
Equilibrium	3.75 mmol	0 mmol	-	3.75 mmol

To find the concentrations we must divide by the total volume. This is the initial volume of HF, 25 mL, and the addition of NaOH, 12.50 mL. Therefore the total volume is 25 mL + 12.50 mL = 37.50 mL

• Concentration of HF: \(\dfrac{3.75mmol HF}{37.50mL} = 0.1M\)
• Concentration of F^-: \(\dfrac{3.75mmol F^{-}}{37.50mL} = 0.1M\)

We have found the Half-neutralization point. We know this because the total amount of acid to be neutralized, 7.50mmol, has been reduced to half of its value, 3.75 mmol. At the half-neutralization point we can simplify the Henderson-Hasselbalch equation and use it. Since the amount of conjugate base and acid are equal, their ratio is one. We know that \(log(1) =0\) and therefore the ratio of conjugant base to acid will be zero as well. The equation at the half-neutralization point will be \(pH=pk_{a} +log(1)\) which equals \(pH=pk_{a}\)

\(pH=-log(6.6\times 10^{-4})\)

pH=3.18

Example \(\PageIndex{4}\): After adding 25 mL of 0.3 M NaOH

Find the pH after the addition of 25 mL of NaOH.

SOLUTION

• The millimoles of OH^- added in 25 mL:\(25mL* \dfrac{.3mmol OH^{-}}{1mL} =7.5 mmol OH^{-}\)

	HF	H2O	H3O^+	F^-
Initial	7.5 mmol	0 mmol	-	0 mmol
Add	0 mmol	+7.5 mmol	-	0 mmol
Change	-7.5 mmol	-7.5 mmol	-	7.5 mmol
Equilibrium	0 mmol	0 mmol	-	7.5 mmol

This is the equivalence point of the titration. We know this because the acid and base are both neutralized and neither is in excess. To find the concentrations we must divide by the total volume. This is the initial volume of HF, 25 mL, and the addition of NaOH, 25 mL. Therefore the total volume is 25 mL + 25 mL = 50 mL

Concentration of F^-:\(\dfrac{7.5 mmol F^{-}}{50 mL}=0.15M\)

However, to get the pH at this point we must realize that F^- will hydrolyze. An ICE table for this reaction must be constructed

	HF	H2O	H3O^+	F^-
Initial	0.15 M	-	0 M	0 M
Change	- X	-	+ X	+X
Equilibrium	0.15 - X	-	X M	X M

In this reaction the F^- acts as a base. Therefore we must obtain the k_b value instead of the k_a value.

\(k_{b}= \dfrac{k_{w}}{k_{a}}\)

\(k_{b} = \dfrac{1.0\times 10^{-14}}{6.6\times 10^{-4}}\)

\(k_{b}=1.515\times 10^{-11}\)

Now that we have the k_b value, we can write the ICE table in equation the equation form

\(1.515\times 10^{-11} \dfrac{x^{2}}{.15-x}\)

Manipulating the equation to get everything on one side yields

\(0= x^{2} + 1.515 \times 10^{-11}x -2.2727\times 10^{-12}\)

Now this information is plugged into the quadratic formula to give

\(x = \dfrac{-1.515\times 10^{-11} \pm \sqrt{(-1.515\times 10^{-11})^2 - 4(1)(-2.2727\times 10^{-12})}}{2}\)

The quadratic formula yields x=1.5075\times 10^-6 and -1.5075\times 10^-6 . However the negative value can be ruled out because concentrations cannot be zero.

Therefore to get the pOH we plug the concentration of OH^- into the equation pH=-log(1.5075\times 10^-6) and get pOH=5.82. To get the pH we minus the pOH from 14.

pH=14 - 5.82

pH= 8.18

Example \(\PageIndex{5}\): After adding 26 mL of 0.3 M NaOH

Find the pH after the addition of 26 mL of NaOH.

SOLUTION

The millimoles of OH^- added in the 26 mL: \(26 mL * \dfrac{.3 mmol OH^{-1}}{1 mL} = 7.8 mmol OH^{-}\)

This amount is greater then the moles of acid that is present. The 7.8 mmol OH^- neutralizes the 7.50 mmol HCl. To find how much OH^- will be in excess we subtract the amount of acid and hydroxide.

mmoles of hydroxide in excess: 7.8 mmol - 7.50 mmol= 0.3 mmol OH^-

To find the concentration of the OH^- we must divide by the total volume. This is the initial volume of HF, 25 mL, and the addition of NaOH, 26 mL. Therefore the total volume is 25 mL + 26 mL = 51 mL

The concentration of OH^- is \(\dfrac{0.3 mmol OH^{-}}{51 mL}=0.00588M\)

pOH=-log(0.00588)=2.23

pH=14-2.23

pH=11.77

Example \(\PageIndex{6}\): Equivalence Point

When does the equivalence point of 15 mL of 0.15 M CH₃COOH titrated with 0.1 M NaOH occur?

SOLUTION

The equivalence point occurs when equal moles of acid react with equal moles of base.

The mmol CH₃COOH:

\(15 mL CH_{3}COOH * \dfrac{.15 mmol CH_{3}COOH}{1 mL} =2.25 mmol CH_{3}COOH\)

We must find the amount of of mL of NaOH to give us the same mmols as CH₃COOH

\(2.25 mmol CH_{3}COOH = 0.1M NaOH* XmL NaOH\)

X=22.5 mL

Therefore the equivalence point is after the addition of 22.5 mL of NaOH

References

1. Levie, Robert De. Aqueous Acid-Base Equilibrium and Titrations. New York: Oxford University Press Inc. 1991
2. Petrucci, Ralph H. General Chemistry: Principles & Modern Application, 9th Edition. New Jersey: Pearson Prentice Hall. 2007.

Outside Links

1. http://www.youtube.com/watch?v=wgIXYvehTC4
2. http://www.youtube.com/watch?v=266wzpPXeXo

Contributors

• Hyejung Sohn (UCD), Jessica Thornton (UCD)