Electrolytic Cells

Voltaic cells are driven by a spontaneous chemical reaction that produces an electric current through an outside circuit. These cells are important because they are the basis for the batteries that fuel modern society. But they are not the only kind of electrochemical cell. The reverse reaction in each case is non-spontaneous and requires electrical energy to occur.

Introduction

The general form of the reaction can be written as:

\[ \underset{\longleftarrow \text{Non spontaneous}}{\overset{\text{Spontaneous} \longrightarrow}{\text{Reactants} \rightleftharpoons \text{Products} + \text{Electrical Energy}}} \nonumber \]

It is possible to construct a cell that does work on a chemical system by driving an electric current through the system. These cells are called electrolytic cells. Electrolytic cells, like galvanic cells, are composed of two half-cells--one is a reduction half-cell, the other is an oxidation half-cell. The direction of electron flow in electrolytic cells, however, may be reversed from the direction of spontaneous electron flow in galvanic cells, but the definition of both cathode and anode remain the same, where reduction takes place at the cathode and oxidation occurs at the anode. Because the directions of both half-reactions have been reversed, the sign, but not the magnitude, of the cell potential has been reversed.

Electrolytic cells are very similar to voltaic (galvanic) cells in the sense that both require a salt bridge, both have a cathode and anode side, and both have a consistent flow of electrons from the anode to the cathode. However, there are also striking differences between the two cells. The main differences are outlined below:

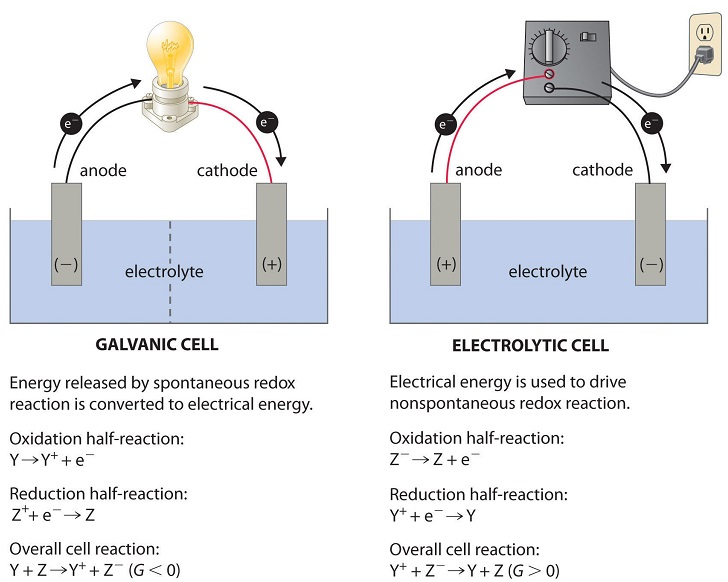
Figure \(\PageIndex{1}\): Electrochemical Cells. A galvanic cell (left) transforms the energy released by a spontaneous redox reaction into electrical energy that can be used to perform work. The oxidative and reductive half-reactions usually occur in separate compartments that are connected by an external electrical circuit; in addition, a second connection that allows ions to flow between the compartments (shown here as a vertical dashed line to represent a porous barrier) is necessary to maintain electrical neutrality. The potential difference between the electrodes (voltage) causes electrons to flow from the reductant to the oxidant through the external circuit, generating an electric current. In an electrolytic cell (right), an external source of electrical energy is used to generate a potential difference between the electrodes that forces electrons to flow, driving a nonspontaneous redox reaction; only a single compartment is employed in most applications. In both kinds of electrochemical cells, the anode is the electrode at which the oxidation half-reaction occurs, and the cathode is the electrode at which the reduction half-reaction occurs.

Table \(\PageIndex{1}\): Properties of Galvanic and Electrochemical Cells

Electrochemical cell (Galvanic Cell)	Electrolytic cell
A Galvanic cell converts chemical energy into electrical energy.	An electrolytic cell converts electrical energy into chemical energy.
Here, the redox reaction is spontaneous and is responsible for the production of electrical energy.	The redox reaction is not spontaneous and electrical energy has to be supplied to initiate the reaction.
The two half-cells are set up in different containers, being connected through the salt bridge or porous partition.	Both the electrodes are placed in a same container in the solution of molten electrolyte.
Here the anode is negative and cathode is the positive electrode. The reaction at the anode is oxidation and that at the cathode is reduction.	Here, the anode is positive and cathode is the negative electrode. The reaction at the anode is oxidation and that at the cathode is reduction.
The electrons are supplied by the species getting oxidized. They move from anode to the cathode in the external circuit.	The external battery supplies the electrons. They enter through the cathode and come out through the anode.

Electrolytic Cells

To explain what happens in an electrolytic cell let us examine the decomposition of molten sodium chloride into sodium metal and chlorine gas. The reaction is written below.

---------> Non spontaneous ( electrolytic cell )
2 Na Cl (l)	\(\rightleftharpoons\)	2 Na (s)	+	Cl2 (g)
<--------- Spontaneous ( electrochemical cell )

If molten \(NaCl_{(l)}\) is placed into the container and inert electrodes of \(C_{(s)}\) are inserted, attached to the positive and negative terminals of a battery, an electrolytic reaction will occur.

1. Electrons from the negative terminal travel to the cathode and are used to reduce sodium ions into sodium atoms. The sodium will plate onto the cathode as it forms. The sodium ion are migrating towards the cathode. \[ Na^+ + e^- \rightleftharpoons Na_{(s)} \nonumber \]
2. The negative Chlorine ions migrate towards the anode and release electrons as they oxidize to form chlorine atoms. The chlorine atoms will combine together to form chlorine gas which will bubble away. \[ 2Cl^- \rightleftharpoons Cl_{2 (g)} + 2e^- \nonumber \]
3. Note that the site of oxidation is still the anode and the site of reduction is still the cathode, but the charge on these two electrodes are reversed. Anode is now positive charged and the cathode has a negative charged.
4. The conditions under which the electrolyte cell operates are very important. The substance that is the strongest reducing agent (the substance with the highest standard cell potential value in the table) will undergo oxidation. The substance that is the strongest oxidizing agent will be reduced. If an aqueous solution of sodium chloride were used in the above system, hydrogen would undergo reduction instead of sodium, because it is a stronger oxidizing agent that sodium.

Predicting Electrolysis Reaction

There are four primary factors that determine whether or not electrolysis will take place even if the external voltage exceeds the calculated amount:

1. An overpotential or voltage excess is sometimes needed to overcome interactions at the electrode surface. This case happens more frequently with gases. E.g. H₂ (g) requires a 1.5 V overpotential, while Pt (s) requires 0 V overpotential
2. There might be more than one electrode reaction that occurs meaning that there may be more than one half-reaction leaving two or more possibilities for the cell reaction.
3. The reactants may be in nonstandard conditions which means that the voltage for the half cells may be less or more than the standard condition amount. For Example:

• Concentration of chloride ion = 5.5M not the unit activity of 1M. This means that the reduction of chloride = 1.31V not 1.36V
• The standard condition is to have a pH of 4 in the anode half cell but sometimes during nonstandard states, the pH may be higher or lower changing the voltage.

4. An inert electrode’s ability to electrolysis depend on the reactants in the electrolyte solution while an active electrode can run on its own to perform the oxidation or reduction half reaction.

If all four of these factors are accounted for, we can successfully predict electrode half reactions and overall reactions in electrolysis.

Exercise \(\PageIndex{1}\)

Predict the electrode reactions and the overall reaction when the anode is made of (a) copper and (b) platinum.

Quantitative Aspects of Electrolysis

Michael Faraday discovered in 1833 that there is always a simple relationship between the amount of substance produced or consumed at an electrode during electrolysis and the quantity of electrical charge Q which passes through the cell. For example, the half-equation

\[Ag^+ + e^– \rightarrow Ag \nonumber \]

tells us that when 1 mol Ag⁺ is plated out as 1 mol Ag, 1 mol e^– must be supplied from the cathode. Since the negative charge on a single electron is known to be 1.6022 × 10^–19 C, we can multiply by the Avogadro constant to obtain the charge per mole of electrons. This quantity is called the Faraday Constant, symbol F:

F = 1.6022 × 10^–19 C × 6.0221 × 10²³ mol^–1 = 9.649 × 10⁴ C mol^–1

Thus in the case of Eq. (1), 96 490 C would have to pass through the cathode in order to deposit 1 mol Ag. For any electrolysis the electrical charge Q passing through an electrode is related to the amount of electrons n_e– by

\[F=\dfrac{Q}{n_{e^-}} \nonumber \]

Thus F serves as a conversion factor between \(n_{e^-}\) and \(Q\).

Often the electrical current rather than the quantity of electrical charge is measured in an electrolysis experiment. Since a coulomb is defined as the quantity of charge which passes a fixed point in an electrical circuit when a current of one ampere flows for one second, the charge in coulombs can be calculated by multiplying the measured current (in amperes) by the time (in seconds) during which it flows:

\[Q = It \nonumber \]

In this equation I represents current and t represents time. If you remember that

coulomb = 1 ampere × 1 second 1 C = 1 A s

you can adjust the time units to obtain the correct result. Now that we can predict the electrode half-reactions and overall reactions in electrolysis, it is also important to be able to calculate the quantities of reactants consumed and the products produced. For these calculations we will be using the Faraday constant:

1 mol of electron = 96,485 C

charge (C) = current (C/s) x time (s)

(C/s) = 1 coulomb of charge per second = 1 ampere (A)

Simple conversion for any type of problem:

1. Convert any given time to seconds
2. Take the current given (A) over the seconds, [1 c = (A)/(s)]
3. Finally use the stoichiometry conversion of 1 mol of electron = 96,485 C (Faraday's Constant)

Example \(\PageIndex{1}\)

The electrolysis of dissolved Bromine sample can be used to determine the amount of Bromine content in sample. At the cathode, the reduction half reaction is \[Br^{2+}_{(aq)} + 2 e^- \rightarrow 2 Br^- \nonumber \]. What mass of Bromine can be deposited in 3.00 hours by a current of 1.18 A?

Solution:

3.00 hours x 60 min/hour x 60 sec/1 min x 1.18 C(A) / 1 sec x 1 mol e^-/96,485 C

= 0.132 mol e^-

Problems

1) Predict the products of electrolysis by filling in the graph:

Cl^-, Br^-, I^-, H⁺, OH^-, Cu²⁺, Pb²⁺, Ag+, K⁺, Na⁺,

2) Calculate the quantity of electrical charge needed to plate 1.386 mol Cr from an acidic solution of K₂Cr₂O₇according to half-equation

H₂Cr₂O₇(aq) + 12H⁺(aq) + 12e^– → 2Cr(s) + 7 H₂O(l)

3) Hydrogen peroxide, H₂O₂, can be manufactured by electrolysis of cold concentrated sulfuric acid. The reaction at the anode is

2H₂SO₄ → H₂S₂O₈ + 2H⁺ + 2e^–

When the resultant peroxydisulfuric acid, H₂S₂O₈, is boiled at reduced pressure, it decomposes:

2H₂O + H₂S₂O₈ → 2H₂SO₄ + H₂O₂

Calculate the mass of hydrogen peroxide produced if a current of 0.893 flows for 1 hour.

4) The electrolysis of dissolved Cholride sample can be used to determine the amount of Chloride content in sample. At the cathode, the reduction half reaction is Cl²⁺(aq) + 2 e^- -> 2 Cl^-. What mass of Chloride can be deposited in 6.25 hours by a current of 1.11 A?

5) In an electrolytic cell the electrode at which the electrons enter the solution is called the ______ ; the chemical change that occurs at this electrode is called _______.

1. anode, oxidation
2. anode, reduction
3. cathode, oxidation
4. cathode, reduction
5. cannot tell unless we know the species being oxidized and reduced.

6)How long (in hours) must a current of 5.0 amperes be maintained to electroplate 60 g of calcium from molten CaCl₂?

1. 27 hours
2. 8.3 hours
3. 11 hours
4. 16 hours
5. 5.9 hours

7) How long, in hours, would be required for the electroplating of 78 g of platinum from a solution of [PtCl₆]^2-, using an average current of 10 amperes at an 80% electrode efficiency?

1. 8.4
2. 5.4
3. 16.8
4. 11.2
5. 12.4

8) How many faradays are required to reduce 1.00 g of aluminum(III) to the aluminum metal?

1. 1.00
2. 1.50
3. 3.00
4. 0.111
5. 0.250

9) Find the standard cell potential for an electrochemical cell with the following cell reaction.

Zn(s) + Cu²⁺(aq) → Zn²⁺(aq) + Cu(s)

Answers

1). Cl^- chlorine H⁺ hydrogen

Cl^- chlorine Cu²⁺ copper

I^- iodine H⁺ Hhydrogen

2) 12 mol e^– is required to plate 2 mol Cr, giving us a stoichiometric ratio S(e^–/Cr). Then the Faraday constant can be used to find the quantity of charge.

n_Cr n_e– Q

Q = 1.386 mol Cr × × = 8.024 × 10⁵ C

3) The product of current and time gives us the quantity of electricity, Q. Knowing this we easily calculate the amount of electrons, n_e–. From the first half-equation we can then find the amount of peroxydisulfuric acid, and the second leads to n_H2O2 and finally to m_H2O2.

= 05666 × g H₂O₂ = 0.5666 g H₂O₂

4) 0.259 mol e^-

5) d

6) d

7) b

8) d

9) Write the half-reactions for each process.

Zn(s) → Zn²⁺(aq) + 2 e^-

Cu²⁺(aq) + 2 e^- → Cu(s)

Look up the standard potentials for the reduction half-reaction.

E^o_{reduction of Cu2+} = + 0.339 V

E^o_{reduction of Zn2+} = - 0.762 V

Determine the overall standard cell potential.

E^o_cell = + 1.101 V

References

1. Petrucci, et al. General Chemistry: Principles & Modern Applications. 9th ed. Upper Saddle River, New Jersey: Pearson/Prentice Hall, 2007.
2. Kolbe, Hermann. The Electrolysis of Organic Compounds. Edinburgh : E. & S. Livingstone, 1947.
3. Stuart, A.T. "Electrolysis of water." Hydrogen Production 2001 May 13
4. All of the afformentioned "Outside Links" as well.

Contributors and Attributions

• Jasmine Briones, UC Davis 2012