Solutions to Chapter 3 exercises
- Page ID
- 80379
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)E3.1:

E3.1:
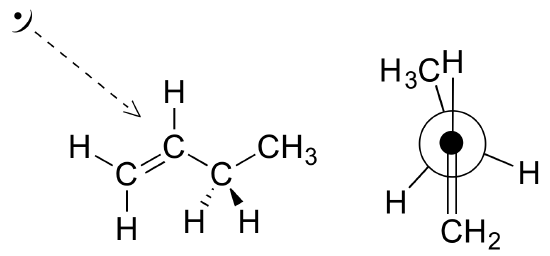
E3.3: Recall from your General Chemistry course that DG0, the standard Gibbs Free Energy change of a reaction (or in this case, a conformational change) is related to the equilibrium constant Keq by:
DG0 = RTlnKeq or Keq = e^(-DG0/RT)
. . . where R is the gas constant 8.314 J mol-1 K-1
Using T = 298K (25oC) and DG0 = -7.0 kJ/mol, we calculate Keq = 17.
Note that DG0 has a negative value because the methyl-axial to methyl-equatorial ring flip is an energetically downhill process. Because the equatorial conformation is more stable, it makes sense that the equilibrium constant for the ring flip is greater than 1.
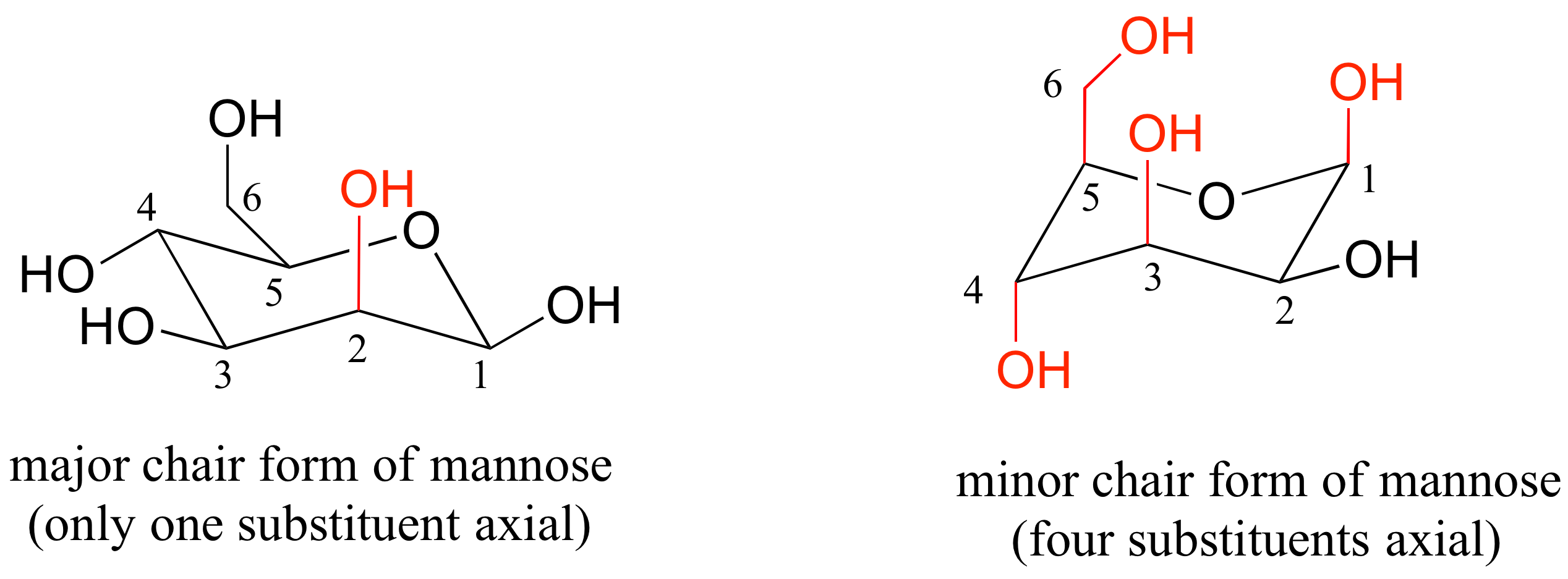
E3.4: Note in (b) that one of the substituents must be in the axial position. In the lower energy chair conformation, it is the smaller methyl group that assumes the axial position.

E3.5: To answer these questions, you will want to draw out the chair conformations of the compounds specified.
a) cis-1,3-dimethylcyclohexane: the two methyl groups are either both equatorial or both axial. In cis-1,4-dimethylcyclohexane, one methyl group is always axial and one equatorial, so the two conformations have the same energy.
b) trans-1,2-dimethylcyclohexane: the two methyl groups are either both equatorial or both axial. In cis-1,2-dimethylcyclohexane, one methyl group is always axial and one equatorial, so the two conformations have the same energy.
c) trans-1-isopropyl-2-methylcyclohexane: both compounds are either diaxial or diequatorial, but the larger isopropyl substituent means that the difference between the diaxial and diequatorial conformations is larger.
E3.6: No. In order to change the relationship of two substituents on a ring from cis to trans, you would need to break and reform two covalent bonds. Ring flips involve only rotation of single bonds
E3.7:
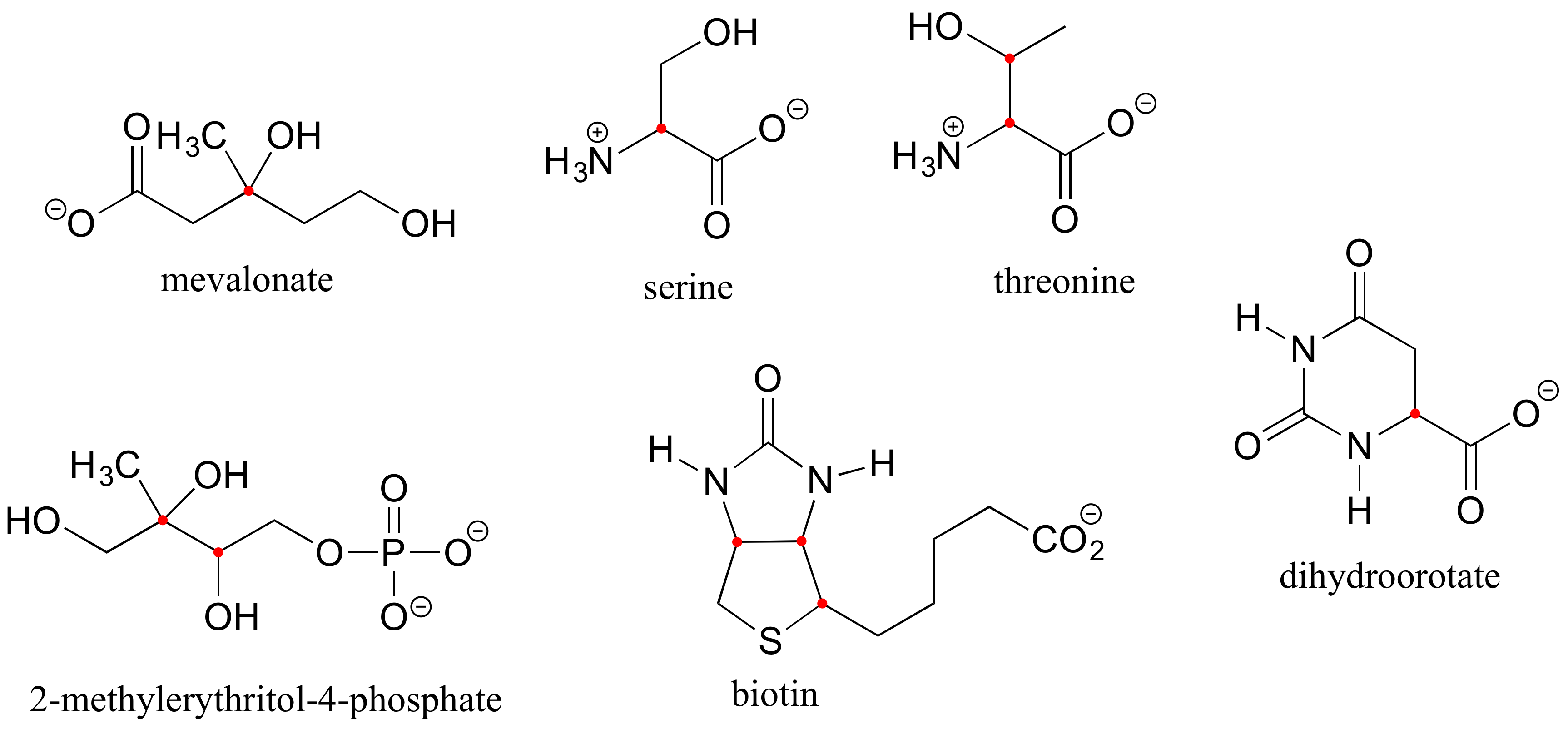
E3.8: Chiral centers are designated with a dot.
E3.9: (there are other ways that the two enantiomers can be drawn correctly - check your drawing with your instructor or tutor)
a)
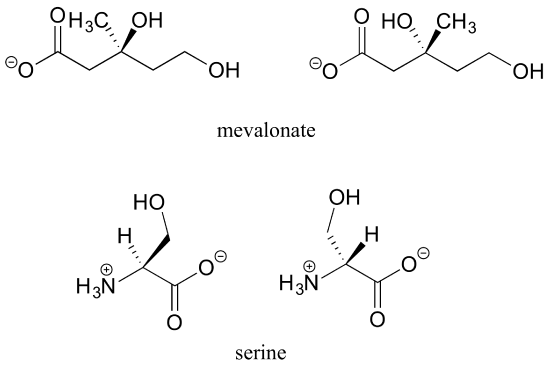
b) No, the two structures are identical. In both drawings, the bond to the OH is pointing out of the plane of the page - it doesn't matter whether the solid wedge is pointing to the left or the right. Make models of the two drawings and you will see they are exactly the same.
E3.10:

E3.11:

E3.12: The C-O bond should be drawn as a dash to get the R configuration.
E3.13:
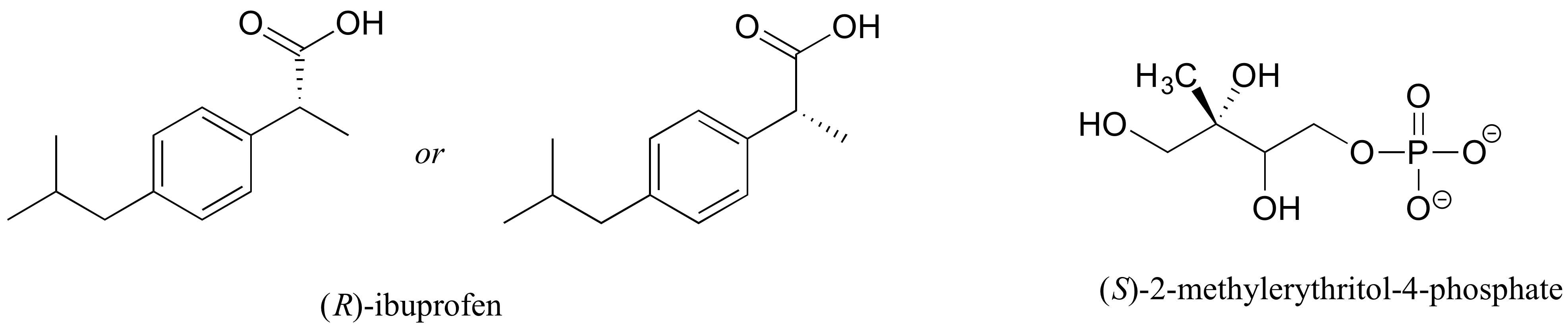
E3.14: The value of c is 7.50 g/100 mL, so using the definition of specific rotation, the observed rotation is expected to be (11.5)(7.5) = 86.3o.
E3.15: The observed rotation of the mixture is levorotary (negative, counter-clockwise), and the specific rotation of the pure R enantiomer is given as dextrorotary (positive, clockwise), meaning that the pure S enantiomer must be levorotary, and the mixture must contain more of the S enantiomer than of the R enantiomer.
E3.16: Cysteine is the only common L-amino acid with S configuration. This is solely due to the rules of the naming system: the carbon of the side chain - which is directly bonded to a sulfur - has higher priority than the carboxylate carbon. In the other 19 amino acids, the carboxylate carbon has priority #2, and the side chain carbon has priority #3.
E3.17:
a) Starting with the RRR stereoisomer (which is given in the example), we flip the first and third chiral center to get SRS. The enantiomer of the SRS stereoisomer is that in which all three chiral centers are flipped: the RSR stereoismer.

b) Epimers of the SRS stereoismer are RRS, SSS, and SRR (in each case, one of the three chiral centers has been flipped)
c) How to find the compounds that are diastereomers of the SRS stereoisomer, but not epimers? Start with the list of the eight possible stereoisomers given in the example. Cross out SRS itself, and its enantiomer RSR (determined in part (a) above). Then cross out the three epimers we found in part (b). We are left with three isomers: RRR, SSR, and RSS. Each of these have one chiral center in common with SRS, and two that are flipped.
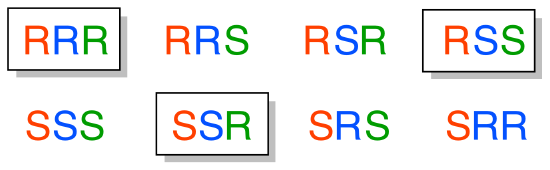
E3.18: This is the SRR stereoisomer:

E3.19:
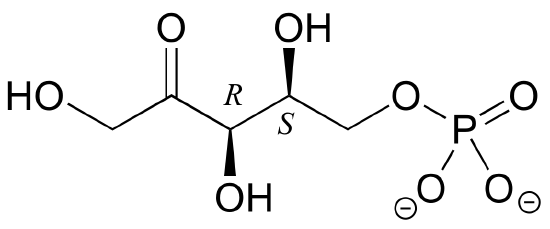
E3.20:
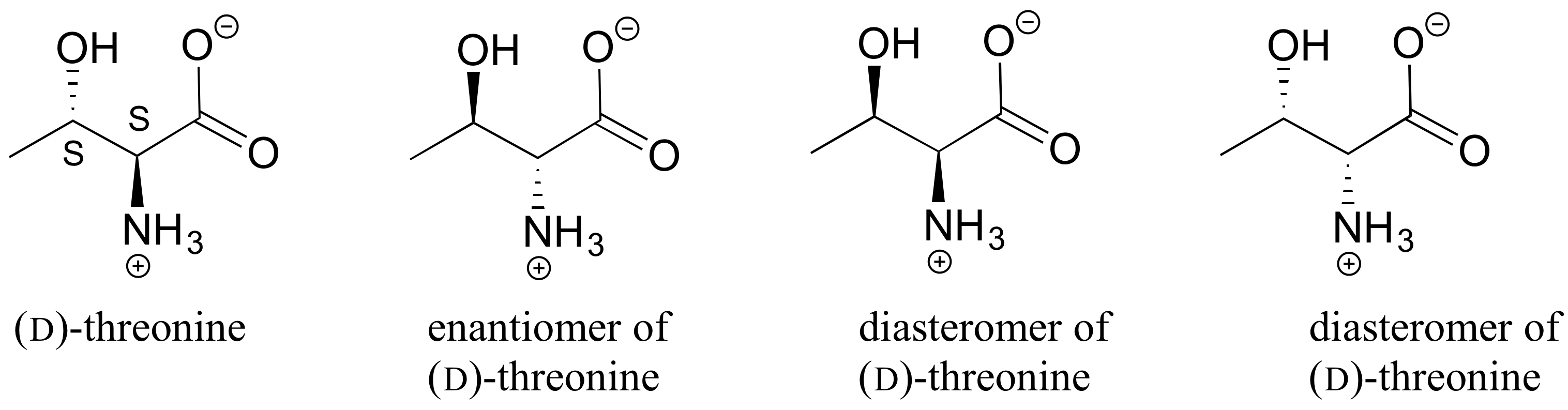
E3.21: Going left to right, top to bottom:
Diastereomers (two chiral centers are flipped).
Enantiomers (all five chiral centers are flipped).
Identical (drawing is flipped vertically but they are the same structure).
Identical (the carbon which appears to be flipped in the drawing is not a chiral center).
Constitutional isomers (same molecular formula, but notice that inositol does not have a ring oxygen. Is not a monosaccharide, it is a cyclohexane with six hydroxyl substituents.)
E3.22:
a) Identical. They have the same molecular formula and connectivity; there is only one chiral center, which is R in both structures.
b) Enantiomers. The compound on the left is R, compound on the right is S.
c) Enantiomers. The compound on the left is R, compound on the right is S.
d) Enantiomers. The compound on the left is SS, compound on the right is RR.
e) Identical. The structures are both glycerol, which is not chiral (the left and right 'arms' are the same, so the middle carbon is not a chiral center)
f) Identical. Both structures are SS. Also, notice that if you rotate the right-side structure 120 degrees clockwise, it becomes exactly the same as the left-side structure.
E3.23:
a) Not meso b) Meso. c) Not meso
d) Meso e) Not meso f) Meso
E3.24:
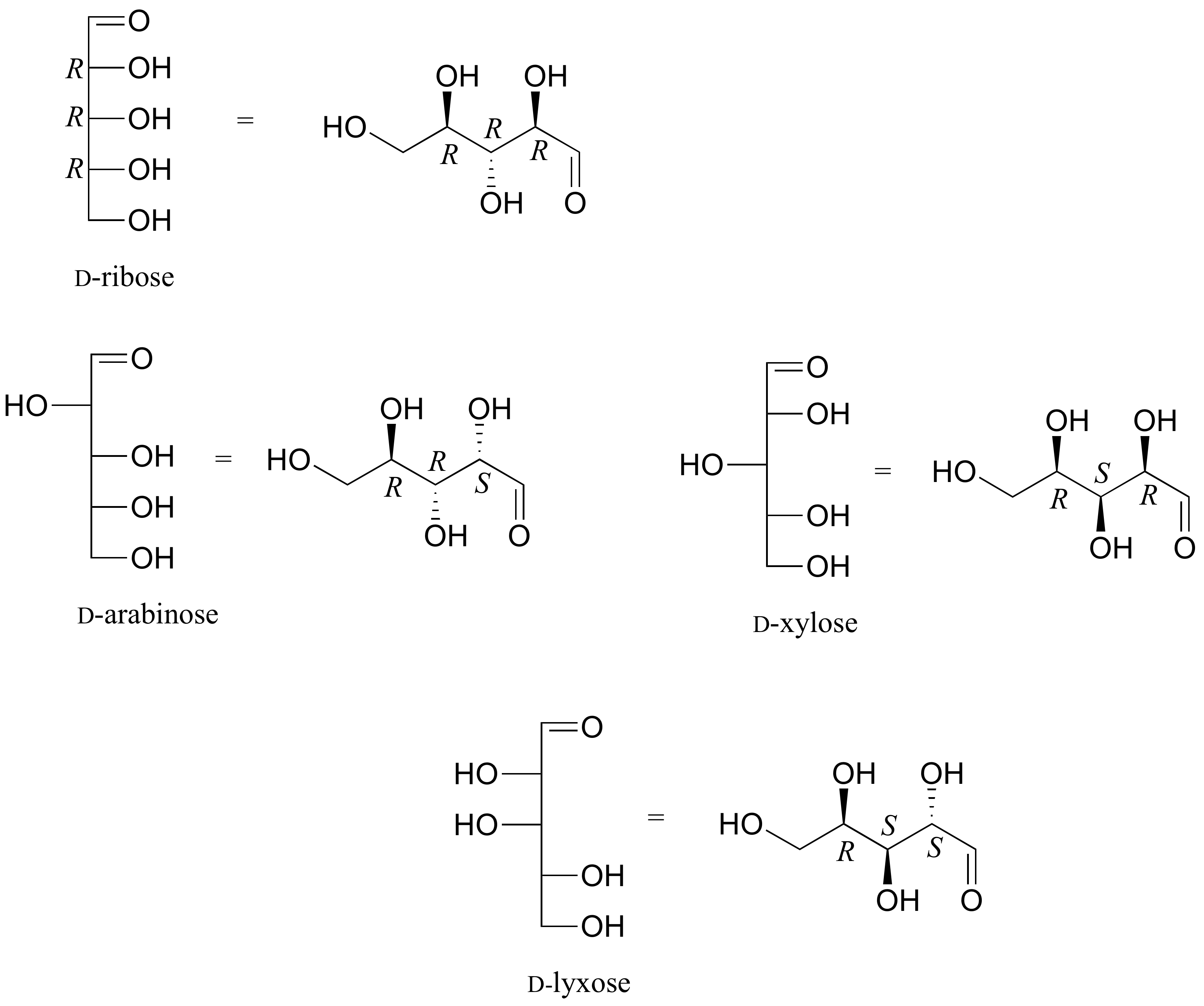
E3.25:
a) E b) N c) Z d) E
E3.26:
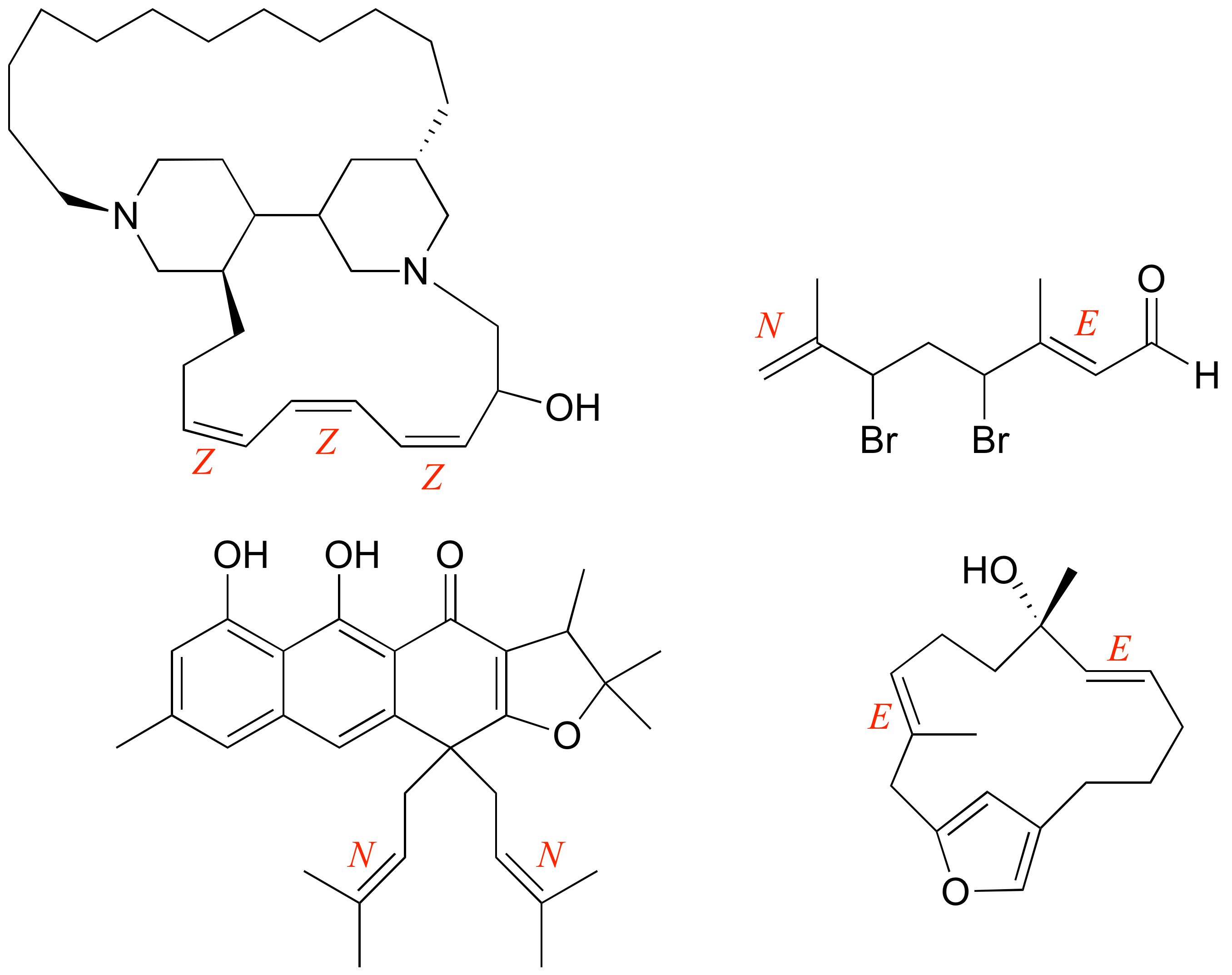
E3.27: The enantiomers of the compounds shown are below. Note that the chiral centers are flipped, but the stereogenic alkenes are not.

E3.28:
Ephedrine and pseudoephedrin are diastereomers (epimers). There are two chiral centers, and one of them (the OH) is flipped.
Methamphetamine and levo-methamphetamine are enantiomers (only one chiral center, and it is flipped). Methamphetamine technically should be called dextro-methamphetamine.
E3.29:
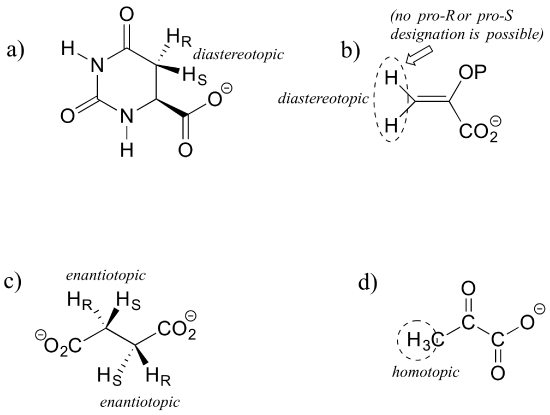
E3.30:
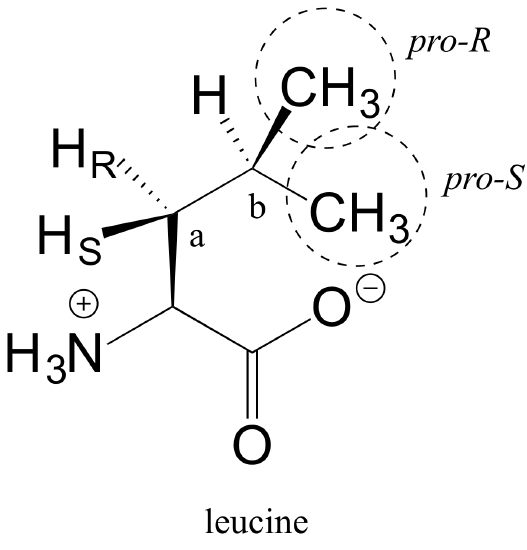
E3.31:



