Extra Credit 29

Question 17.4.2

For the \(\Delta G^{_{\circ}}\) values given here, determine the standard cell potential for the cell.

1. \(12 \frac{kJ}{mol}\), \(n=3\)
2. \(-45 \frac{kJ}{mol}\), \(n=1\)

Solution 17.4.2

In both Parts A and B, we are given the \(\Delta G^{_{\circ}}\) value, which is called the Standard Gibbs Free Energy. Because we are asked for the Standard Cell Potential, we can use the following equation the relates the Standard Cell Potential and Standard Gibbs Free Energy:

\( \Delta G^{_{\circ}} = {-n}FE_{cell}^{_{\circ}}\)

In the above equation, \(n\) represents the moles of electrons and \(F\) represents Faraday's constant, which is \(9.64855\times 10^{4} \frac{C}{mol\ e^{-}}\), or \(96,486\times 10^{4} \frac{C}{mol\ e^{-}}\).

For Part A, we are given \(\Delta G^{_{\circ}} = 12 \frac{kJ}{mol}\) and \(n\). Since \(F\) is a constant, we have everything we need in the equation to solve for \(E_{cell}^{_{\circ}}\). Now, we can simply plug this value into the equation above:

\( \Delta G^{_{\circ}} = {-n}FE_{cell}^{_{\circ}}\)

\((12 \frac{kJ}{mol}) = {(-3\ mol\ e^{-}})(9.64855\times 10^{4} \frac{C}{mol\ e^{-}})(E_{cell}^{_{\circ}})\)

Divide both sides by \({(-3\ mol\ e^{-}})(9.64855\times 10^{4} \frac{C}{mol\ e^{-}})\) to isolate \(E_{cell}^{_{\circ}}\).

\(\frac{(12 \frac{kJ}{mol})}{(-3\ mol\ e^{-})(9.64855\times 10^{4} \frac{C}{mol\ e^{-}})}= (E_{cell}^{_{\circ}})\)

Simplify

\((-4.14570065\times 10^{-5}\ \frac{kJ}{mol\ C})= (E_{cell}^{_{\circ}})\)

Convert units from \(\frac{kJ}{mol\ C}\) to \(V\). Start by converting \(kJ\) to \(J\) using the conversion \(1 kJ = 1000 J\).

\((-4.14570065\times 10^{-5}\ \frac{kJ}{mol\ C})(\frac{1000 J}{1 kJ})= (E_{cell}^{_{\circ}})\)

\((-0.0414570065 \frac{J}{mol\ C})= (E_{cell}^{_{\circ}})\)

Convert units to \(V\) using the conversion \(1\ V = \frac{J}{C}\), which gives us our \((E_{cell}^{_{\circ}})\)

\((-0.0414570065\ V)= (E_{cell}^{_{\circ}})\)

For Part B, we are given \(\Delta G^{_{\circ}} = -45 \frac{kJ}{mol}\) and \(n\). Since \(F\) is a constant, we have everything we need in the equation to solve for \(E_{cell}^{_{\circ}}\). Now, we can simply plug this value into the equation above:

\( \Delta G^{_{\circ}} = {-n}FE_{cell}^{_{\circ}}\)

\((-45 \frac{kJ}{mol}) = {(-1\ mol\ e^{-}})(9.64855\times 10^{4} \frac{C}{mol\ e^{-}})(E_{cell}^{_{\circ}})\)

Divide both sides by \({(-1\ mol\ e^{-}})(9.64855\times 10^{4} \frac{C}{mol\ e^{-}})\) to isolate \(E_{cell}^{_{\circ}}\).

\(\frac{(-45 \frac{kJ}{mol})}{(-1\ mol\ e^{-})(9.64855\times 10^{4} \frac{C}{mol\ e^{-}})}= (E_{cell}^{_{\circ}})\)

Simplify

\((4.66391323\times 10^{-4}\ \frac{kJ}{mol\ C})= (E_{cell}^{_{\circ}})\)

Convert units from \(\frac{kJ}{mol\ C}\) to \(V\). Start by converting \(kJ\) to \(J\) using the conversion \(1 kJ = 1000 J\).

\((4.66391323\times 10^{-4}\ \frac{kJ}{mol\ C})(\frac{1000 J}{1 kJ})= (E_{cell}^{_{\circ}})\)

\((0.466391323 \frac{J}{mol\ C})= (E_{cell}^{_{\circ}})\)

Convert units tox \(V\) using the conversion \(1\ V = \frac{J}{C}\), which gives us our \((E_{cell}^{_{\circ}})\)

\((0.466391323\ V)= (E_{cell}^{_{\circ}})\)

Thus, our answers when rounded to two significant figures are

a. \((-0.041\ V)= (E_{cell}^{_{\circ}})\)

b. \((0.47\ V)= (E_{cell}^{_{\circ}})\)

Question 12.1.2

Ozone decomposes to oxygen according to the equation \(2O_{3}(g) \rightarrow 3O_{2}(g)\). Write the equation that relates the rate expressions for this reaction in terms of the disappearance of \(O_{3}\) and the formation of oxygen.

Solution 12.1.2

Before breaking down the problem, it is important to understand what a rate expression is. Given a reaction \(aA + bB \rightarrow cC + dD\), the rate law would be \(rate=k[A]^{a}[B]^{b}\). This indicates that it is dependent on the concentration of reactants rather than on the products and that the coefficients (stoichiometry) does not determine anything rate-related (except in elementary reactions). There is also a rate constant, \(k\), which can be determined experimentally. The rate expression relates the decrease in concentration of reactants over time to the increase in concentration of products over time. Also keep in mind that since the reactant is disappearing, there is a negative sign in front of the rate expression. Also, remember to divide each expression by its corresponding stoichiometric coefficient.

\(rate = -\frac{\Delta [Reactant]}{\Delta t} = \frac{\Delta [Product]}{\Delta t}\)

For this problem, we are analyzing the rate expression with relation to the DISAPPEARANCE of \(O_{3}\) and the FORMATION of oxygen. "Disappearance" of \(O_{3}\)" indicates that \(O_{3}\) is the reactant in this reaction, so we would care about the concentration of \(O_{3}\), disregarding \(O_{2}\).

\(2O_{3}(g) \rightarrow 3O_{2}(g)\)

In this reaction \(O_{3}\) is a reactant and is disappearing, while \(O_{2}\) is a product and is being formed. Therefore, just plug in these values into the rate expression relationship above, and divide each by its stoichiometric coefficient. \(O_{3}\) has a coefficient of 2 so divide by 2, while \(O_{2}\) has a coefficient of 3 so divide its rate by 3.

\(rate = -\frac{\Delta [O_{3}]}{2 \Delta t} = \frac{\Delta [O_{2}]}{3 \Delta t}\)

Therefore, the \(rate=k[O_{3}]^{m}\). \(k\) can only be determined experimentally, so we do not have any information provided to find \(k\). Additionally, \(m\) cannot be determined either. We can only determine \(m\) experimentally (through order of a reaction) or through its coefficient. However, the coefficient of the reaction would be \(m\) only in an elementary reaction. Because the problem did not state that this is an elementary reaction, we must assume that it is a one step reaction. Thus, we cannot determine \(k\) or \(m\), leaving us with \(rate=k[O_{3}]^{m}\).

Question 12.4.20

For the past 10 years, the unsaturated hydrocarbon 1,3-butadiene (\(CH_{2}=CH=CH=CH_{2}\)) has ranked 38^th among the top 50 industrial chemicals. It is used primarily for the manufacture of synthetic rubber. An isomer exists also as cyclobutene:

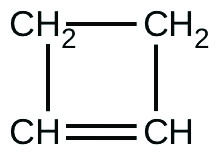
The isomerization of cyclobutene to butadiene is first-order and the rate constant has been measured as \(2.0\times 10^{-4}\ s^{-1}\) at \(150^{_{\circ}}\) in a \(0.53 L\) flask. Determine the partial pressure of cyclobutene and its concentration after \(30\) minutes if an isomerization reaction is carried out at \(150^{_{\circ}}\) with an initial pressure of \(55\) torr.

Solution 12.4.20

This problem is a multi-step problem that requires two answers: the concentration and partial pressure after \(30\) minutes. Although it seems like it'll be a difficult problem to tackle, breaking it into smaller steps will be more beneficial.

First, we can see and list out what we are given:

• \(k\ =\ 2.0\times 10^{-4}\ s^{-1}\)
• \(T\ =\ 150^{_{\circ}} C\)
• \(V\ =\ 0.53 L\)
• \(t\ =\ 30\ minutes\)
• \(P_{i}\ =\ 55\ torr\)

Now that we see what we are given and what we need, we can determine what steps to take. We need to use the Ideal Gas Law and the integrated rate law for first-order reactions. Since the integrated rate law require an initial concentration, we need to determine the initial concentration using the Ideal Gas Law.

In order to use the Ideal Gas Law, we have to make sure that everything is in the correct units. Let's start by converting all the units we have to the ones we need.

• \(T\ =\ 150^{_{\circ}}\ +\ 273.15\ =\ 423.15\ K\)
• \(V\ =\ 0.53\ L\)
• \(t\ =\ 30\ minutes\ \times\ \frac{60\ sec}{1\ min}\ =\ 1800\ seconds\)
• \(P_{i}\ =\ 55 torr\ \times\ \frac{1\ atm}{760\ torr}\ = 0.0723684211\ atm\)

Now we have our units in order, so we can begin plugging everything in. We know that we need to find an initial concentration for the integrated rate law, so let's start by finding concentration using the Ideal Gas Law. Assume no volume change because the problem does not state otherwise.

\(PV\ =\ nRT\)

\((0.0723684\ atm)(0.53\ L)\ =\ nR(423.15\ K)\)

As seen above, we only have our concentration and \(R\) left, where \(R\) is a gas constant that can change depending on units. Because of the units we're using, we are going to say \(R\ =\ 0.082057\ L^{-1}\ atm\ mol^{-1}\ K^{-1}\)

\((0.0723684\ atm)(0.53\ L)\ =\ n(0.082057\ L^{-1}\ atm\ mol_{-1}\ K^{-1})(423.15\ K)\)

Solving for \(n\) gives us an initial concentration of \(0.00110468\ mol\).

In this problem, we are told that this is a first-order reaction and we are given the rate constant, \(k\). Thus, we can use the integrated rate law for first-order reactions: \([A] = [A_{0}]e^{-kt}\).

We are already given every variable except \([A]\), which we are trying to solve for. Now, all we have to do is plug in the values we have.

\([A] = [A_{0}]e^{-kt}\)

\([A] = [0.00110468\ mol]e^{-(2.0\times 10^{-4}\ s^{-1})(1800\ s)}\)

\([A] = 7.707090839\times 10^{-4}\ mol\)

Everything has been completed now except for the final partial pressure, so now we can jump back to the Ideal Gas Law and plug in our \(n\) value to find \(P\).

\(PV\ =\ nRT\)

Again, the problem does not state that the volume changes, so assume no volume change.

\((P)(0.53\ L)\ =\ (7.707090839\times 10^{-4}\ mol)(0.082057\ L^{-1}\ atm\ mol_{-1}\ K^{-1})(423.15\ K)\)

\(P\ =\ 0.050489650120021\ atm\)

We finally have our answers now! All we have to do is adjust significant digits, which gives us

Concentration: \(7.7 \times 10^{-4}\ mol\)

Partial Pressure: \(0.050\ atm\)

Question 21.3.4

Complete each of the following equations:

1. \(\ce{^{7}_{3}Li}\ +\ ?\ \rightarrow\ 2\ce{^{4}_{2}He}\)
2. \(\ce{^{14}_{6}C}\ \rightarrow\ \ce{^{14}_{7}N}+\ ? \)
3. \(\ce{^{27}_{13}Al}\ +\ \ce{^{4}_{2}He}\ \rightarrow\ ?\ +\ \ce{^{1}_{0}n}\)
4. \(\ce{^{250}_{96}Cm}\ \rightarrow\ ?\ +\ \ce{^{98}_{38}Sr}\ +\ 4\ce{^{1}_{0}n}\)

Solution 21.3.4

1. Given the chemical equation \(\ce{^{7}_{3}Li}\ +\ ?\ \rightarrow\ 2\ce{^{4}_{2}He}\), we are going to treat \(?\) as a variable in the form \(\ce{^{X}_{Y}Z}\). This can let us make an equation to solve for the variables \(X\), \(Y\), and \(Z\). We want all the mass numbers (the top left number) to be equal on both sides, so we can say \(7\ +\ X\ = 2(4)\), and solving for \(X\) gives us \(X=1\). Similarly, solving for \(Y\) in the equation \(3\ +\ Y\ = 2(2)\) gives us \(Y=1\), resulting in \(\ce{^{1}_{1}Z}\). Since \(Z\) must have one proton (as denoted by \(Y\)), we can conclude that \(?\) is \(\ce{^{1}_{1}H}\).
2. Given the chemical equation \(\ce{^{14}_{6}C}\ \rightarrow\ \ce{^{14}_{7}N}+\ ? \), we are going to treat \(?\) as a variable in the form \(\ce{^{X}_{Y}Z}\). This can let us make an equation to solve for the variables \(X\), \(Y\), and \(Z\). We want all the mass numbers (the top left number) to be equal on both sides, so we can say \(14\ = 14\ +\ X\), and solving for \(X\) gives us \(X=0\). Similarly, solving for \(Y\) in the equation \(6\ = 7\ +\ Y\) gives us \(Y=-1\), resulting in \(\ce{^{0}_{-1}Z}\). Since \(Z\) must have one proton (as denoted by \(Y\)), we can conclude that \(?\) is \(\ce{^{0}_{-1}{\beta}}\). The reason we denote this particular example with \(\ce{^{0}_{-1}{\beta}}\) instead of \(\ce{^{0}_{-1}e}\) is because the "electron" is coming from the nucleus rather than acting as an electron in the surrounding orbitals. If it was an example of electron capture, we would say \(\ce{^{0}_{-1}e}\) in place of \(\ce{^{0}_{-1}{\beta}}\). Essentially, the difference is what kind of electron - from the nucleus or in the surrounding space.
3. Given the chemical equation \(\ce{^{27}_{13}Al}\ +\ \ce{^{4}_{2}He}\ \rightarrow\ ?\ +\ \ce{^{1}_{0}n}\), we are going to treat \(?\) as a variable in the form \(\ce{^{X}_{Y}Z}\). This can let us make an equation to solve for the variables \(X\), \(Y\), and \(Z\). We want all the mass numbers to be equal on both sides, so we can say \(27\ +\ 4\ = X\ +\ 1\), and solving for \(X\) gives us \(X=30\). Similarly, solving for \(Y\) in the equation \(13\ +\ 2\ = Y\ +\ 0\) gives us \(Y=15\), resulting in \(\ce{^{30}_{15}Z}\). Since \(Z\) must have fifteen protons (as denoted by \(Y\)), we can conclude that \(?\) is \(\ce{^{30}_{15}P}\).
4. Given the chemical equation \(\ce{^{250}_{96}Cm}\ \rightarrow\ ?\ +\ \ce{^{98}_{38}Sr}\ +\ 4\ce{^{1}_{0}n}\), we are going to treat \(?\) as a variable in the form \(\ce{^{X}_{Y}Z}\). This can let us make an equation to solve for the variables \(X\), \(Y\), and \(Z\). We want all the mass numbers to be equal on both sides, so we can say \(250\ = X\ +\ 98\ + 4(1)\), and solving for \(X\) gives us \(X=148\). Similarly, solving for \(Y\) in the equation \(96\ = Y\ +\ 38\ +\ 0\) gives us \(Y=58\), resulting in \(\ce{^{148}_{58}Z}\). Since \(Z\) must have \(58\) protons (as denoted by \(Y\)), we can conclude that \(?\) is \(\ce{^{148}_{58}Ce}\).

Question 20.1.1

Identify the oxidation state of the atoms in the following compounds:

1. \(PCl_3\)
2. \(CO_3^{2-}\)
3. \(H_2S\)
4. \(S_8\)
5. \(SCl_2\)
6. \(Na_2SO_3\)
7. \(SO_4^{2-}\)

Solution 20.1.1

First you need to look at the Oxidation State Rules, which will inform you of oxidation rules in order to assign oxidation numbers in certain orders.

1. Based on the Oxidation State Rules, Chlorine is a Halogen (Group 17 or 7A), so it must have an oxidation state of \(-1\). The overall charge of the molecule is \(0\) (neutral), so we can use an equation to find the oxidation state of \(P\). We multiply each charge of the atom by the number of that atom present, and then set it equal to the overall charge of the molecule. This gives the equation \(1(P) + 3(-1) = 0\). Solving this equation tells us that the oxidation state of \(P\) is \(+3\).
2. Based on the Oxidation State Rules, Oxygen has an oxidation state of \(-2\). The overall charge of the molecule is \(-2\), so we can use an equation to find the oxidation state of \(C\). We multiply each charge of the atom by the number of that atom present, and then set it equal to the overall charge of the molecule. This gives the equation \(1(C) + 3(-2) = -2\). Solving this equation tells us that the oxidation state of \(C\) is \(+4\).
3. Based on the Oxidation State Rules, Sulfur has an oxidation state of \(-2\). The overall charge of the molecule is \(0\), so we can use an equation to find the oxidation state of \(H\). We multiply each charge of the atom by the number of that atom present, and then set it equal to the overall charge of the molecule. This gives the equation \(2(H) + 1(-2) = 0\). Solving this equation tells us that the oxidation state of \(H\) is \(+1\).
4. Based on the Oxidation State Rules, Sulfur has an oxidation state of \(-2\). However, since it is in its elemental form and it is not bonded to other elements, it has an oxidation state of \(0\).
5. Based on the Oxidation State Rules, Sulfur has an oxidation state of \(-2\) and Chlorine has an oxidation state of \(-1\). However, the overall charge of the molecule is \(0\), which means that there is a conflict here. Because there is a conflict of rules, we must refer to the electronegativity of each atom. In this case, Chlorine is more electronegative than sulfur, so it would receive its assigned oxidation state of \(-1\). Now, we can use an equation to find the oxidation state of \(S\). We multiply each charge of the atom by the number of that atom present, and then set it equal to the overall charge of the molecule. This gives the equation \(1(S) + 2(-1) = 0\). Solving this equation tells us that the oxidation state of \(S\) is \(+2\).
6. Based on the Oxidation State Rules, Sodium has an oxidation state of \(+1\) and Oxygen has an oxidation state of \(-2\). The overall charge of the molecule is \(0\), so we can use an equation to find the oxidation state of \(S\). We multiply each charge of the atom by the number of that atom present, and then set it equal to the overall charge of the molecule. This gives the equation \(2(+1) + 1(S) + 3(-2) = 0\). Solving this equation tells us that the oxidation state of \(S\) is \(+4\).
7. Based on the Oxidation State Rules, Oxygen has an oxidation state of \(-2\). The overall charge of the molecule is \(-2\), so we can use an equation to find the oxidation state of \(S\). We multiply each charge of the atom by the number of that atom present, and then set it equal to the overall charge of the molecule. This gives the equation \(1(S) + 4(-2) = -2\). Solving this equation tells us that the oxidation state of \(S\) is \(+6\).

Question 20.4.19

Carbon is used to reduce iron ore to metallic iron. The overall reaction is as follows:

\[2Fe_{2}O_{3} \cdot xH_{2}O(s) + 3C(s) \rightarrow 4Fe(l)+3CO_{2}(g) + 2xH_{2}O(g)\]

Write the two half-reactions for this overall reaction.

Solution 20.4.19

Before splitting the half-reactions, it is essential to understand what each half-reaction means. One half-reaction represents the oxidation reaction, while the other represents the reduction reaction. The best way to differentiate is by remembering OIL RIG, which means Oxidation Is Loss (of electrons) and Reduction Is Gain (of electrons). Thus, if the oxidation number of a compound increases, then we know it is losing electrons, so it is being oxidized. Similarly, if the oxidation number of a compound decreases, then it is gaining electrons, so it is being reduced. For this example, we can analyze each of the oxidation numbers for each atom to see how they change.

• The \(Fe\) in \(Fe_{2}O_{3}\) has an oxidation number of \(+3\)
• The \(O\) in \(Fe_{2}O_{3}\) has an oxidation number of \(-2\)
• The \(H\) in \(H_{2}O\) has an oxidation number of \(+1\)
• The \(O\) in \(H_{2}O\) has an oxidation number of \(-2\)
• The \(C\) has an oxidation number of \(0\)
• The \(Fe\) has an oxidation number of \(0\)
• The \(C\) in \(CO_{2}\) has an oxidation number of \(+4\)
• The \(O\) in \(CO_{2}\) has an oxidation number of \(-2\)
• The \(H\) in \(H_{2}O\) has an oxidation number of \(+1\)
• The \(O\) in \(H_{2}O\) has an oxidation number of \(-2\)

From this, we can determine that the oxidation state of \(Fe\) goes from \(+3\) to \(0\), so it is gains electrons and is reduced. Additionally, the oxidation state of \(C\) goes from \(0\) to \(+4\), so it loses electrons and is oxidized. Now that we have broken down and classified what agents are being oxidized and reduced, we can write the half-reactions.

Oxidation: \(3C\ \rightarrow\ 3CO_{2}\)

Reduction: \(2Fe_{2}O_{3} \cdot H_{2}O\ \rightarrow\ 4Fe\ +\ 2H_{2}O\)

However, if you look at the reactions, they are not balanced on their own. Because it does not state that it is in an acidic or basic solution, we will assume that it is in an acidic solution. Therefore, we must follow the rules to balancing redox reactions.

Let's start by looking at the oxidation half-reaction: \(3C(s)\ \rightarrow\ 3CO_{2}(g)\). By looking at this, we see that we have \(6O\) on the product side, so we can balance this by adding \(6H_{2}O\) on the other side.

\(3C\ +\ 6H_{2}O\ \rightarrow\ 3CO_{2}\)

Now our \(O\) is balanced, but we have \(12H\) on the reactant side, so we add \(12H^{+}\) to the products' side to balance this out.

\(3C\ +\ 6H_{2}O\ \rightarrow\ 3CO_{2}\ +\ 12H^{+}\)

We're almost done now! The last step is to balance the charges. Since we have \(0\ \rightarrow\ 12\), we need to add a \(-12\) to the products' side as well. We do this in the form of electrons. This gives us the final, balanced oxidation half-reaction.

\(3C\ +\ 6H_{2}O\ \rightarrow\ 3CO_{2}\ +\ 12H^{+}\ +\ 12e^{-}\)

Now let's look at the reduction half-reaction: \(2Fe_{2}O_{3} \cdot H_{2}O\ \rightarrow\ 4Fe\ +\ 2H_{2}O\). By looking at this, we see that we have \(2H\) on the reactant side, but \(4\) on the product side. There is also a mismatched amount of \(O\) - we have \(7O\) on the reactant side and \(2O\) on the product side. We can start by trying to balance the \(O\).

First, we can add \(7H_{2}O\) to the product side and \(2H_{2}O\) to the reactant side.

\(2Fe_{2}O_{3} \cdot H_{2}O\ +\ 2H_{2}O\ \rightarrow\ 4Fe\ +\ 2H_{2}O\ +\ 7H_{2}O\)

The \(2H_{2}O\) on both sides cancels out, leaving us with the following reaction:

\(2Fe_{2}O_{3} \cdot H_{2}O\ \rightarrow\ 4Fe\ +\ 7H_{2}O\)

Now our \(O\) is balanced, but we have \(2H\) on the reactant side and \(14H\) on the product side, so we add \(12H^{+}\) to the reactants' side to balance this out.

\(2Fe_{2}O_{3} \cdot H_{2}O\ +\ 12H^{+}\ \rightarrow\ 4Fe\ +\ 7H_{2}O\)

We're almost done now! The last step is to balance the charges. Since we have \(12\ \rightarrow\ 0\), we need to add a \(-12\) to the reactants' side as well. We do this in the form of electrons. This gives us the final, balanced oxidation half-reaction.

\(2Fe_{2}O_{3} \cdot H_{2}O\ +\ 12H^{+}\ +\ 12e^{-}\ \rightarrow\ 4Fe\ +\ 7H_{2}O\)

Now that we have the two half-reactions, we can double-check to make sure that we get the overall reaction when they are added.

\(3C\ +\ 6H_{2}O\ \rightarrow\ 3CO_{2}\ +\ 12H^{+}\ +\ 12e^{-}\)

\(2Fe_{2}O_{3} \cdot H_{2}O\ +\ 12H^{+}\ +\ 12e^{-}\ \rightarrow\ 4Fe\ +\ 7H_{2}O\)

Notice that the \(12H^{+}\) and \(12e^{-}\) cancel out on both sides and the equation matches the original equation.

Since the reactions, when added, yield the original reaction, we can confirm that the following reactions are the half-reactions for this redox reaction:

Oxidation: \(3C\ +\ 6H_{2}O\ \rightarrow\ 3CO_{2}\ +\ 12H^{+}\ +\ 12e^{-}\)

Reduction: \(2Fe_{2}O_{3} \cdot H_{2}O\ +\ 12H^{+}\ +\ 12e^{-}\ \rightarrow\ 4Fe\ +\ 7H_{2}O\)

Question 20.9.4

Two solutions, one containing \(Fe(NO_{3})_{2} \cdot 6H_{2}O\) and the other containing the same molar concentration of \(Fe(NO_{3})_{3} \cdot 6H_{2}O\), were electrolyzed under identical conditions. Which solution produced the most metal? Justify your answer.

Solution 20.9.4

The problem states that all conditions are identical. Thus, the only difference in \(Fe(NO_{3})_{2} \cdot 6H_{2}O\) and \(Fe(NO_{3})_{3} \cdot 6H_{2}O\) is the number of \(NO_{3}\) molecules present. This is a case of electrolysis, which is the process of causing nonspontaneous reactions to occur. Thus, looking at the number of \(NO_{3}\) molecules is important. Given that it isn't a spontaneous reaction, would it be easier to "take off" three \(NO_{3}\) molecules or two \(NO_{3}\) molecules? In order to break these bonds, energy is required, so it would be easier (require less energy) to break two of the bonds than three of those same bonds. Since both molecules undergo identical electrolysis, the molecule whose bonds are easier to break will produce the most product. Therefore, since \(Fe(NO_{3})_{2} \cdot 6H_{2}O\) is more likely to break apart than \(Fe(NO_{3})_{3} \cdot 6H_{2}O\), meaning that the \(Fe(NO_{3})_{2} \cdot 6H_{2}O\) would produce the most metal.

Question 20.8.3

Why is it important for automobile manufacturers to apply paint to the metal surface of a car? Why is this process particularly important for vehicles in northern climates, where salt is used on icy roads?

Solution 20.8.3

Painting a surface of a car helps prevent corrosion. Corrosion is a term used to describe the breaking down, or deterioration, of metals that occurs as a result of redox reactions. In the case of car corrosion, the primary concern is rust, which forms using the following redox equation:

\(4Fe\ +\ 3O_{2}\ +\ 6H_{2}O\ \rightarrow\ 4Fe(OH)_{3}\)

Essentially, the iron is losing electrons to oxygen. Salt (an electrolyte) increases the conductivity of water and concentration of ions in that water, subsequently increasing the rate of corrosion (oxidation of the metal).

It is important for automobile manufacturers to apply paint to the metal surface of a car because it serves as a form of prophylactic protection to prevent corrosion of the car metal. The paint itself prevents substances, such as water and oxygen, from directly contacting the metal on the car, preventing oxidation of the metal from occurring.

This process is particularly important for vehicles in northern climates because the salt used on roads can act as an electrolyte (agent for electrolysis). As explained above, introducing a mixture of salt and water to the car accelerates the rate of corrosion by increasing the rate of the oxidation reaction. Therefore, it is even more important to ensure that the paint on the car is properly applied.