25.3: Colligative Properties Depend only on Number Density
- Page ID
- 14515
Colligative properties are important properties of solutions as they describe how the properties of the solvent will change as solute (or solutes) is (are) added. Before discussing these important properties, let us first review some definitions.
- Solution – a homogeneous mixture.
- Solvent – The component of a solution with the largest mole fraction
- Solute – Any component of a solution that is not the solvent.
Solutions can exist in solid (alloys of metals are an example of solid-phase solutions), liquid, or gaseous (aerosols are examples of gas-phase solutions) forms. For the most part, this discussion will focus on liquid-phase solutions.
Freezing Point Depression
In general (and as will be discussed in Chapter 8 in more detail) a liquid will freeze when
\[ \mu_{solid} \le \mu_{liquid} \nonumber \]
As such, the freezing point of the solvent in a solution will be affected by anything that changes the chemical potential of the solvent. As it turns out, the chemical potential of the solvent is reduced by the presence of a solute.
In a mixture, the chemical potential of component \(A\) can be calculated by
\[\mu_A=\mu_A^o + RT \ln \chi_A \label{chemp} \]
And because \(\chi_A\) is always less than (or equal to) 1, the chemical potential is always reduced by the addition of another component.
The condition under which the solvent will freeze is
\[ \mu_{A,solid} = \mu_{A,liquid} \nonumber \]
where the chemical potential of the liquid is given by Equation \ref{chemp}, which rearrangement to
\[\dfrac{ \mu_A -\mu_A^o}{RT} = \ln \chi_A \nonumber \]
To evaluate the temperature dependence of the chemical potential, it is useful to consider the temperature derivative at constant pressure.
\[ \left[ \dfrac{\partial}{\partial T} \left( \dfrac{\mu_A-\mu_A^o}{RT} \right) \right]_{p} = \left( \dfrac{\partial \ln \chi_A}{\partial T} \right)_p \nonumber \]
\[- \dfrac{\mu_A - \mu_A^o}{RT^2} + \dfrac{1}{RT} \left[ \left( \dfrac{\partial \mu_A}{\partial T} \right)_p -\left( \dfrac{\partial \mu_A^o}{\partial T} \right)_p \right] =\left( \dfrac{\partial \ln \chi_A}{\partial T} \right)_p \label{bigeq} \]
Recalling that
\[ \mu = H = TS \nonumber \]
and
\[\left( \dfrac{\partial \mu}{\partial T} \right)_p =-S \nonumber \]
Equation \ref{bigeq} becomes
\[ - \dfrac{(H_A -TS_A - H_A^o + TS^o_A)}{RT^2} + \dfrac{1}{RT} \left[ -S_A + S_A^o\right] =\left( \dfrac{\partial \ln \chi_A}{\partial T} \right)_p \label{bigeq2} \]
And noting that in the case of the solvent freezing, \(H_A^o\) is the enthalpy of the pure solvent in solid form, and \(H_A\) is the enthalpy of the solvent in the liquid solution. So
\[ H_A^o - H_a = \Delta H_{fus} \nonumber \]
Equation \ref{bigeq2} then becomes
\[ \dfrac{\Delta H_{fus}}{RT^2} - \cancel{ \dfrac{-S_A + S_A^o}{RT}} + \cancel{\dfrac{-S_A + S_A^o}{RT}}=\left( \dfrac{\partial \ln \chi_A}{\partial T} \right)_p \nonumber \]
or
\[ \dfrac{\Delta H_{fus}}{RT^2} = \left( \dfrac{\partial \ln \chi_A}{\partial T} \right)_p \nonumber \]
Separating the variables puts the equation into an integrable form.
\[ \int_{T^o}^T \dfrac{\Delta H_{fus}}{RT^2} dT = \int d \ln \chi_A \label{int1} \]
where \(T^{o}\) is the freezing point of the pure solvent and \(T\) is the temperature at which the solvent will begin to solidify in the solution. After integration of Equation \ref{int1}:
\[ - \dfrac{\Delta H_{fus}}{R} \left( \dfrac{1}{T} - \dfrac{1}{T^{o}} \right) = \ln \chi_A \label{int3} \]
This can be simplified further by noting that
\[ \dfrac{1}{T} - \dfrac{1}{T^o} = \dfrac{T^o - T}{TT^o} = \dfrac{\Delta T}{TT^o} \nonumber \]
where \(\Delta T\) is the difference between the freezing temperature of the pure solvent and that of the solvent in the solution. Also, for small deviations from the pure freezing point, \(TT^o\) can be replaced by the approximate value \((T^o)^2\). So the Equation \ref{int3} becomes
\[ - \dfrac{\Delta H_{fus}}{R(T^o)^2} \Delta T = \ln \chi_A \label{int4} \]
Further, for dilute solutions, for which \(\chi_A\), the mole fraction of the solvent is very nearly 1, then
\[ \ln \chi_A \approx -(1 -\chi_A) = -\chi_B \nonumber \]
where \(\chi_B\) is the mole fraction of the solute. After a small bit of rearrangement, this results in an expression for freezing point depression of
\[ \Delta T = \left( \dfrac{R(T^o)^2}{\Delta H_{fus}} \right) \chi_B \nonumber \]
The first factor can be replaced by \(K_f\):
\[\dfrac{R(T^o)^2}{\Delta H_{fus}} = K_f \nonumber \]
which is the cryoscopic constant for the solvent.
\(\Delta T\) gives the magnitude of the reduction of freezing point for the solution. Since \(\Delta H_{fus}\) and \(T^o\) are properties of the solvent, the freezing point depression property is independent of the solute and is a property based solely on the nature of the solvent. Further, since \(\chi_B\) was introduced as \((1 - \chi_A)\), it represents the sum of the mole fractions of all solutes present in the solution.
It is important to keep in mind that for a real solution, freezing of the solvent changes the composition of the solution by decreasing the mole fraction of the solvent and increasing that of the solute. As such, the magnitude of \(\Delta T\) will change as the freezing process continually removes solvent from the liquid phase of the solution.
Boiling Point Elevation
The derivation of an expression describing boiling point elevation is similar to that for freezing point depression. In short, the introduction of a solute into a liquid solvent lowers the chemical potential of the solvent, cause it to favor the liquid phase over the vapor phase. As sch, the temperature must be increased to increase the chemical potential of the solvent in the liquid solution until it is equal to that of the vapor-phase solvent. The increase in the boiling point can be expressed as
\[ \Delta T = K_b \chi_B \nonumber \]
where
\[\dfrac{R(T^o)^2}{\Delta H_{vap}} = K_b \nonumber \]
is called the ebullioscopic constant and, like the cryoscopic constant, is a property of the solvent that is independent of the solute or solutes. A very elegant derivation of the form of the models for freezing point depression and boiling point elevation has been shared by F. E. Schubert (Schubert, 1983).
Cryoscopic and ebullioscopic constants are generally tabulated using molality as the unit of solute concentration rather than mole fraction. In this form, the equation for calculating the magnitude of the freezing point decrease or the boiling point increase is
\[ \Delta T = K_f \,m \nonumber \]
or
\[ \Delta T = K_b \,m \nonumber \]
where \(m\) is the concentration of the solute in moles per kg of solvent. Some values of \(K_f\) and \(K_b\) are shown in the table below.
| Substance | \(K_f\) (°C kg mol-1) | \(T^o_f\) (°C) | \(K_b\) (°C kg mol-1) | \(T^o_b\) (°C) |
|---|---|---|---|---|
| Water | 1.86 | 0.0 | 0.51 | 100.0 |
| Benzene | 5.12 | 5.5 | 2.53 | 80.1 |
| Ethanol | 1.99 | -114.6 | 1.22 | 78.4 |
| CCl4 | 29.8 | -22.3 | 5.02 | 76.8 |
The boiling point of a solution of 3.00 g of an unknown compound in 25.0 g of CCl4 raises the boiling point to 81.5 °C. What is the molar mass of the compound?
Solution
The approach here is to find the number of moles of solute in the solution. First, find the concentration of the solution:
\[(85.5\, °C- 76.8\, °C) = \left( 5.02\, °C\,Kg/mol \right) m \nonumber \]
\[ m= 0.936\, mol/kg \nonumber \]
Using the number of kg of solvent, one finds the number for moles of solute:
\[ \left( 0.936 \,mol/\cancel{kg} \right) (0.02\,\cancel{kg}) =0.0234 \, mol \nonumber \]
The ratio of mass to moles yields the final answer:
\[\dfrac{3.00 \,g}{0.0234} = 128 g/mol \nonumber \]
Vapor Pressure Lowering
For much the same reason as the lowering of freezing points and the elevation of boiling points for solvents into which a solute has been introduced, the vapor pressure of a volatile solvent will be decreased due to the introduction of a solute. The magnitude of this decrease can be quantified by examining the effect the solute has on the chemical potential of the solvent.
In order to establish equilibrium between the solvent in the solution and the solvent in the vapor phase above the solution, the chemical potentials of the two phases must be equal.
\[\mu_{vapor} = \mu_{solvent} \nonumber \]
If the solute is not volatile, the vapor will be pure, so (assuming ideal behavior)
\[\mu_{vap}^o + RT \ln \dfrac{p'}{p^o} = \mu_A^o + RT \ln \chi_A \label{eq3} \]
Where \(p’\) is the vapor pressure of the solvent over the solution. Similarly, for the pure solvent in equilibrium with its vapor
\[ \mu_A^o = \mu_{vap}^o + RT \ln \dfrac{p_A}{p^o} \label{eq4} \]
where \(p^o\) is the standard pressure of 1 atm, and \(p_A\) is the vapor pressure of the pure solvent. Substituting Equation \ref{eq4} into Equation \ref{eq3} yields
\[ \cancel{\mu_{vap}^o} + RT \ln \dfrac{p'}{p^o}= \left ( \cancel{\mu_{vap}^o} + RT \ln \dfrac{p_A}{p^o} \right) + RT \ln \chi_A \nonumber \]
The terms for \(\mu_{vap}^o\) cancel, leaving
\[ RT \ln \dfrac{p'}{p^o}= RT \ln \dfrac{p_A}{p^o} + RT \ln \chi_A \nonumber \]
Subtracting \(RT \ln(P_A/P^o)\) from both side produces
\[ RT \ln \dfrac{p'}{p^o} - RT \ln \dfrac{p_A}{p^o} = RT \ln \chi_A \nonumber \]
which rearranges to
\[RT \ln \dfrac{p'}{p_A} = RT \ln \chi_A \nonumber \]
Dividing both sides by \(RT\) and then exponentiating yields
\[ \dfrac{p'}{p_A} = \chi_A \nonumber \]
or
\[ p'=\chi_Ap_A \label{RL} \]
This last result is Raoult’s Law. A more formal derivation would use the fugacities of the vapor phases, but would look essentially the same. Also, as in the case of freezing point depression and boiling point elevations, this derivation did not rely on the nature of the solute! However, unlike freezing point depression and boiling point elevation, this derivation did not rely on the solute being dilute, so the result should apply the entire range of concentrations of the solution.
Consider a mixture of two volatile liquids A and B. The vapor pressure of pure A is 150 Torr at some temperature, and that of pure B is 300 Torr at the same temperature. What is the total vapor pressure above a mixture of these compounds with the mole fraction of B of 0.600. What is the mole fraction of B in the vapor that is in equilibrium with the liquid mixture?
Solution
Using Raoult’s Law (Equation \ref{RL})
\[ p_A = (0.400)(150\, Toor) =60.0 \,Torr \nonumber \]
\[ p_B = (0.600)(300\, Toor) =180.0 \,Torr \nonumber \]
\[ p_{tot} = p_A + p_B = 240 \,Torr \nonumber \]
To get the mole fractions in the gas phase, one can use Dalton’s Law of partial pressures.
\[ \chi_A = \dfrac{ p_A}{p_{tot}} = \dfrac{60.0 \,Torr}{240\,Torr} = 0.250 \nonumber \]
\[ \chi_B = \dfrac{ p_B}{p_{tot}} = \dfrac{180.0 \,Torr}{240\,Torr} = 0.750 \nonumber \]
And, of course, it is also useful to note that the sum of the mole fractions is 1 (as it must be!)
\[ \chi_A+\chi_B =1 \nonumber \]
Osmotic Pressure
Osmosis is a process by which solvent can pass through a semi-permeable membrane (a membrane through which solvent can pass, but not solute) from an area of low solute concentration to a region of high solute concentration. The osmotic pressure is the pressure that when exerted on the region of high solute concentration will halt the process of osmosis.
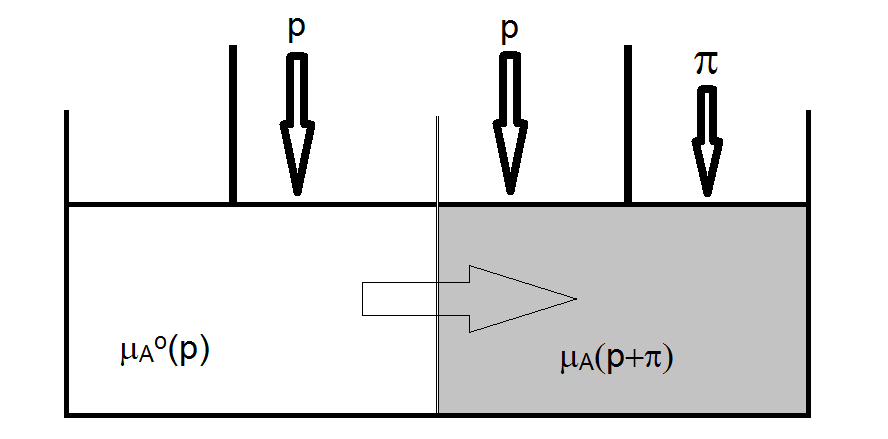
The nature of osmosis and the magnitude of the osmotic pressure can be understood by examining the chemical potential of a pure solvent and that of the solvent in a solution. The chemical potential of the solvent in the solution (before any extra pressure is applied) is given by
\[ \mu_A = \mu_A^o + RT \ln \chi_A \nonumber \]
And since xA < 1, the chemical potential is of the solvent in a solution is always lower than that of the pure solvent. So, to prevent osmosis from occurring, something needs to be done to raise the chemical potential of the solvent in the solution. This can be accomplished by applying pressure to the solution. Specifically, the process of osmosis will stop when the chemical potential solvent in the solution is increased to the point of being equal to that of the pure solvent. The criterion, therefore, for osmosis to cease is
\[ \mu_A^o(p) = \mu_A(\chi_b, +\pi) \nonumber \]
To solve the problem to determine the magnitude of p, the pressure dependence of the chemical potential is needed in addition to understanding the effect the solute has on lowering the chemical potential of the solvent in the solution. The magnitude, therefore, of the increase in chemical potential due to the application of excess pressure p must be equal to the magnitude of the reduction of chemical potential by the reduced mole fraction of the solvent in the solution. We already know that the chemical potential of the solvent in the solution is reduced by an amount given by
\[ \mu^o_A - \mu_A = RT \ln \chi_A \nonumber \]
And the increase in chemical potential due to the application of excess pressure is given by
\[ \mu(p+\pi) = \mu(p) + \int _{p}^{\pi} \left( \dfrac{\partial \mu}{\partial p} \right)_T dp \nonumber \]
The integrals on the right can be evaluated by recognizing
\[\left( \dfrac{\partial \mu}{\partial p} \right)_T = V \nonumber \]
where \(V\) is the molar volume of the substance. Combining these expressions results in
\[ -RT \ln \chi_A = \int_{p}^{p+\pi} V\,dp \nonumber \]
If the molar volume of the solvent is independent of pressure (has a very small value of \(\kappa_T\) – which is the case for most liquids) the term on the right becomes.
\[ \int_{p}^{\pi} V\,dP = \left. V p \right |_{p}^{p+\pi} = V\pi \nonumber \]
Also, for values of \(\chi_A\) very close to 1
\[ \ln \chi_A \approx -(1- \chi_A) = - \chi_B \nonumber \]
So, for dilute solutions
\[ \chi_B RT = V\pi \nonumber \]
Or after rearrangement
\[ \pi \dfrac{\chi_B RT}{V} \nonumber \]
again, where \(V\) is the molar volume of the solvent. And finally, since \(\chi_B/V\) is the concentration of the solute \(B\) for cases where \(n_B \ll n_A\). This allows one to write a simplified version of the expression which can be used in the case of very dilute solutions
\[ \pi = [B]RT \nonumber \]
When a pressure exceeding the osmotic pressure \(\pi\) is applied to the solution, the chemical potential of the solvent in the solution can be made to exceed that of the pure solvent on the other side of the membrane, causing reverse osmosis to occur. This is a very effective method, for example, for recovering pure water from a mixture such as a salt/water solution.
Colligative properties are properties that depend on the number of particles rather than their total mass. This implies that these properties can be used to measure molar mass. Colligative properties include:
- melting point depression
- boiling point elevation
- osmotic pressure
Melting Point Depression
When we freeze a dilute solution the resulting frozen solvent is often quite a bit purer than the original solution. Let us consider this problem and make the following rather opposite assumptions about the solvent component:
- In the liquid state it can be considered to follow Raoult's law over a sufficient concentration range
- In the solid state, the solubility is nil
Under these two assumptions, we can consider the thermodynamic potentials of the solvent component (1) at the freezing point. They should be equal once equilibrium has been reached:
\[μ_1^s = μ_1^{sln} \nonumber \]
\[μ_1^s = μ_1^{liq*} + RT\ln\, a_1 \nonumber \]
\[ \dfrac{μ_1^s - μ_1^{liq*} }{RT}=\ln \, a_1 \nonumber \]
\[ \dfrac{-Δμ_1}{RT}=\ln \,a_1 \nonumber \]
We can now apply Gibbs-Helmholtz relations by differentiation with respect to temperature:
\[ \dfrac{\partial}{\partial\;T} \dfrac{Δμ_1}{T} = \dfrac{- Δ_{fus}H_{molar,1}}{T^2} \nonumber \]
\[\dfrac{\partial [\ln\,a_1}{\partial T} = \dfrac{Δ_{fus}H_{molar,1}}{RT^2} \nonumber \]
This means that we can actually use the quantity \(Δ_{fus}H_{molar,1}/RT^2\) to determine activities by integration, but usually Raoult Law is assumed valid:
\[\ln a_1 \ln x_1 ≈ -x_2 \nonumber \]
If we integrate \(Δ_{fus}H_{molar,1}/RT^2\) from the melting point of the pure solvent \(T_m^*\) to the actual melting point of the solution \(T_m\) we get:
\[-x_2 = \dfrac{Δ_{fus}H_{molar,1}}{R} \left( \dfrac{1}{T_m^*}- \dfrac{1}{T_m} \right) = \dfrac{Δ_{fus}H_{molar,1}}{R} \left( \dfrac{T_m- T_m^*}{T_m^* T_m} \right) ≈ \dfrac{Δ_{fus}H_{molar,1}}{R} \left(\dfrac{ -ΔT}{T_m^{*2}} \right) \nonumber \]
This is often rewritten in terms of molality as:
\[ΔT = K_f.m \nonumber \]
If Kf is known for the solvent we can add a number of grams of an unknown compound to the solvent measure the temperature depression, this tells us the molality. From molality and weight we can then calculate molar mass. Boiling point elevation is quite similar.

