13.6: Electronic Spectra Contain Electronic, Vibrational, and Rotational Information
- Page ID
- 2399
Molecules can also undergo changes in electronic transitions during microwave and infrared absorptions. The energy level differences are usually high enough that it falls into the visible to UV range; in fact, most emissions in this range can be attributed to electronic transitions.
Electron Transitions are not Purely Electronic
We have thus far studied rovibrational transitions--that is, transitions involving both the vibrational and rotational states. Similarly, electronic transitions tend to accompany both rotational and vibrational transitions. These are often portrayed as an electronic potential energy cure with the vibrational level drawn on each curve. Additionally, each vibrational level has a set of rotational levels associated with it.
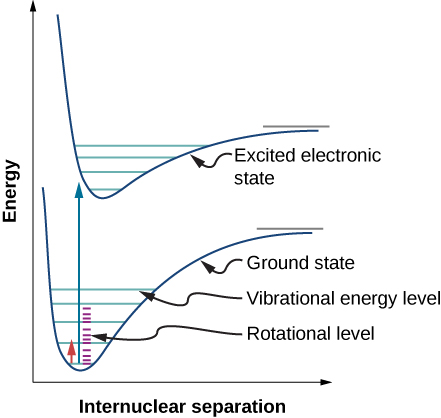
Recall that in the Born-Oppenheimer approximation, nuclear kinetic energies can be ignored (e.g., fixed) to solve for electronic wavefunctions and energies, which are much faster than rotation or vibration. As such, it is important to note that unlike rovibrational transitions, electronic transitions aren't dependent on rotational or transitional terms and are assumed to be separate. Therefore, when using an anharmonic oscillator-nonrigid rotator approximation (and excluding translation energy), the total energy of a diatomic is:
\[ \tilde{E}_{total} = \tilde{\nu}_{el} + G(v) + F(J) \label{Eqa1} \]
where \( \tilde{\nu}_{el}\) is the electronic transition energy change in wavenumbers, \(G(n)\) is the vibrational energy with energy level \(v\) (assuming anharmonic oscillator), and \(F(J)\) is the rotational energy, assuming a nonrigid rotor. Equation \(\ref{Eqa1}\) can be expanded accordingly:
\[ \tilde{E}_{total} = \underbrace{\tilde{\nu}_{el}}_{\text{electronic}} + \underbrace{\tilde{\nu}_e \left (v + \dfrac{1}{2} \right) - \tilde{\chi}_e \tilde{\nu}_e \left (v + \dfrac{1}{2} \right)^2}_{\text{vibrational}} + \underbrace{\tilde{B} J(J + 1) - \tilde{D} J^2(J + 1)^2}_{\text{rotational}} \label{Eqa2} \]
Notice that both the vibration constant (\( \tilde{\nu}_e\)) and anharmonic constant ( \(\tilde{\chi}_e\)) are electronic state dependent (and hence the rotational constants would be too, but are ignored here). Since rotational energies tend to be so small compared to electronic, their effects are minimal and are typically ignored when we do calculations and are referred to as vibronic transitions.

The eigenstate-to-eigenstate transitions (e.g., \(1 \rightarrow 2\)) possible are numerous and have absorption lines at
\[ \tilde{\nu}_{obs} = \tilde{E}_{2} - \tilde{E}_{1} \label{Eqa21} \]
and for simplification, we refer to constants associated with these states as \(| ' \rangle \) and \(| '' \rangle \), respectively. So Equation \(\ref{Eqa21}\) is
\[ \tilde{\nu}_{obs} = \tilde{E''(v'')} - \tilde{E'(v')} \nonumber \]
Also important to note that typically vibronic transitions are usually the result of the vibrational \(v'=0\) vibratonal state. Within this assumption and excluding the rotational contributions (due to their low energies), Equation \(\ref{Eqa2}\) can be used with Equation \(\ref{Eqa21}\) to get
\[ \tilde{\nu}_{obs} = \tilde{T}_{el} + \left( \dfrac{1}{2} \tilde{\nu}'_e - \dfrac{1}{4} \tilde{\chi}'_e \tilde{\nu}_e' \right) - \left( \dfrac{1}{2} \tilde{\nu}''_e - \dfrac{1}{4} \tilde{\chi}''_e \tilde{\nu}_e'' \right) + \tilde{\nu}'_e v'' - \tilde{\chi}'_e \tilde{\nu}_e' v''(v''+1) \label{Eqa3} \]
A common transition of importance is the \( \tilde{\nu}_{00}\), which is the \(0 \rightarrow 0\) transition and include no vibrational change. For this case, equation \(\ref{Eqa3}\) is then
\[ \tilde{\nu}_{00} = \tilde{T}_{el} + \left( \dfrac{1}{2} \tilde{\nu}'_e - \dfrac{1}{4} \tilde{\chi}'_e \tilde{\nu}_e' \right) - \left( \dfrac{1}{2} \tilde{\nu}''_e - \dfrac{1}{4} \tilde{\chi}''_e \tilde{\nu}_e'' \right) \nonumber \]
This is the lowest energy possible to observe in an electronic transition although it may be of low intensity as discussed in the following section.
The absorption spectrum of iodine yields information about the excited state well rather than the ground state well (notice that equation \(\ref{Eqa3}\) depends primarily on excited state parameters). In this experiment you will characterize the excited state well by extracting values for the following excited state parameters.
Recall that as \(v'\) increases, the vibrational energy spacing decreases. At the upper edge of the well, the vibrational energy spacing decreases to 0, which means that the energies form a continuum rather than being quantized. It is at this limit that bond dissociation occurs. The energy required to dissociate the bond is actually \(D_o'\) rather than \(D_e'\) because the molecule cannot have less than the zero point energy.
The vibrational-electronic spectrum of I2 in the region from 500-650 nm displays a large number of well-defined bands which, for the most part, correspond to v'<-- 0 transitions connecting the v" = 0 vibrational level of the ground electronic state (denoted as X1Σ+) to many different vibrational levels v' of the excited B3Π electronic state. Under the conditions of this experiment (i.e., low resolution), the rotational lines within each band are not resolved. However, the peaks may be identified as R-branch band heads (1). For a molecule as heavy as I2, the position of each band head is within a few tenths of one cm-1 of the band origin (2), and for the purposes of this experiment, the distinction between the two may be ignored. The general features of the absorption spectrum are shown below:
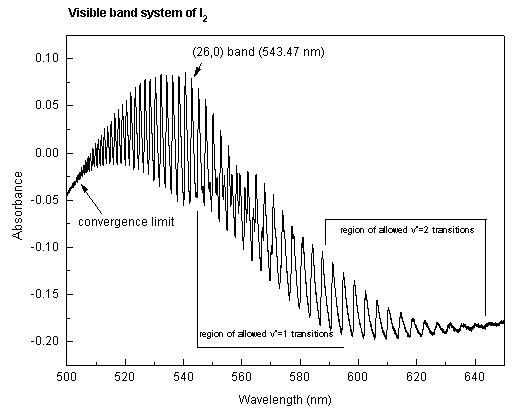
Each small bump, or peak, such as the (26,0) band labelled on the spectrum, corresponds to a transition between two vibrational levels and is called a band. Each band is comprised of several hundred lines, each of which involves different upper and lower rotational quantum numbers; as mentioned, these lines are not resolved in the present experiment. The region of maximum absorption in each band is caused by many of these lines falling together; it is called the band head. The set of all of these bands is referred to as the visible band system of I2.
If the sample is hot, then excited vibrational levels of the ground state may be populated, and these also will absorb light. The hot bands arising from absorption from v"=1 and v"=2 are shown very approximately on the absorption spectrum above.
At a point called the convergence limit, the spacing between bands decreases to zero. Beyond this convergence limit, the spectrum is continuous because the excited state of the I2 molecule is not bound. One of the purposes of this experiment is to identify this convergence limit accurately.

