13.7: The Franck-Condon Principle
- Page ID
- 13670
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- To explain the vibrational fine structure in electronic spectroscopy for bound excited states in terms of the Franck‐Condon approximation
- To calculate the vibrational progressions (Franck-Condon factors) in a single displaced harmonic oscillator vibronic system.
The Franck-Condon Principle describes the intensities of vibronic transitions, or the absorption or emission of a photon. It states that when a molecule is undergoing an electronic transition, such as ionization, the nuclear configuration of the molecule experiences no significant change. This is due in fact that nuclei are much more massive than electrons and the electronic transition takes place faster than the nuclei can respond. When the nucleus realigns itself with the new electronic configuration, the theory states that it must undergo a vibration.
If we picture the vertical transition from ground to excited electronic state as occurring from a vibrational wavefunction that gives a probability distribution of finding the nuclei in a give region of space we can determine the probability of a given vibrational level from the overlap integral \(S_{v’,v}\) which gives the overlap of the vibrational wavefunction in the ground and excited state. The \(v’\) quantum numbers refer to the ground state and the \(v\) quantum numbers refer to the excited state. The transition probability can be separated into electronic and nuclear parts using the Condon approximation.
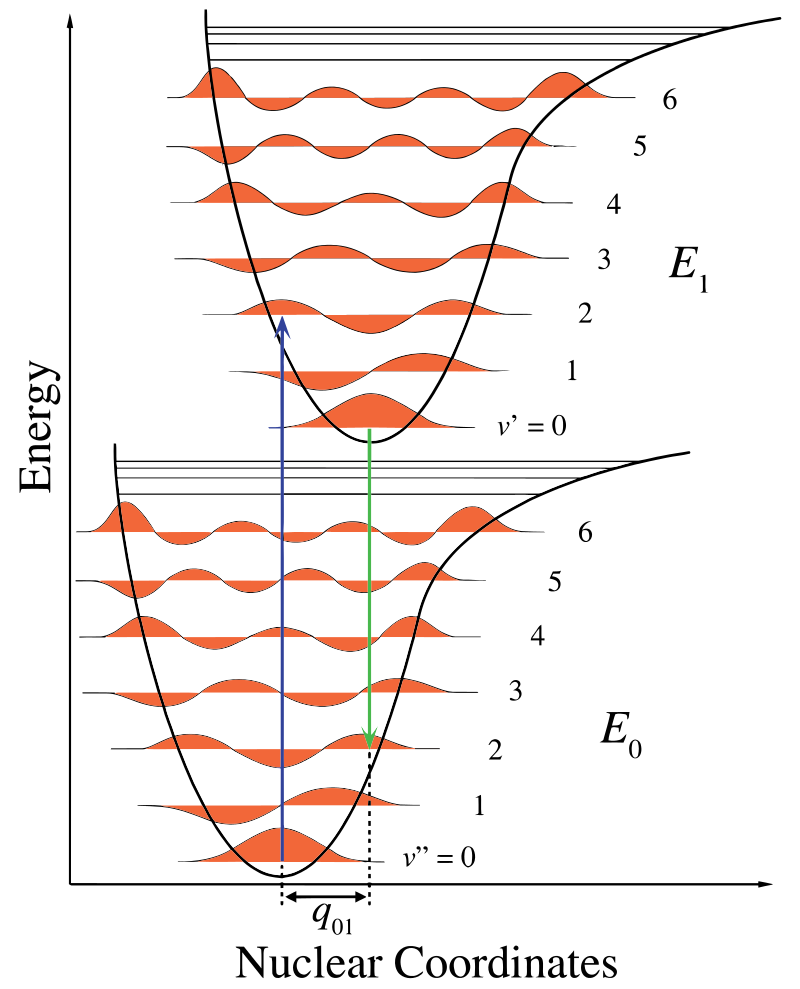
In Figure 13.7.1 , the nuclear axis shows a consequence of the internuclear separation and the vibronic transition is indicated by the blue and green vertical arrows. This figure demonstrates three things:
- An absorption leads to a higher energy state,
- fluorescence leads to a lower energy state, and
- the shift in nuclear coordinates between the ground and excited state is indicative of a new equilibrium position for nuclear interaction potential. The fact that the fluorescence arrow is shorter than the absorption indicates that it has less energy, or that its wavelength is longer.
Condon approximation is the assumption that the electronic transition occurs on a time scale short compared to nuclear motion so that the transition probability can be calculated at a fixed nuclear position.
This change in vibration is maintained during a state termed the rapid electronic excitation. The resulting Coulombic forces produce an equilibrium as shown in the figure for the nuclei termed a turning point. The turning point can be mapped by drawing a vertical line from the minimum of the lower curve to the intersection of the higher electronic state. This procedure is termed a vertical transition and was discussed before in the context of photoelectron spectroscopy (another electronic spectroscoy).
The Franck-Condon Principle explains the relative intensities of vibronic transitions by relating the probability of a vibrational transition to the overlap of the vibrational wavefunctions. It states that the probability of a vibrational transition occurring is weighted by the Franck-Condon overlap integral:
\[P_{i \rightarrow f} = | \langle \psi^*_{final} | \boldsymbol{\mu} | \psi_{initial} \rangle | ^2 = | \int \psi^*_{final} \boldsymbol{\mu} \psi_{initial} d\tau | ^2 \nonumber \]
Within the Franck-Condon approximation, the nuclei are considered "fixed" during electronic transitions. Thus, electronic transitions can be considered vertical transitions on electronic potential energy curves (vierical transitions in Figure 13.7.1 ).
The Franck-Condon Principle has both a Classical and Quantum application. Classically, the Franck–Condon principle is the approximation that an electronic transition is most likely to occur without changes in the positions of the nuclei in the molecular entity and its environment. The resulting state is called a Franck–Condon state, and the transition involved, a vertical transition. The quantum mechanical formulation of this principle is that the intensity of a vibronic transition is proportional to the square of the overlap integral between the vibrational wavefunctions of the two states that are involved in the transition.
The Franck-Condon principle is based on the Born-Oppenheimer approximation, which allows separation of the electronic \(q\) and nuclear \(Q\) wavefunctions given the total wavefunction.
\[ | \psi_{total}(Q,q) = | \psi_{nuc}(Q) \rangle \psi_{el} (Q;q) \rangle \nonumber \]
Since the transition operator, \(\hat{\mu}(q)\), is dependent only on the electronic component, the nuclear components can be separated from the transition moment integral that dictates the probability of the transition occurring:
\[ \begin{align} \langle \psi^{*}_{total, f} | \hat{\mu} | \psi_{total, i} \rangle &= \langle \psi^*_{nuc, f} | \langle \psi^{*}_{el, f} | {\boldsymbol{\mu}} | \psi_{el, i} \rangle | \psi_{nuc, i} \rangle \\[4pt] &= \underbrace{ \langle \psi^{*}_{nuc, f} | \psi_{nuc, i} \rangle}_{\text{nuclear overlap}} \langle \psi^{*}_{el, f} | {\boldsymbol{\mu}} | \psi_{el, i} \rangle \end{align} \nonumber \]
If the nuclear overlap integral is zero for this transition, then the transition will not be observed, irrespective of the magnitude of the electronic factor.
\(S_{00}\) Transition Evaluated within Harmonic Oscillator Model
The nuclear overlap for the zero-zero transition \(S_{00}\) can be calculated quite simply using the definition of the Gaussian form of the harmonic oscillator wavefunctions.
The zero-point wavefunction in the ground electronic state is
\[ | \psi(R) \rangle = \big| \left(\dfrac{\alpha}{\pi} \right)^{1/4} e ^{-\alpha(R-R_e)^2/2} \big\rangle \nonumber \]
The zero-point wavefunction in the excited electronic state is
\[ | \psi(R) \rangle = \big | \left(\dfrac{\alpha}{\pi} \right)^{1/4} e ^{-\alpha(R-Q_e)^2/2} \big\rangle \nonumber \]
where
- \(\alpha = \dfrac{\sqrt{mk}}{\hbar}\)
- \(R_e\) is the equilibrium bond length in the ground electronic state
- \(Q_e\) is the equilibrium bond length in the excited electronic state
The nuclear overlap integral is
\[ S_{00}= \langle \psi^*_{nuc, f} | \psi_{nuc, i} \rangle = \sqrt{\dfrac{\alpha}{\pi}} \int_{\infty}^{\infty} e ^{-\alpha(R-R_e)^2/2} e ^{-\alpha(R-Q_e)^2/2} dR \label{FC1} \]
The exponent in Equation \(\ref{FC1}\) can be expanded as
\[ S_{00}= \sqrt{\dfrac{\alpha}{\pi}} \int_{\infty}^{\infty} e ^{-\alpha(2R^2-RR_e - 2RQ_e+ R^2_e + Q_e^2)/2} dR \label{FC2} \]
and we use
\[(R_e + Q_e)^2 = R_e^2 + Q_e^2 + 2R_eQ_e \nonumber \]
and
\[(R_e - Q_e)^2 = R_e^2 + Q_e^2 - 2R_eQ_e \nonumber \]
to substitute and complete the square inside the integral. We can express
\[R_e^2 + Q_e^2 = \dfrac{1}{2}[(R_e + Q_e)^2 + (R_e - Q_e)^2]. \nonumber \]
Thus, the integral in Equation \(\ref{FC2}\) is
\[S_{00}= \sqrt{\dfrac{\alpha}{\pi}} e^{-\alpha(R_e -Q_e)^2/4} \int_{-\infty}^{\infty} e ^{-\alpha\{R- 1/2(R_e+Q_e)\}^2} dR \nonumber \]
The integral is a Gaussian integral. You can show that if we let \(z = \sqrt{\alpha}\{R-1/2(R_e + Q_e)\}\) then \(dz = \sqrt{\alpha} dR\) and the integral becomes
\[S_{00}= \sqrt{\dfrac{\alpha}{\pi}} e^{-\alpha(R_e -Q_e)^2/4} \dfrac{1}{\sqrt{\alpha}} \int_{-\infty}^{\infty} e^{z^2} dz \label{FC3} \]
this integral has been solved already, from a table of integrals, Equation \(\ref{FC3}\) becomes
\[ S_{00} = e^{-\alpha(R_e-Q_e)^2/4} \nonumber \]
We would follow the same procedure to calculate that overlap of the zeroth level vibration in the ground to the first excited vibrational level of the excited state: \(S_{01}\).
\(S_{01}\) Transition Evaluated within Harmonic Oscillator Model
To calculate the overlap of zeroth ground state level (\(v=0\)) with the first excited state level (\(v'=1\)) we use the Hermite polynomial \(H_1(x) =2x\) for describing the excited state wavefunction (see here for a review on harmonic oscillator wavefunctions). Here \(x = \sqrt{\alpha}(R - Q_e)\).
\[ S_{01}= \langle \psi^{*}_{nuc, f} | \psi_{nuc, i} \rangle \label{FC01} \]
with the zero-point wavefunction in the ground electronic state is
\[ | \psi(R) \rangle = \big| \left(\dfrac{\alpha}{\pi} \right)^{1/4} e ^{-\alpha(R-R_e)^2/2} \big\rangle \nonumber \]
The first excited-state wavefunction in the excited electronic state is
\[ | \psi(R) \rangle = \big | \left(\dfrac{\alpha}{\pi} \right)^{1/4} \sqrt{\alpha}2 (R-Q_e) e^{-\alpha(R-Q_e)^2/2} \big\rangle \nonumber \]
The overlap of zeroth ground state level with the first excited state level (Equation \(\ref{FC01}\)) is then
\[ S_{01} = \dfrac{1}{\sqrt{2}} \sqrt{\dfrac{\alpha}{\pi}} \int_{-\infty}^{\infty} e^{-\alpha(R-R_e)^2/2} \sqrt{\alpha}2 (R-Q_e) e^{-\alpha(R-Q_e)^2/2} \nonumber \]
and
\[ S_{01} = \sqrt{\dfrac{2 \alpha^2}{\pi}} e^{-\alpha(R_e-Q_e)^2/4} \int_{-\infty}^{\infty} (R-Q_e) e^{-\alpha \{R- 1/2 (R_e+Q_e)^2\}} \nonumber \]
The same substitutions can be made as above so that the integral can be written as (not shown and to be demonstrated in a homework exercises) and the final result is
\[S_{01} = \sqrt{\dfrac{\alpha^2}{2}} (R_e-Q_e) e^{-\alpha(R_e-Q_e)^2/4} \nonumber \]
We could continue and calculate that overlap of the zeroth level in the ground state with all the higher light vibrational levels: \(S_{02}\), \(S_{03}\), etc. Each term corresponds to a transition with a different energy since the vibrational levels have different energies. The absorption band then has the appearance of a progression (a Franck-Condon progression) of transitions between different levels each with its own probability.
Franck-Condon Progressions
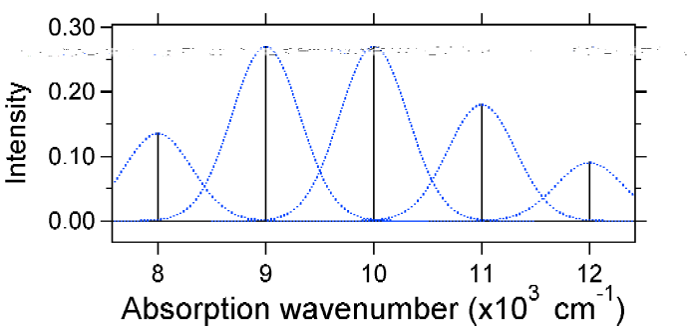
To understand the significance of the above formula for the FC factor, let us examine a ground and excited state potential energy surface at \(T = 0\) Kelvin. Shown below are two states separated by 8,000 cm-1 in energy. This is energy separation between the bottoms of their potential wells, but also between the respective zero-point energy levels. Let us assume that the wavenumber of the vibrational mode is 1,000 cm-1 and that the bond length is increased due to the fact that an electron is removed from a bonding orbital and placed in an anti-bonding orbital upon electronic excitation.
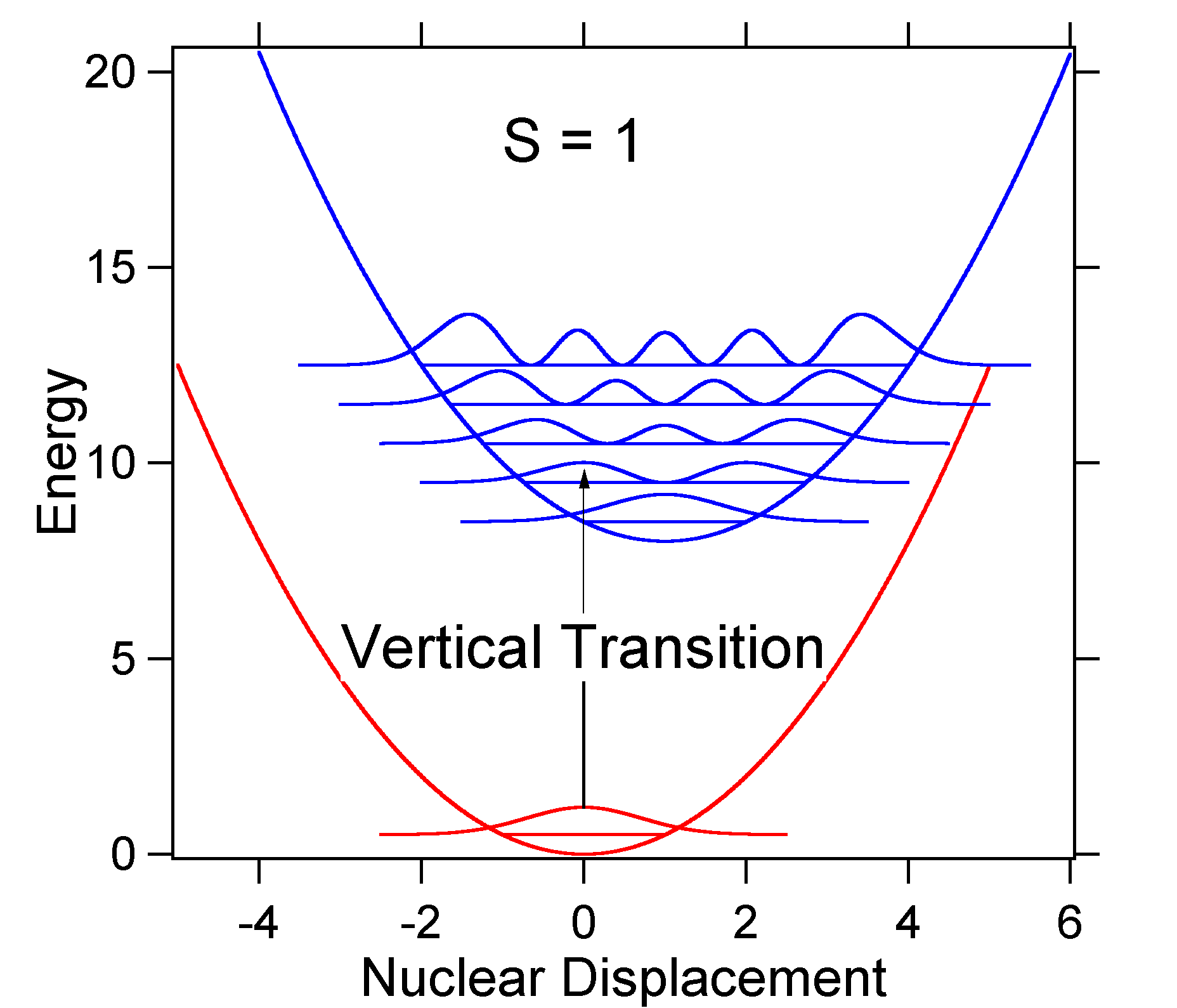
According to the above model for the Franck-Condon factor we would generate a "stick" spectrum (Figure 13.7.3 ) where each vibrational transition is infinitely narrow and transition can only occur when \(E = h\nu\) exactly. For example, the potential energy surfaces were given for S = 1 and the transition probability at each level is given by the sticks (black) in the figure below.
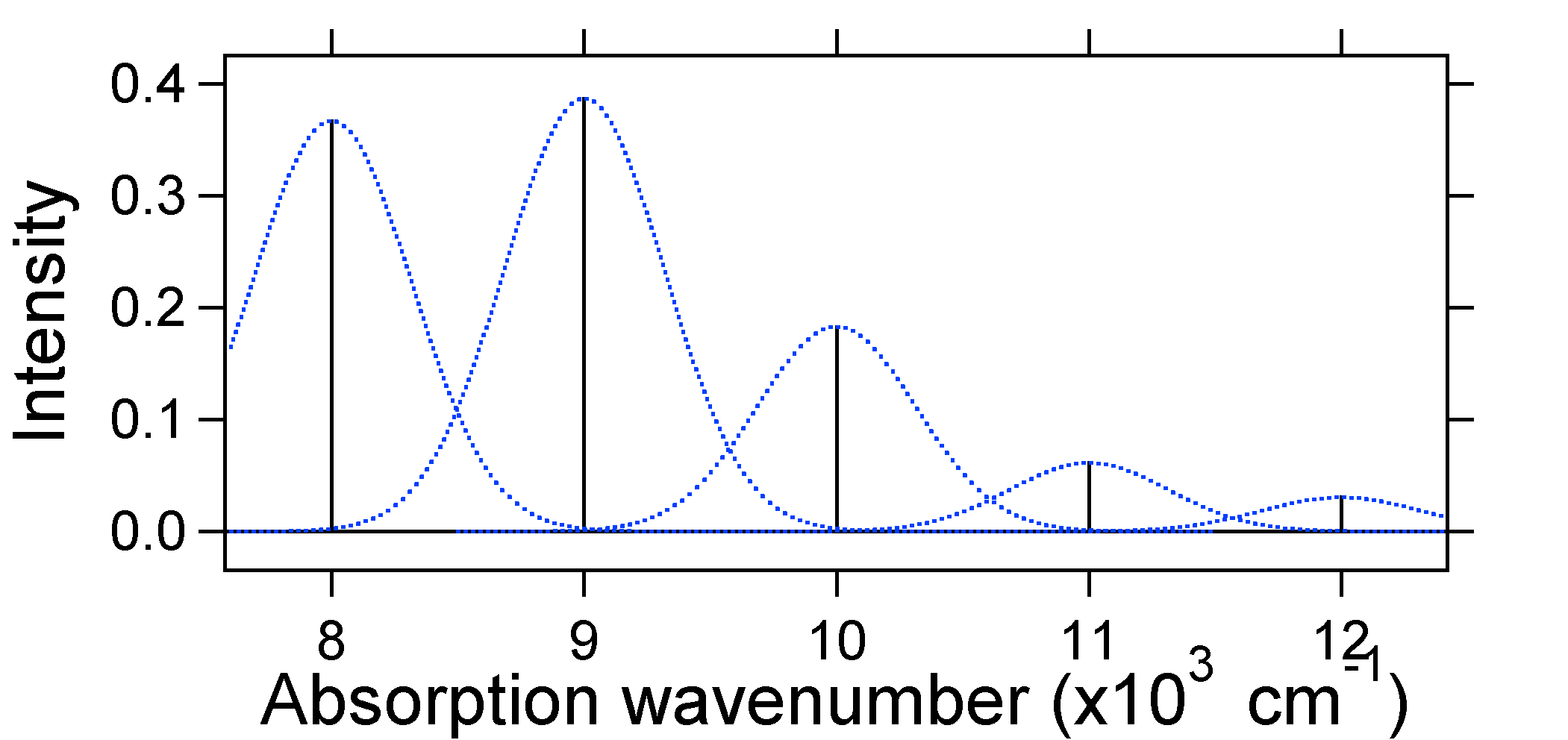
The dotted Gaussians that surround each stick give a more realistic picture of what the absorption spectrum should look like. In this first place each energy level (stick) will be given some width by the fact that the state has a finite lifetime. Such broadening is called homogeneous broadening since it affects all of the molecules in the ensemble in a similar fashion. There is also broadening due to small differences in the environment of each molecule. This type of broadening is called inhomogeneous broadening. Regardless of origin the model above was created using a Gaussian broadening
The nuclear displacement between the ground and excited state determines the shape of the absorption spectrum. Let us examine both a smaller and a large excited state displacement. If \(S = ½\) and the potential energy surfaces in this case are:
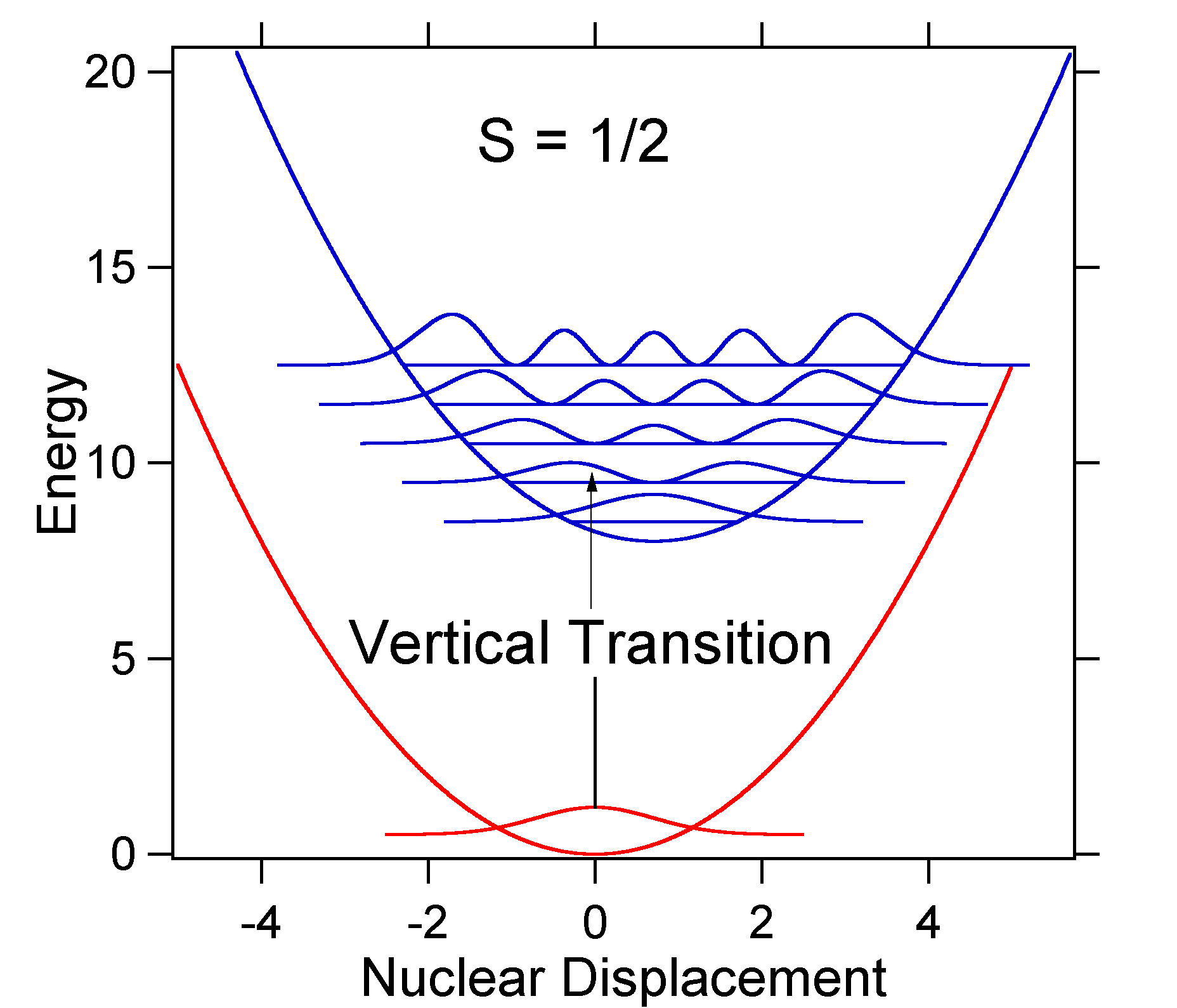
For this case the "stick" spectrum has the appearance in Figure 13.7.5
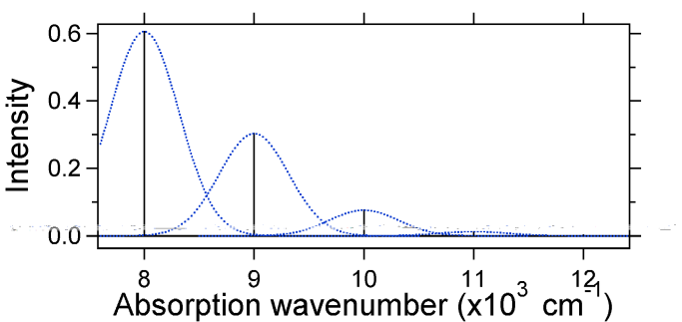
Note that the zero-zero or \(S_{0,0}\) vibrational transition is much large in the case where the displacement is small.
As a general rule of thumb the \(S\) constant gives the ratio of the intensity of the \(v = 2\) transition to the \(v = 1\) transition. In this case since \(S = 0.5\), the \(v=2\) transition is 0.5 the intensity of \(v=1\) transition.
As an example of a larger displacement the disposition of the potential energy surfaces for S = 2 is shown below.
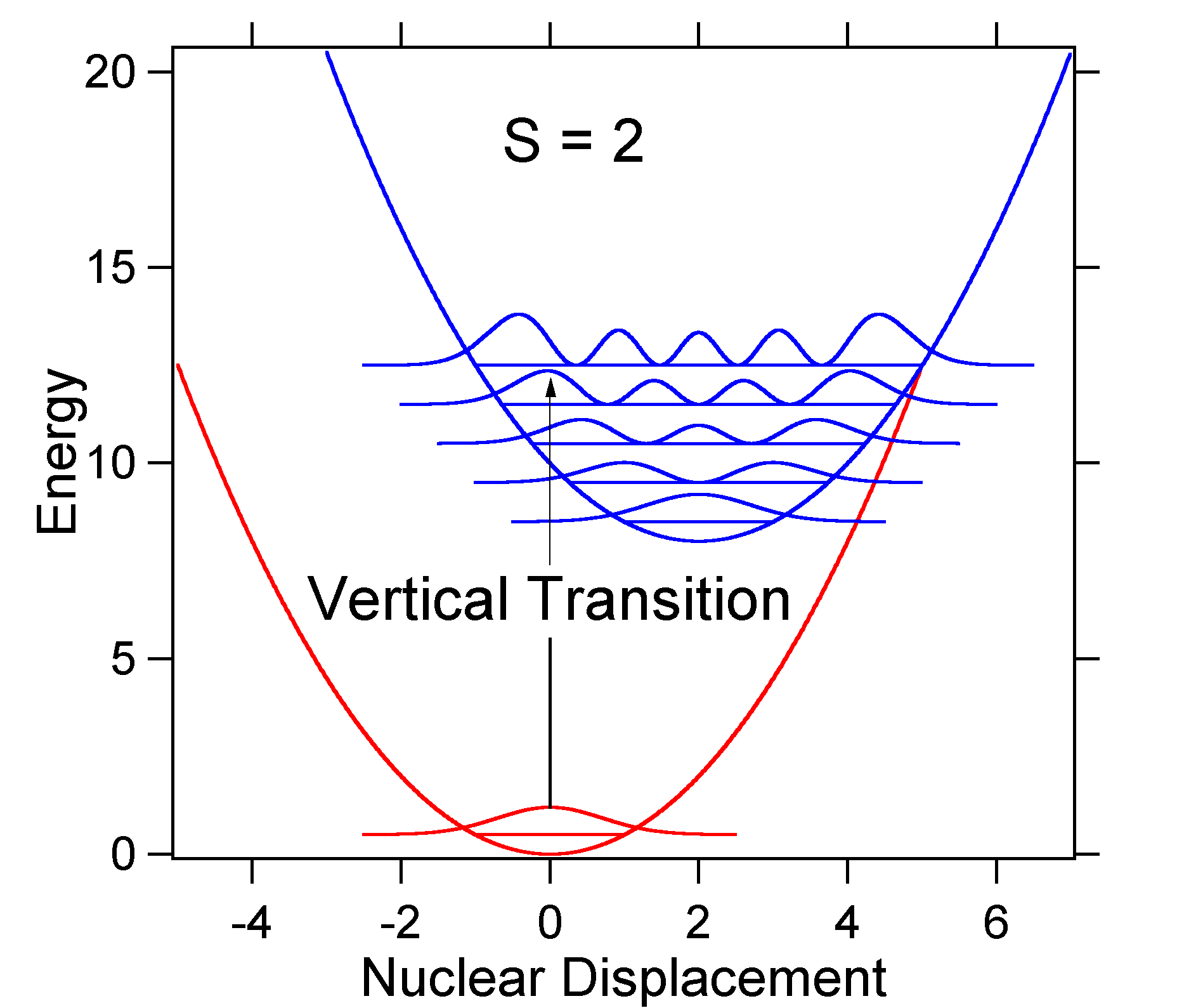
The larger displacement results in decreased overlap of the ground state level with the v = 0 level of the excited state. The maximum intensity will be achieved in higher vibrational levels as shown in the stick spectrum.
The absorption spectra plotted below all have the same integrated intensity, however their shapes are altered because of the differing extent of displacement of the excited state potential energy surface.
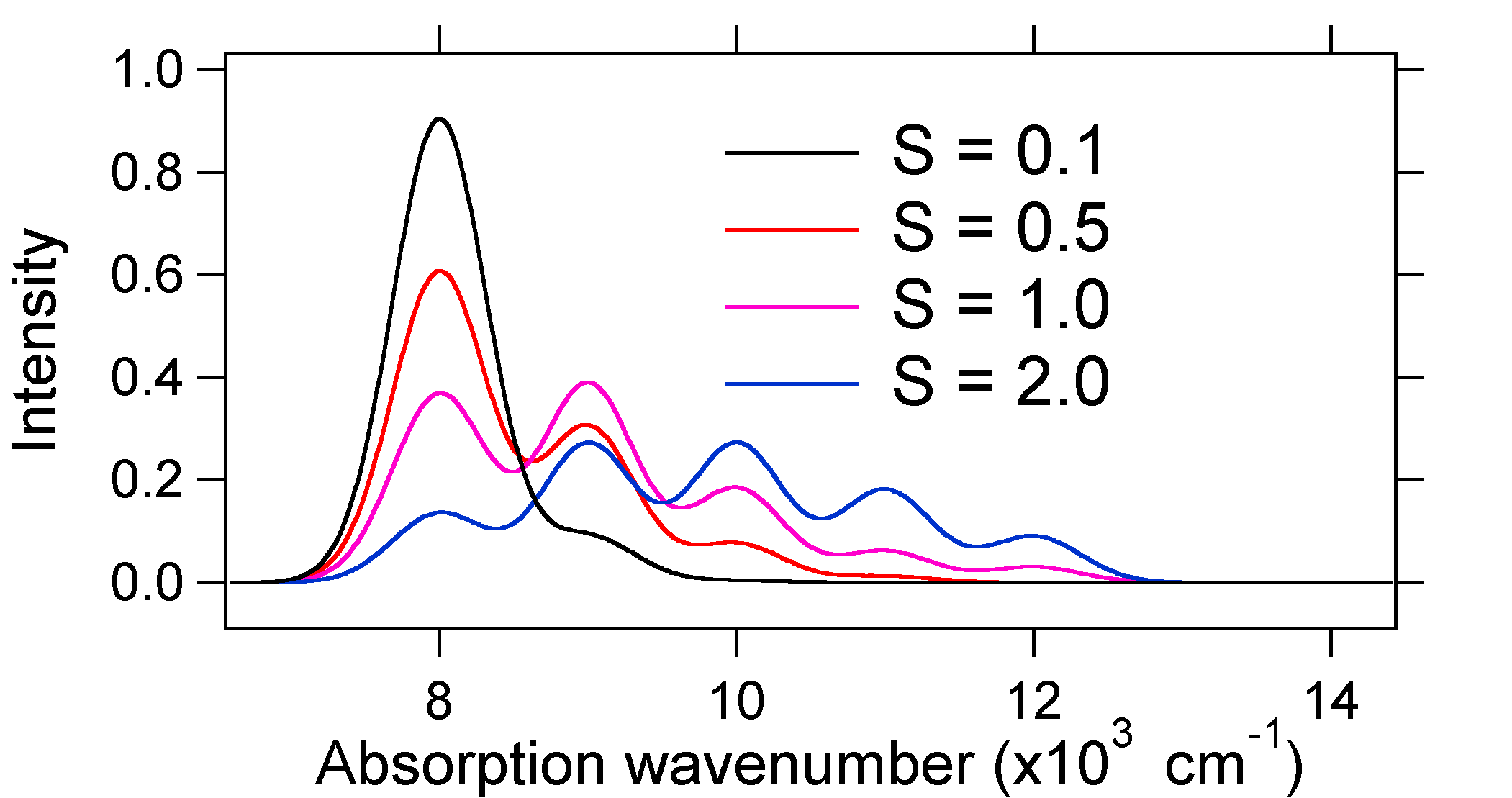
So the nature of the relative vibronic band intensities can tell us whether there is a displacement of the equilibrium nuclear coordinate that accompanied a transition. When will there be an increase in bond length (i.e., \(Q_e > R_e\))? This occurs when an electron is promoted from a bonding molecular orbital to a non-bonding or anti-bonding molecular orbitals (i.e., when the bond order is less in the excited state than the ground state).
- Non-bonding molecular orbital \(\rightarrow\) bonding molecular orbital
- Anti-bonding molecular orbital \(\rightarrow\) bonding molecular orbital
- Anti-bonding molecular orbital \(\rightarrow\) non-bonding molecular orbital
In short, when the bond order is lower in the excited state than in the ground state, then \(Q_e > R_e\); an increase in bond length will occur when this happens.
References
- Atkins, Peter and Julio de Paula. Physical Chemistry for the Life Sciences. 2006. New York, NY: W.H. Freeman and Company. p. 563-564
- Franck-Condon Principle. 1996, 68, 2243. IUPAC Compendium of Chemical Terminology 2nd Edition (1997). www.iupac.org/goldbook/F02510.pdf
- E.Rabinowitch and Govindjee. Light Absorption and Fate of Excitation of Energy. 1969. Franck-Condon Principle. http://www.life.uiuc.edu/govindjee/b...em494/Abs.html

