20.7G: Help on using Tanabe-Sugano diagrams
- Page ID
- 97482
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
To make use of the Tanabe-Sugano diagrams provided in textbooks, it would be expected that they should at least be able to cope with typical spectra for d3, d8 octahedral and d2, d7 tetrahedral systems since these are predicted to be the most favoured from Crystal Field Stabilisation calculations. This is not the case. All the diagrams presented are impractical, being far too small and for chromium(III) actually stop before the region of interest of many simple coordination complexes.
If we ignore spin-forbidden transitions, where the energy of the states depend on both the B and C Racah parameter, then it should be possible to use the dn, d10-n relationship between octahedral and tetrahedral for interpretation of the spin-allowed transitions. This is because, for example, the d3 octahedral and d7 tetrahedral states have the same energy dependencies on Δ/B. When using the Tanabe-Sugano diagram in this way the major difference is that the size of Δ tetrahedral is only roughly 4/9 times that of Δ octahedral and so all complexes are high spin and the area of interest is moved closer to the left hand side of the diagram.
- Record the UV/Vis spectrum of your sample.
- Tabulate peak information in wavelengths (nm) and convert to wavenumbers (cm-1), {ν = 107 / λ}
- calculate the extinction coefficients based on the concentration
- calculate the experimental ratio of v2 / v1
- use the appropriate Tanabe-Sugano diagram to locate where the ratio of the second to first peak matches that of the experimental value above.
The expected values should be compared to the following rough guide.
- For M2+ complexes, expect Δ= 7500 - 12500 cm-1.
- For M3+ complexes, expect Δ= 14000 - 25000 cm-1.
B for first-row transition metal free ions is around 1000 cm-1. Depending on the position of the ligand in the nephelauxetic series, this can be reduced to as low as 60% in the complex. Extinction coefficients for octahedral complexes are expected to be around 50-100 times smaller than for tetrahedral complexes. For a typical spin-allowed but Laporte (orbitally) forbidden transition in an octahedral complex, expect ε < 10 m2mol-1.
For an octahedral Ni(II) complex, three peaks were observed at 8000, 13200 and 22800 cm-1. From the ratio v2/v1 of 1.65 this gives a value of Δ/B' of 10.0. This can be shown in the following diagram.
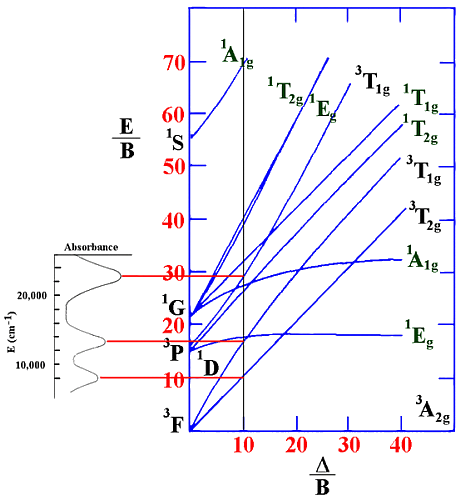
Since v1= Δ in this case (and equals 8000 cm-1) then B' can be evaluated to be 800 cm-1. The spin-forbidden lines that would be between v2 and v3 in energy are not observed in the spectrum nor are any lines seen at higher energy.
References
- Ligand Field Theory and its Applications, B.N. Figgis and M.A. Hitchman, Wiley-VCH, New York, 2000.
- Inorganic Chemistry, J.E. Huheey, 3rd Edition, Harper & Row Publishers, New York 1983.


For d2 (oct), d8 (tet) and d3, d8 (oct) d2, d7 (tet) JAVA applets and spreadsheets are available which perform these calculations.