11.3: Reaction Quotient
- Page ID
- 3531
Make sure you thoroughly understand the following essential ideas:
- When arbitrary quantities of the different components of a chemical reaction system are combined, the overall system composition will not likely correspond to the equilibrium composition. As a result, a net change in composition ("a shift to the right or left") will tend to take place until the equilibrium state is attained.
- The status of the reaction system in regard to its equilibrium state is characterized by the value of the equilibrium expression whose formulation is defined by the coefficients in the balanced reaction equation; it may be expressed in terms of concentrations, or in the case of gaseous components, as partial pressures.
- The various terms in the equilibrium expression can have any arbitrary value (including zero); the value of the equilibrium expression itself is called the reaction quotient Q.
- If the concentration or pressure terms in the equilibrium expression correspond to the equilibrium state of the system, then Q has the special value K, which we call the equilibrium constant.
- The ratio of Q/K (whether it is 1, >1 or <1) thus serves as an index of how far the system is from its equilibrium composition, and its value indicates the direction in which the net reaction must proceed in order to reach its equilibrium state.
- When Q = K, then the equilibrium state has been reached, and no further net change in composition will take place as long as the system remains undisturbed.
Consider a simple reaction such as the gas-phase synthesis of hydrogen iodide from its elements: \[H_2 + I_2 \rightarrow 2 HI\] Suppose you combine arbitrary quantities of \(H_2\), \(I_2\) and \(HI\). Will the reaction create more HI, or will some of the HI be consumed as the system moves toward its equilibrium state? The concept of the reaction quotient, which is the focus of this short lesson, makes it easy to predict what will happen.
What is the Equilibrium Quotient?
In the previous section we defined the equilibrium expression for the reaction
In the general case in which the concentrations can have any arbitrary values (including zero), this expression is called the reaction quotient (the term equilibrium quotient is also commonly used.) and its value is denoted by \(Q\) (or \(Q_c\) or \(Q_p\) if we wish to emphasize that the terms represent molar concentrations or partial pressures.) If the terms correspond to equilibrium concentrations, then the above expression is called the equilibrium constant and its value is denoted by \(K\) (or \(K_c\) or \(K_p\)).
\(K\) is thus the special value that \(Q\) has when the reaction is at equilibrium
The value of Q in relation to K serves as an index how the composition of the reaction system compares to that of the equilibrium state, and thus it indicates the direction in which any net reaction must proceed. For example, if we combine the two reactants A and B at concentrations of 1 mol L–1 each, the value of Q will be 0÷1=0. The only possible change is the conversion of some of these reactants into products. If instead our mixture consists only of the two products C and D, Q will be indeterminately large (1÷0) and the only possible change will be in the reverse direction.
For example, if we combine the two reactants A and B at concentrations of 1 mol L–1 each, the value of Q will be 0÷1=0. The only possible change is the conversion of some of these reactants into products. If instead our mixture consists only of the two products C and D, Q will be indeterminately large (1÷0) and the only possible change will be in the reverse direction.
It is easy to see (by simple application of the Le Chatelier principle) that the ratio of Q/K immediately tells us whether, and in which direction, a net reaction will occur as the system moves toward its equilibrium state. A schematic view of this relationship is shown below:
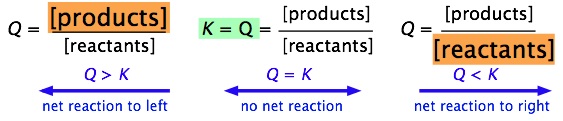
It is very important that you be able to work out these relations for yourself, not by memorizing them, but from the definitions of \(Q\) and \(K\).
| Condition | Status of System |
|---|---|
| Q > K | Product concentration too high for equilibrium; net reaction proceeds to left. |
| Q = K | System is at equilibrium; no net change will occur. |
| Q < K | Product concentration too low for equilibrium; net reaction proceeds to right. |
It is very important that you be able to work out these relations for yourself, not by memorizing them, but from the definitions of \(Q\) and \(K\).
The equilibrium constant for the oxidation of sulfur dioxide is Kp = 0.14 at 900 K.
\[\ce{2 SO_2(g) + O_2(g) \rightleftharpoons 2 SO_3(g)} \nonumber\]
If a reaction vessel is filled with SO3 at a partial pressure of 0.10 atm and with O2 and SO2 each at a partial pressure of 0.20 atm, what can you conclude about whether, and in which direction, any net change in composition will take place?
Solution:
The value of the equilibrium quotient Q for the initial conditions is
\[ Q= \dfrac{p_{SO_3}^2}{p_{O_2}p_{SO_2}^2} = \dfrac{(0.10\; atm)^2}{(0.20 \;atm) (0.20 \; atm)^2} = 1.25\; atm^{-1} \nonumber\]
Since Q > K, the reaction is not at equilibrium, so a net change will occur in a direction that decreases Q. This can only occur if some of the SO3 is converted back into products. In other words, the reaction will "shift to the left".
The formal definitions of Q and K are quite simple, but they are of limited usefulness unless you are able to relate them to real chemical situations. The following diagrams illustrate the relation between Q and K from various standpoints. Take some time to study each one carefully, making sure that you are able to relate the description to the illustration.
For the reaction
\[N_2O_{4(g)} \rightleftharpoons 2 NO_{2(g)} \nonumber\]
Kc = 0.0059 at 298 K.
This equilibrium condition is represented by the red curve that passes through all points on the graph that satisfy the requirement that
\[Q = \dfrac{[NO_2]^2}{ [N_2O_4]} = 0.0059 \nonumber\]
There are of course an infinite number of possible Q's of this system within the concentration boundaries shown on the plot. Only those points that fall on the red line correspond to equilibrium states of this system (those for which \(Q = K_c\)). The line itself is a plot of [NO2] that we obtain by rearranging the equilibrium expression
\[[NO_2] = \sqrt{[N_2O_4]K_c} \nonumber\]
If the system is initially in a non-equilibrium state, its composition will tend to change in a direction that moves it to one that is on the line. Two such non-equilibrium states are shown. The state indicated by  has \(Q > K\), so we would expect a net reaction that reduces Q by converting some of the NO2 into N2O4; in other words, the equilibrium "shifts to the left". Similarly, in state
has \(Q > K\), so we would expect a net reaction that reduces Q by converting some of the NO2 into N2O4; in other words, the equilibrium "shifts to the left". Similarly, in state  , Q < K, indicating that the forward reaction will occur.
, Q < K, indicating that the forward reaction will occur.
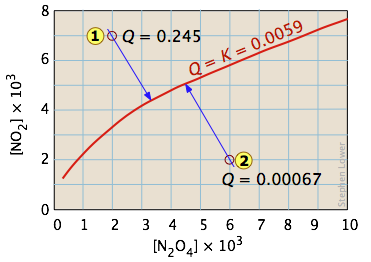
The blue arrows in the above diagram indicate the successive values that Q assumes as the reaction moves closer to equilibrium. The slope of the line reflects the stoichiometry of the equation. In this case, one mole of reactant yields two moles of products, so the slopes have an absolute value of 2:1.
One of the simplest equilibria we can write is that between a solid and its vapor. In this case, the equilibrium constant is just the vapor pressure of the solid. Thus for the process
\[I_{2(s)} \rightleftharpoons I_{2(g)} \nonumber\]
all possible equilibrium states of the system lie on the horizontal red line and is independent of the quantity of solid present (as long as there is at least enough to supply the relative tiny quantity of vapor.)
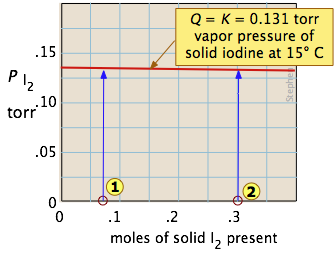
So adding various amounts of the solid to an empty closed vessel (states  and
and  ) causes a gradual buildup of iodine vapor. Because the equilibrium pressure of the vapor is so small, the amount of solid consumed in the process is negligible, so the arrows go straight up and all lead to the same equilibrium vapor pressure.
) causes a gradual buildup of iodine vapor. Because the equilibrium pressure of the vapor is so small, the amount of solid consumed in the process is negligible, so the arrows go straight up and all lead to the same equilibrium vapor pressure.
The decomposition of ammonium chloride is a common example of a heterogeneous (two-phase) equilibrium. Solid ammonium chloride has a substantial vapor pressure even at room temperature:
\[NH_4Cl_{(s)} \rightleftharpoons NH_{3(g)} + HCl_{(g)}\]
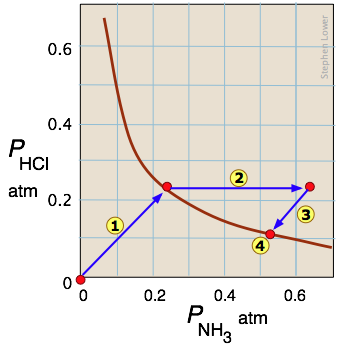
Arrow  traces the states the system passes through when solid NH4Cl is placed in a closed container. Arrow
traces the states the system passes through when solid NH4Cl is placed in a closed container. Arrow  represents the addition of ammonia to the equilibrium mixture; the system responds by following the path
represents the addition of ammonia to the equilibrium mixture; the system responds by following the path  back to a new equilibrium state
back to a new equilibrium state which, as the Le Chatelier principle predicts, contains a smaller quantity of ammonia than was added. The unit slopes of the paths
which, as the Le Chatelier principle predicts, contains a smaller quantity of ammonia than was added. The unit slopes of the paths  and
and  reflect the 1:1 stoichiometry of the gaseous products of the reaction.
reflect the 1:1 stoichiometry of the gaseous products of the reaction.


