Tetrahedral vs. Square Planar Complexes

Learning Objectives

• Discuss the d-orbital degeneracy of square planar and tetrahedral metal complexes.

Tetrahedral Geometry

Tetrahedral geometry is a bit harder to visualize than square planar geometry. Tetrahedral geometry is analogous to a pyramid, where each of corners of the pyramid corresponds to a ligand, and the central molecule is in the middle of the pyramid. This geometry also has a coordination number of 4 because it has 4 ligands bound to it. Finally, the bond angle between the ligands is 109.5^o. An example of the tetrahedral molecule \(\ce{CH4}\), or methane.

In a tetrahedral complex, \(Δ_t\) is relatively small even with strong-field ligands as there are fewer ligands to bond with. It is rare for the \(Δ_t\) of tetrahedral complexes to exceed the pairing energy. Usually, electrons will move up to the higher energy orbitals rather than pair. Because of this, most tetrahedral complexes are high spin.

Square Planar Complexes

In square planar molecular geometry, a central atom is surrounded by constituent atoms, which form the corners of a square on the same plane. The geometry is prevalent for transition metal complexes with d⁸ configuration. This includes Rh(I), Ir(I), Pd(II), Pt(II), and Au(III). Notable examples include the anticancer drugs cisplatin (\(\ce{PtCl2(NH3)2}\)).

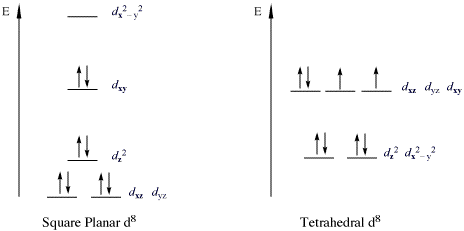
A square planar complex also has a coordination number of 4. The structure of the complex differs from tetrahedral because the ligands form a simple square on the x and y axes. Because of this, the crystal field splitting is also different (Figure \(\PageIndex{1}\)). Since there are no ligands along the z-axis in a square planar complex, the repulsion of electrons in the \(d_{xz}\), \(d_{yz}\), and the \(d_{z^2}\) orbitals are considerably lower than that of the octahedral complex (the \(d_{z^2}\) orbital is slightly higher in energy to the "doughnut" that lies on the x,y axis). The \(d_{x^2-y^2}\) orbital has the most energy, followed by the \(d_{xy}\) orbital, which is followed by the remaining orbtails (although \(d_{z^2}\) has slightly more energy than the \(d_{xz}\) and \(d_{yz}\) orbital). This pattern of orbital splitting remains constant throughout all geometries. Whichever orbitals come in direct contact with the ligand fields will have higher energies than orbitals that slide past the ligand field and have more of indirect contact with the ligand fields. So when confused about which geometry leads to which splitting, think about the way the ligand fields interact with the electron orbitals of the central atom.

Figure \(\PageIndex{1}\): In square planar complexes Δ will almost always be large, even with a weak-field ligand. Electrons tend to be paired rather than unpaired because paring energy is usually much less than Δ. Therefore, square planar complexes are usually low spin. (CC BY-SA; Ümit Kaya)

In square planar complexes \(Δ\) will almost always be large (Figure \(\PageIndex{1}\)), even with a weak-field ligand. Electrons tend to be paired rather than unpaired because paring energy is usually much less than \(Δ\). Therefore, square planar complexes are usually low spin.

Advanced: \(\ce{[PdCl4]^{2-}}\) is square planar and \(\ce{[NiCl4]^{2-}}\) is tetrahedral

The molecule \(\ce{[PdCl4]^{2−}}\) is diamagnetic, which indicates a square planar geometry as all eight d-electrons are paired in the lower-energy orbitals. However, \(\ce{[NiCl4]^{2−}}\) is also d⁸ but has two unpaired electrons, indicating a tetrahedral geometry. Why is \(\ce{[PdCl4]^{2−}}\) square planar if \(\ce{Cl^{-}}\) is not a strong-field ligand?

Solution

The geometry of the complex changes going from \(\ce{[NiCl4]^{2−}}\) to \(\ce{[PdCl4]^{2−}}\). Clearly this cannot be due to any change in the ligand since it is the same in both cases. It is the other factor, the metal, that leads to the difference.

Consider the splitting of the d-orbitals in a generic d⁸ complex. If it were to adopt a square planar geometry, the electrons will be stabilized (with respect to a tetrahedral complex) as they are placed in orbitals of lower energy. However, this comes at a cost: two of the electrons, which were originally unpaired in the tetrahedral structure, are now paired in the square-planer structure:

We can label these two factors as \(ΔE\) (stabilization derived from occupation of lower-energy orbitals) and \(P\) (spin pairing energy) respectively. One can see that:

• If \(ΔE>P\), then the complex will be square planar
• If \(ΔE<P\), then the complex will be tetrahedral.

This is analogous to deciding whether an octahedral complex adopts a high- or low-spin configuration; where the crystal field splitting parameter \(Δ_o\) \(ΔE\) does above. Unfortunately, unlike \(Δ_o\) in octahedral complexes, there is no simple graphical way to represent \(ΔE\) on the diagram above since multiple orbitals are changed in energy between the two geometries.

Interpreting the origin of metal-dependent stabilization energies can be tricky. However, we know experimentally that \(\ce{Pd^{2+}}\) has a larger splitting of the d-orbitals and hence a larger \(\Delta E\) than \(\ce{Ni^{2+}}\) (moreover \(P\) is also smaller).

Practically all 4d and 5d d⁸ \(\ce{ML4}\) complexes adopt a square planar geometry, irrespective if the ligands are strong-field ligand or not. Other examples of such square planar complexes are \(\ce{[PtCl4]^{2−}}\) and \(\ce{[AuCl4]^{-}}\).

Summary

• In tetrahedral molecular geometry, a central atom is located at the center of four substituents, which form the corners of a tetrahedron.
• Tetrahedral geometry is common for complexes where the metal has d⁰ or d¹⁰electron configuration.
• The CFT diagram for tetrahedral complexes has d_x²_−y² and d_z² orbitals equally low in energy because they are between the ligand axis and experience little repulsion.
• In square planar molecular geometry, a central atom is surrounded by constituent atoms, which form the corners of a square on the same plane.
• The square planar geometry is prevalent for transition metal complexes with d⁸ configuration.
• The CFT diagram for square planar complexes can be derived from octahedral complexes yet the dx2-y2 level is the most destabilized and is left unfilled.

Contributors and Attributions

• Angad Oberoi (UCD), Justin Nuckles (UCD)
• StackExchange (orthocresol)