Dilution in Mixing Zones
- Page ID
- 50754
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Is Dilution the Solution to Pollution?
To maintain overall water quality in areas which may experience point source pollution, areas known as mixing zones are sometimes used. The Environmental Protection Agency (EPA) defines a mixing zone as “a limited area or volume of water where initial dilution of a discharge takes place and where numeric water quality criteria can be exceeded but acutely toxic conditions are prevented.” [1]
The EPA has an established list of guidelines for maximum levels of pollutants, including microbial, organic, inorganic, and radioactive substances. States may also institute their own guidelines for mixing zone pollutant levels. The goal of a mixing zone is to have an allocated area of impact where pollutant levels are allowed to exceed the desired or safe limits. Through natural mixing of the polluted water with fresh ambient water, the pollutants should become diluted to acceptable or safe levels by the time the perimeter of the mixing zone is reached. The area in which pollutant concentrations exceed standard limits is referred to as the zone of initial dilution (ZID)[2]. The EPA is seeking to end the use of mixing zones for certain substances which are particularly hazardous or which may bioaccumulate in the food chain.
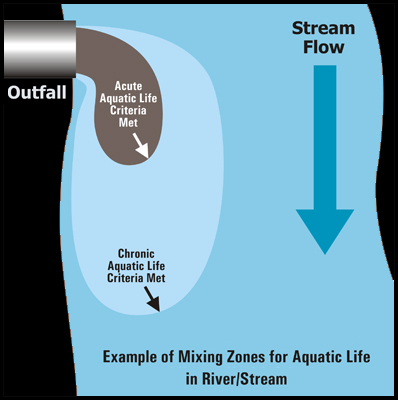
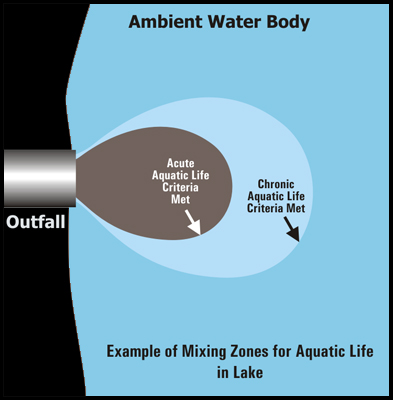
Within the mixing zone, there are different sub regions which vary in concentration of pollutants.
- The criterion maximum concentration (CMC) is the highest acceptable concentration which may be present within the region closest to the pollution point source and represents a concentration at which an organism can be exposed for a brief period of time without experiencing acute affects.
- Farther out is the criterion continuous concentration (CCC) region which is the maximum concentration for a particular pollutant to which an organism can be exposed to indefinitely without experiencing chronic effects.
- The reference ambient concentration (RAC) is the maximum concentration of a pollutant which will not adversely affect human health. All of these concentrations are typically expressed as mg/L.
When comparing an initial solution to one which has been diluted, knowing the initial concentration as well as the initial and final volumes allows for the diluted concentration to be determined.
Example \(\PageIndex{1}\): Concentrations in Mixing Zone
5.80 x 103 L of 0.0271 M formaldehyde is released from the outfall of a textile finishing plant. The designated mixing zone maintains an average volume of 3.5 x 108 L. Assuming equal mixing takes place, what is the concentration of formaldehyde within the mixing zone?
Solution
To determine the concentration of the diluted solution in the mixing zone, we must first determine the amount of formaldehyde (CH2O) present in the concentrated solution:
\(\text{n}_{formaldehyde} = \text{V}_{formaldehyde} \times c_{formaldehyde}\)
\(= \text{5.8} \times \text{10}^3 \text{L} \times \dfrac{\text{0.0271 mol}}{\text{1 L}}\)
\(= \text{157 mol}\)
Dividing the moles of solute by the new volume gives the concentration of the diluted solution:
\( c_{CH_2O} = \dfrac{n_{CH_2O}}{\text{V}}\)
\( c_{CH_2O} = \dfrac{\text{157 mol}}{\text{3.5} \times \text{10}^8 \text{L}}\)
\( c_{CH_2O} = \text{ 4.5} \times \text{10}^{-7} \text{M}\)
The concentration of formaldehyde is diluted to 4.5x10 − 7 M in the mixing zone.
Example \(\PageIndex{2}\):
The Minnesota Pollution Control Agency (MPCA) has set a maximum level for un-iodized ammonia, based on chronic exposure, at 0.016 mg/L of nitrogen from un-ionized ammonia[3]. If 10,500 L of 7.5 mM ammonia is released from an industrial plant, to what volume would it need to be diluted within the mixing zone to achieve an acceptable concentration?
Solution
To solve the problem, the two different expressions of concentration (mg/L and mM) must be converted to the same units. We will convert the 0.016 mg/L of nitrogen to units of mmol/L, or mM.
\(\dfrac{\text{0.016 mg N}}{\text{1 L}} \times \dfrac{\text{1.0 mmol N}}{\text{14.01 mg N}} = \text{0.0011 mmol/L N}\)
Since ammonia, NH3, contains 1 mole of nitrogen per 1 mole of ammonia, the maximum level concentration may be expressed in mM NH3 rather than mM N, giving 0.0011 mM NH3
To determine the total amount of ammonia in the concentrated solution,
\(\text{n}_{ammonia} = \text{V}_{ammonia} \times c_{ammonia}\)
\( = \text{10500 L} \times \dfrac{\text{7.3 mmol}}{\text{1 L}}\)
\( = \text{79000 mmol NH}_3\)
Now determine the volume to which this amount of solute would have to be diluted to reach the desired maximum concentration:
\(\text{V} = \dfrac{n_{NH_3}}{c_{NH_3}}\)
\(\text{V} = \dfrac{\text{79000 mmol}}{\text{0.0011 mmol/L}}\)
\(\text{V}_{NH_3} = \text{7.2} \times \text{10}^7 \text{L}\)
It would take 72 million L of water to dilute to an acceptable concentration within the mixing zone.
Alternate Method
The above calculations can be simplified since concentration and volume are used to calculate the amount of solute present in a solution, and the amount of solute remains constant from a concentrated to diluted solution.
\(\text{n}_{conc} = \text{V}_{conc} \times c_{conc}\)
\(\text{n}_{dil} = \text{V}_{dil} \times c_{dil}\)
Since moles of solute (n) is the same for both the concentrated and diluted solution, then
\( c_{conc} \times \text{V}_{conc} = c_{dil} \times \text{V}_{dil}\)
If we rework Example \(\PageIndex{1}\) using this approach,
\(\text{0.0271 M} \times \text{5.80} \times \text{10}^3 \text{L} = \text{C}_{dil} \times \text{3.5} \times \text{10}^8 \text{L}\)
Solving algebraically for Cdil gives Cdil = 4.5 x 10-7 M
From ChemPRIME: 3.11: Diluting and Mixing Solutions
References
1. “Water Quality Handbook” Chapter 5: General Policies (40 CFR 131.12). Environmental Protection Agency. Retrieved 2011-06-12 http://water.epa.gov/scitech/swguidance/standards/handbook/chapter05.cfm
2. “Water: Mixing Zones” Environmental Protection Agency. Retrieved 2011-06-12. water.epa.gov/scitech/swguida...ones/about.cfm
3. “Water Quality” FM River. Retrieved 2011-06-13. www.eerc.und.nodak.edu/watman/FMRiver/PPTV/ammonia.asp
Contributors and Attributions
Ed Vitz (Kutztown University), John W. Moore (UW-Madison), Justin Shorb (Hope College), Xavier Prat-Resina (University of Minnesota Rochester), Tim Wendorff, and Adam Hahn.


