1.4: The Second Law of Thermodynamics
- Page ID
- 398265
The first law of thermodynamics (Chapter I.2) describes the conservation of energy but does not tell us anything about the direction or spontaneity of a reaction. In this chapter we introduce the concept of entropy as derived by Rudolf Clausius and formulate the second law of thermodynamics. The second law of thermodynamics is of central importance in science and tells us the direction of spontaneous change for any process. We then calculate the change of entropy for a number of exemplary cases.
- Be able to provide a thermodynamic definition of entropy as the reversible heat divided by the temperature.
- Be able to articulate the second law of thermodynamics and understand its meaning and significance: the entropy of the universe increases for all spontaneous processes and the entropy of the universe remains unchanged for an equilibrium (reversible) process.
- Be able to calculate the change in entropy for the compression/expansion of an ideal gas.
- Be able to calculate the change in entropy for the various processes: heating/cooling, phase transition, ideal mixing.
Relevance of the first law of thermodynamics
So far we have been concerning ourselves with the interconversion of heat and work as two form of energy. The first law sets a limit on the magnitude of energy transfer by stating that energy cannot be created or destroyed, thus any change in energy (\(\Delta U\)) must be due to work (\(w\)) or heat (\(q\)) transferred to/from the system with the surroundings.
The mathematical statement of the first law, \(\Delta U = q + w \) is a consequence of the fact that energy is neither created or destroyed but flows from one part of the universe (the system) to another (the surroundings) or is converted from one form to another. Although the first law limits the magnitude of energy change, it says nothing about the directionality of energy transfer or whether or not a process will be spontaneous.
Consider an example sketched in Figure I.4.A. A rubber ball is held some height \(h\) above a table. The ball has some potential energy due to gravity. When the ball is released, its potential energy is converted to kinetic energy, and the ball bounces off the table. Each time the ball bounces, it does not reach the same height as the previous bounce because some of the kinetic energy is being dissipated to the molecules in the table. Eventually, the ball comes to rest, and all its kinetic energy has been transferred to the molecules in the table. This increase in kinetic energy results in the temperature of the table rising, and we can say that the kinetic energy of the ball was converted into heat. This process occurs spontaneously once the ball is dropped and is indicated by the forward arrow labeled a) in Figure I.4.A.
Let’s now consider the reverse process in which the ball at rest on the table absorbs the kinetic energy of the molecules in the table and converts this energy into work by spontaneously levitating against the force of gravity. During this process, the molecules in the table lose some kinetic energy, causing the temperature of the table to decrease. Thus, heat has been converted to work needed to raise the ball to some height \(h\). This process is indicated by the reverse arrow labeled b) in Figure I.4.A.
In both cases, the total energy is conserved in compliance with the first law of thermodynamics, but the first process occurs spontaneously, while the second process does not occur spontaneously. For the second process to occur, all the molecules in the table would need to spontaneously synchronize their random motion and transfer their kinetic energy to the ball. If there are sufficiently many molecules in the table, the probability for these molecules to synchronize their random motion is extremely unlikely. The second law of thermodynamics will set a limit on the direction of energy transfer, such that case 1 (potential energy → kinetic energy → heat) is spontaneous, but that the reverse process, case 2 (heat → kinetic energy → potential energy), will not happen.
Thermodynamic Definition of Entropy
In this chapter we consider the thermodynamic definition of entropy as formulated by Rudolf Clausius (1822-1888). Let’s consider again the reversible heat transfer of a system going from some initial state (P1, T1, V1) to some final state (P2, T2, V2). From the first law of thermodynamics we have \(dU = \delta w + \delta q_{rev}\) where the subscript on \(\delta q_{rev}\) indicates that the heat transfer we are considering is for a reversible process. Recall that both work and heat are not state properties and thus depend on the path taken. For reversible work we know that \(\delta w = -P \cdot dV\). Also, we have that \(dU = C_v \cdot dT\) from Chapter I.2 (See Equation I.2.31). Inserting these into the equation for the first law (Equation I.2.9) and solving for the unknown \(\delta q_{rev}\), we have:
\[\delta q_{rev} = C_v \cdot dT + P \cdot dV\label{EQ:heat_rev}\]
Equation \ref{EQ:heat_rev} is an expression for the reversible heat. Integrating both sides of Equation \ref{EQ:heat_rev} from an initial state \(i\) to a final state \(f\):
\[q_{rev} = C_v \Delta T +\int_i^f P \cdot dV\label{EQ:heat_rev2}\]
We see that the reversible heat depends on the path due to the work term \(P \cdot dV\). This is not surprising because the heat is not a state property.
Following Clausius, let’s now consider a slightly different quality \(\frac{\delta q_{rev}}{T}\). From Equation \ref{EQ:heat_rev}, dividing both side by \(T\), we have:
\[\frac{\delta q_{rev}}{T} = C_v \cdot \frac{dT}{T} + \frac{P}{T} \cdot dV\label{EQ:entropy1}\]
Using the fact that \(\frac{P}{T}=\frac{nR}{V}\) for an ideal gas, we can integrate both sides of Equation \ref{EQ:entropy1} independently of the path!
\[\begin{eqnarray}\int_i^f \frac{\delta q_{rev}}{T} &=& C_v \int_i^f \frac{dT}{T} + nR \int_i^f \frac{dV}{V} \nonumber \\[4pt] &=& C_v \ln \left(\frac{T_f}{T_i}\right) + nR \ln \left(\frac{V_f}{V_i}\right)\label{EQ:entropy2}\end{eqnarray}\]
Therefore, we conclude that the quantity \(\frac{\delta q_{rev}}{T}\) is a state property! We define this new state property \(\bf{S}\), so that:
\[dS = \frac{\delta q_{rev}}{T}\label{EQ:entropy_def1}\]
and, integrating both sides from an initial state \(i\) to a final state \(f\):
\[\int_i^f dS = \int_i^f \frac{\delta q_{rev}}{T} = \Delta S\label{EQ:entropy_def2}\]
where \(\Delta S= S_f – S_i \). The state property \(\bf{S}\) is called the entropy.
Key Result: The infinitesimal change in entropy is defined as \(dS = \frac{\delta q_{rev}}{T}\). Notice the entropy is defined in terms of the reversible heat.
From Equation \ref{EQ:entropy2} and Equation I.4.\ref{EQ:entropy_def2} we have that for the expansion of an ideal gas, the change in entropy is:
\[
\Delta S = C_v \ln \left(\frac{T_2}{T_1}\right) + nR \ln \left(\frac{V_2}{V_1}\right)
\label{EQ:deltaS_gas}
\]
Notice that Equation \ref{EQ:deltaS_gas} is valid for any expansion/compression of an ideal gas regardless of whether the process was carried our reversibly or irreversibly because entropy is a state property.
Key Result: The change in entropy for the reversible or irreversible expansion/compression of an ideal gas is: \(\Delta S = C_v \ln \left(\frac{T_2}{T_1}\right) + nR \ln \left(\frac{V_2}{V_1}\right)\)
Note: Clausius was able to find a new state property by dividing the reversible heat \(\bf{\delta q_{rev}}\) (not a state property) by the temperature. The temperature in this case is called an integrating factor that makes the integral \(\int \frac{\delta q_{rev}}{T}\) exact.
Entropy for an irreversible vs. reversible process
So far, we have defined \(\bf{dS}\) from Equation \ref{EQ:entropy_def1} in terms of the reversible heat \(\bf{\delta q_{rev}}.\) Note that the subscript rev indicates the process is reversible. While the entropy is a state property (independent of the path), the heat is not and will depend on the path. Therefore, the equivalence in Equation \ref{EQ:entropy_def1} is valid only for a reversible path. Even though the entropy is the same, the magnitude of the heat transfer is greater for the reversible process, so we have:
\[\delta q_{rev} > \delta q_{irrev}\label{EQ:q_relation}\]
Dividing both sides of Equation \ref{EQ:q_relation} by \(\bf{T}\) and inserting the definition of entropy from Equation I.4.\ref{EQ:entropy_def1} gives:
\[dS > \frac{\delta q_{irrev}}{T}\label{EQ:entropy_irrev}\]
While the entropy change would be the same for an irreversible or reversible process, \(\Delta S = \Delta S_{rev} = \Delta S_{irrev}\), the heat flow is not the same, so for any irreversible process \(\Delta S > q_{irrev}/T\).
Key Result: For any process the change in entropy is \( dS \ge \frac{\delta q}{T}.\) The equality holds only for a reversible process, whereas the inequality holds if the process is irreversible.
Entropy of the Surroundings
So far we have only focused on the entropy of the system. In this section we will consider the change in entropy of the surroundings. First, we notice that any heat gained (or lost) by the system must have come from (or gone to) the surroundings:
\[\delta q_{sys} = – \delta q_{surr}\label{EQ:qsurr}\]
We consider the surroundings as an infinitely large reservoir. Any amount of heat transferred to the surroundings (\(\delta q_{surr}\)) will only lead to an infinitesimally small change in the reservoir, given that the reservoir is sufficiently large. Infinitesimally small changes are characteristic of a reversible process, so any heat transfer from the perspective of the surroundings can be treated as reversible, since it will have the same effect on the surroundings as a reversible process. Thus, from Equation I.4.\ref{EQ:entropy_def1}, we can always write for the surroundings:
\[dS_{surr} = \frac{\delta q_{surr}}{T}\label{EQ:dS_surr}\]
or
\[\Delta S_{surr} = \frac{q_{surr}}{T}\label{EQ:S_surr}\]
The Second Law of Thermodynamics
The Second Law of Thermodynamics deals with the change in entropy of the universe. The change of entropy of the universe is:
\[\Delta S_{universe}=\Delta S_{sys} + \Delta S_{surr}\label{EQ:DeltaS_universe}\]
Substituting Equation \ref{EQ:S_surr} into Equation \ref{EQ:DeltaS_universe} gives:
\[\Delta S_{universe}=\Delta S_{sys} + \frac{q_{surr}}{T}\label{EQ:DeltaS_universe2}\]
For a reversible process we can substitute the equality of Equation \ref{EQ:entropy_def1} to give:
\[\begin{eqnarray}\Delta S_{universe}&=&\frac{q_{rev}}{T} + \frac{q_{surr}}{T} \nonumber \\[4pt] \Delta S_{universe}&=& 0\label{EQ:DeltaS_universe3}\end{eqnarray}\]
where the last line follows from the fact that the heat gained by the surroundings is equal and opposite to the heat lost by the system (\(q_{sys}= -q_{surr}\)). We see that for a reversible process the change of entropy of the universe is zero.
Now, if the processes is irreversible we have to use the inequality of Equation \ref{EQ:entropy_irrev}. Substituting this into Equation I.4.\ref{EQ:DeltaS_universe2} gives for an irreversible processes:
\[\begin{eqnarray}\Delta S_{universe} &>& \frac{q_{rev}}{T} + \frac{q_{surr}}{T} \nonumber \\[4pt] \Delta S_{universe} &>& 0\label{EQ:DeltaS_universe4}\end{eqnarray}\]
where again the last line follows from the fact that the heat gained by the surroundings is equal and opposite to the heat lost by the system (\(q_{sys}= -q_{surr}\)). Thus, for an irreversible process, the change in entropy of the universe must be greater than zero.
This result is known as the Second Law of Thermodynamics which can be expressed in mathematical form as:
\[\Delta S_{universe} \ge 0\label{EQ:secondlaw}\]
Where the equality holds if the process is reversible, and the inequality applies if the process is irreversible.
Key Result: The entropy of an isolated system always increases in an irreversible process and remains unchanged in a reversible process. It can never decrease. This statement is known as the second law of thermodynamics and is expressed mathematically as: \(\Delta S_{universe} \ge 0\)
See Practice Problem 1
Some applications of calculating the entropy
Having defined the second law of thermodynamics, we will now consider some specific examples of calculating \(\Delta S\).
Example 1: Cyclic process
A cyclic process is any series of steps that returns the system to its original state. Because entropy is a state property:
\[\Delta S = \sum_i \Delta S_i = 0\label{EQ:Scyclic}\]
where \(\Delta S_i\) is the entropy change for the \(ith\) step and the change in entropy for the cycle is zero because S is a state property.
Example 2: Reversible adiabatic process
An adiabatic process is a process in which no heat is exchanged between the system and surroundings. For a reversible adiabatic processes, \(\delta q_{rev}=0\) since no heat is exchanged. Integrating Equation \ref{EQ:entropy_def1} gives:
\[\begin{eqnarray}\Delta S &=& \int \frac{\delta q_{rev}}{T} \nonumber \\[4pt] \Delta S &=& 0\end{eqnarray}\]
where the second line follows for an adiabatic process (\(\delta q_{rev}=0\)).
Example 3: Reversible phase change at constant T and P
At the phase transition temperature, both the forward and reverse reactions are in equilibrium. Therefore, at precisely the phase transition temperature, the phase transition is reversible. For example, the freezing of liquid water is reversible (at equilibrium) at the phase transition temperature of 0 °C.
H2O (l) ↔ H2O (s) T = 0 °C
From Equation \ref{EQ:entropy_def1} at constant T we can write:
\[\Delta S = \frac{q_{rev}}{T}\]
Recalling, that under constant pressure conditions, \(q_p = \Delta H\), we can write, for a reversible phase transition:
\[\Delta S = \frac{\Delta H}{T}\]
where \(\Delta H\) is the change in enthalpy of the associated phase transition.
Example 4: Constant pressure (reversible) heating (no phase change)
Consider heating a substance from some initial temperature \(\bf{T_i}\) to some final temperature \(\bf{T_f}\) reversibly. We assume that there are no phase transitions between \(\bf{T_i}\) and \(\bf{T_f}\). At constant pressure, we begin with the definition of the heat capacity:
\[\delta q = C_p \cdot dT\label{EQ:heatcapacity}\]
Substituting Equation \ref{EQ:heatcapacity} into the definition of the entropy, Equation \ref{EQ:entropy_def1} gives:
\[\begin{eqnarray}\Delta S &=& \int_{T_i}^{T_f} C_p \frac{dT}{T} \nonumber \\[4pt] \Delta S &=& C_p \int_{T_i}^{T_f}\frac{dT}{T} \nonumber \\[4pt] \Delta S &=& C_p \ln \left(\frac{T_f}{T_i}\right) \nonumber \\\label{EQ:entropyheating}\end{eqnarray}\]
where we have assumed the heat capacity \(\bf{C_p}\) is independent of temperature.
See Practice Problem 2
Example 5: Ideal mixing of two inert gases at constant T and P
In this example, we consider the mixing of two ideal gases. Consider the situation shown in Figure I.4.B. Two gases of different chemical identities A and B are contained in two flasks of volume \(V_A\) and \(V_B\). Let \(n_A\) be the number of moles of gas A, and \(n_B\) be the number of moles of gas B. When the stopcock separating the two flasks is open, the gases will spontaneously mix so that both gases fill the final volume of \(V=V_A + V_B\). Similarly, the total number of moles of the combined system is \(n=n_A + n_B\).
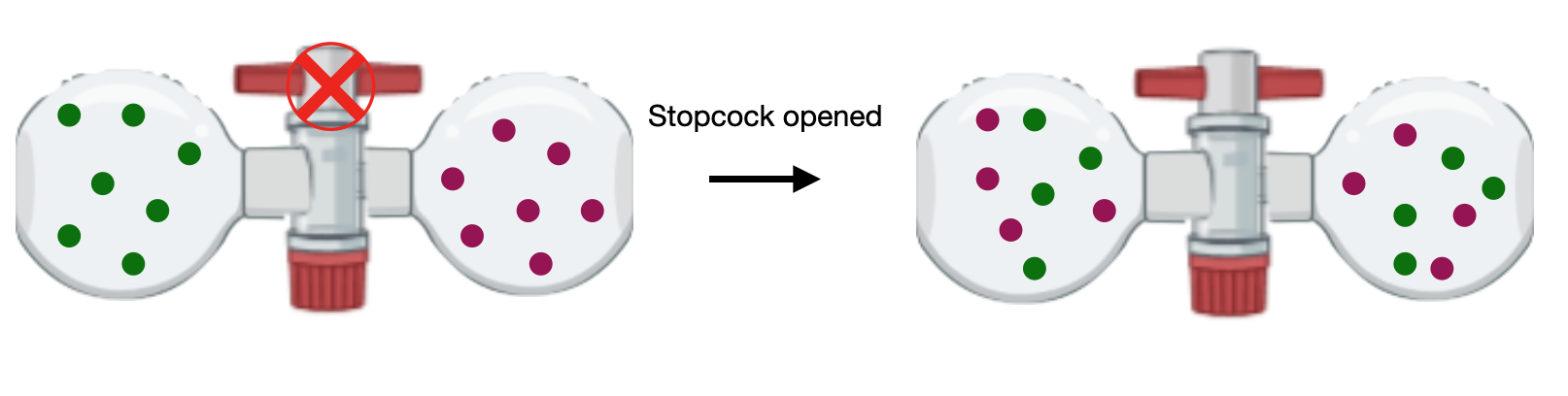
The overall change in entropy for the mixing of two gases is the sum of the change in entropy for each gas:
\[\Delta S = \Delta S_A + \Delta S_B\label{EQ:DeltaS_mix1}\]
At constant \(\bf{T}\), the entropy change for gas A is given by the second term in Equation \ref{EQ:deltaS_gas}:
\[\Delta S_A = n_A R \ln \left(\frac{V}{V_A}\right)\label{EQ:DeltaS_A}\]
and similarly for gas B:
\[\Delta S_B = n_B R \ln \left(\frac{V}{V_B}\right)\label{EQ:DeltaS_B}\]
Substituting Equation \ref{EQ:DeltaS_A} and Equation \ref{EQ:DeltaS_B} into Equation I.4.\ref{EQ:DeltaS_mix1} gives:
\[\Delta S = n_A R \ln \left(\frac{V}{V_A}\right)+ n_B R \ln \left(\frac{V}{V_B}\right)\label{EQ:DeltaS_mix2}\]
Using the fact that the total volume is \(V=nRT/P\) for an ideal gas, Equation \ref{EQ:DeltaS_mix2} becomes:
\[\begin{eqnarray}\Delta S &=& -n_A R \ln \left(\frac{n_A}{n}\right)- n_B R \ln \left(\frac{n_B}{n}\right) \nonumber \\[4pt] \Delta S &=& -n_A R \ln \left(x_A \right)- n_B R \ln \left(x_B \right)\label{EQ:DeltaS_mix3}\end{eqnarray}\]
where \(x_A\) is the mole fraction of gas A defined as \(x_A = n_A/n\) and \(x_B\) is the mole fraction of gas B. Notice that because the mole fraction is less than one, \(\Delta S\) for mixing of two ideal gases is be greater than zero.
See Practice Problem 3
Examples
What is the change in entropy when one mole of liquid water is heated from its freezing point to its boiling point in an open container. The molar heat capacity of liquid water is 75.38 J mol\(^{-1}\) K\(^{-1}\).
Solution
Since the water is being heated at constant pressure, we use Equation \ref{EQ:entropyheating}:
\(\Delta S=C_p \ln \left(\frac{T_f}{T_i}\right) \)
or, after introducing the definition of the molar heat capacity:
\(\Delta S=n \bar{C_p} \ln \left(\frac{T_f}{T_i}\right) \)
Substituting in the values of the initial and final temperatures gives:
\(\Delta S=1 \ \text{mole} \ \times \ 75.38 \ \text{J mol}^{-1} \ \text{K}^{-1} \ \ln \left(\frac{373.15 \ \text{K}}{273.15 \ \text{K}}\right) \)
\(\Delta S = 23.52 \ \text{J K}^{-1} \)
Notice that the entropy increases upon heating.
Show that for a reversible adiabatic expansion of an ideal gas \(\Delta S = 0 \), but for an irreversible adiabatic expansion of an (isolated) ideal gas \(\Delta S > 0 \)
Solution
For a reversible process, (see Example 2), we have from the definition of the entropy:
\( \Delta S = \int \frac{\delta q_{rev}}{T} \)
Since the process is adiabatic, there is no heat exchange with the surroundings, meaning that \(q_{rev} = 0 \) and
\( \Delta S = 0\)
For an irreversible process, we have from Equation \ref{EQ:entropy_irrev}:
\( \Delta S > \int \frac{\delta q_{irrev}}{T} \)
Again, the process is adiabatic so there is no heat exchange with the surroundings, meaning that \(q_{irrev} = 0 \), giving:
\( \Delta S > 0 \)
Note that this result applies only to an isolated system. It is possible to reduce the entropy of the system with the aid of the external surroundings. The entropy change of both system + surroundings taken together, however, cannot decrease.
Practice Problems
Problem 1. One mole of an ideal gas is isothermally expanded from 5.0 L to 10 L at 300 K. Compare the entropy changes for the system, surroundings, and the universe if the process is carried out a) reversibly, and b) irreversibly against a constant external pressure of 2.0 atm.
Problem 2. The molar enthalpy of vaporization of water is \(\Delta H_{vap}=40.6\) kJ/mol at the boiling temperature of 100 °C. a) What is the value of \(\Delta S\) when one mole of liquid water is converted to a gas at 100 °C. b) What is \(\Delta S\) for the conversion of one mole of liquid water to a gas at a temperature of 120 °C. The molar heat capacity of liquid water is 75.38 J mol\(^{-1}\) K\(^{-1}\) and the molar heat capacity of water vapor is 36.57 J mol\(^{-1}\) K\(^{-1}\).
Hint consider \(\Delta S\) of heating/cooling from Example 4 (see Example 1.4.1) in addition to \(\Delta S\) for a phase transition in Example 3.
Problem 3. Suppose you have a compartment that contains 1 mole of NO and a second compartment that contains 0.3 moles of O2. Calculate the change in entropy \(\Delta S\) of mixing the two gasses together. Assume the gasses do not react and are ideal gasses.