4.5: Characteristics of Molecules
- Page ID
- 83070
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Skills to Develop
- Determine the molecular mass of a molecule.
- Predict the general shape of a simple covalent molecule.
Unlike the ions in ionic compounds, which are arranged in lattices called crystals, molecules of covalent compounds exist as discrete units with a characteristic mass and a certain three-dimensional shape.
Molecular Mass
The mass of a molecule — the molecular mass — is simply the sum of the masses of its atoms. As with formula masses, it is important that you keep track of the number of atoms of each element in the molecular formula to obtain the correct mass. For molecules, molecular mass and formula mass mean the same thing. Ionic compounds, however, do not involve molecules and thus formula mass is technically the only appropriate term. In practice, the terms molecular mass, formula mass, and even molecular weight or formula weight are used interchangeably.
Example \(\PageIndex{1}\)
What is the molecular mass of each covalent compound?
- H2O
- C6H6
- NO2
- N2O5
SOLUTION
Use the masses of the atoms from the Periodic Table.
The molecular formula H2O indicates that there are two hydrogen atoms and one oxygen atom in each molecule. Summing the masses of these atoms,
| 2 H: | 2 × 1.01 = | 2.02 u |
| 1 O: | + 16.00 u | |
| Total: | 18.02 u |
The molecular mass of H2O is 18.02 u.
| 6 C: | 6 × 12.01 = | 72.06 u |
| 6 H: | 6 × 1.01 = | + 6.06 u |
| Total: | 78.12 u |
The molecular mass of C6H6 is 78.12 u.
| 1 N: | 14.01 u | |
| 2 O: | 2 × 16.00 = | + 32.00 u |
| Total: | 46.01 u |
The molecular mass of NO2 is 46.01 u.
| 2 N: | 2 × 14.01 = | 28.02 u |
| 5 O: | 5 × 16.00 = | + 80.00 u |
| Total: | 108.02 u |
The molecular mass of N2O5 is 108.02 u.
Note that the two different nitrogen and oxygen compounds in these examples have different molecular masses.
Molecular Shape: VSEPR Theory
Unlike ionic compounds, with their extended crystal lattices, covalent molecules are discrete units with specific three-dimensional shapes. The shape of a molecule is determined by the fact that negative electrons tend to repel one another. The electron groups on the central atom of a molecule tend to spread out as far apart as possible. This concept is called the valence shell electron pair repulsion (VSEPR) theory. Electron groups can be covalent bonds or lone pairs on the central atom. For example, the best way to minimize repulsions between the two bonds in BeCl2 is if they are on opposite sides, ending up 180° apart from each other. The result is a linear molecule:

Linear molecules are often described as having an AB2 molecular type, where A represents the central atom and each B represents other atoms covalently bonded to the central atom (subscript indicating how many).
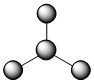
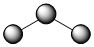
The three covalent bonds in BF3 repel each other to form 120° angles in a flat plane. This AB3 molecular type makes a shape called trigonal planar:

The BeCl2 and BF3 molecules shown above actually violate the octet rule; however, such exceptions are rare and will not be discussed in this text.
When using VSEPR theory, double and triple bonds are treated no differently than single bonds. For example, formaldehyde (H2CO) is also AB3 because three atoms — H, H & O — are bonded to the central carbon atom, and it also has a trigonal planar shape.

Note
Try sticking three toothpicks into a marshmallow or a gumdrop and see if you can find different positions where your “bonds” are farther apart than the planar 120° orientation.
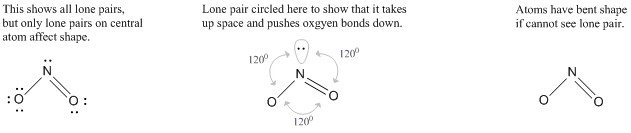
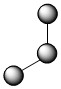
Molecules with lone electron pairs around the central atom have a shape based on the repulsion between both the bonds and the lone pairs on that central atom. The nitrite ion (NO2–), a common food preservative, is an example. The central nitrogen has one lone electron pair and two bonded electron pairs. The molecular type here would be AB2E, where the E represents a lone pair. These three electron pairs repel each other and adopt a trigonal planar arrangement with 1200 angles between them:
.jpg?revision=1)
However, the shape of the molecule is described in terms of the positions of the atoms, not the lone electron pairs. Thus, NO2– is said to have a bent shape, not a trigonal planar one. It is assumed that the lone pair is "invisible" when describing the shape of the molecular geometry. The lone pair pushes the bonds to oxygen down in the figure above, making it appear bent.
The four covalent bonds in CCl4 have AB4 molecular type and arrange themselves three dimensionally, not flat. The best way to spread four groups as far apart as possible is with 109.5° angles and the shape is described as tetrahedral.
.jpg?revision=2&size=bestfit&width=950)
In the image above, the regular lines are meant to represent bonds that are flat against the plane of the page. The solid wedge represents a bond that is coming up from the page (toward you). The hatched wedge, also sometimes shown as just a dashed line, represents a bond going into the plane of the page (away from you).
Ammonia (NH3) has one lone electron pair and three bonded electron pairs. The molecular type here would be AB3E, where the E represents a lone pair. These four electron pairs repel each other and adopt a tetrahedral arrangement:
.jpg?revision=1)

The angles are again about 109.50, but NH3 is said to have a trigonal pyramidal shape, not a tetrahedral one. The lone pair in NH3 pushes the bonds to hydrogen down to the bottom of the pyramid in the figure above, making a triangular base. Assuming the lone pair is "invisible" when describing the shape, the nitrogen would be the top of the pyramid in the figure.
SIDE NOTE: Because bonds and lone pairs are not always the same size, they do not repel equally. This means the angles might vary slightly. In this course, we will not be concerned with these small differences. Instead, assume the angles will be approximately one of three choices: 1800, 1200, or 109.50.
Water (H2O) is molecular type AB2E2 with two lone pairs of electrons around the central oxygen atom, in addition to the two bonded pairs:
.jpg?revision=1)
Although the four electron pairs adopt a tetrahedral arrangement due to repulsion, again the shape of the molecule is described by the positions of the atoms only. If the lone pairs are assumed invisible, the shape of H2O appears bent. Both AB3E and AB2E2 have close to 109.50 angles because that is the best way to spread out four electron groups.
In determining the shapes of molecules, it is important to first draw the Lewis diagram for a molecule. Only the correct Lewis structure will show how many bonds and lone pairs are associated with the central atom in the molecule, both necessary to predict shape. It is important to note that the first Lewis diagrams you draw (or the one given in in a problem) might not have the correct 3D geometry — you must be able to predict the shape and angles based on the diagram. The table below summarizes the most common molecular geometries. (There are more, but they will not be covered in this course.)
|
Electron Groups (see Note #1) |
Bonding Groups (see Note #2) |
Lone Pairs (see Note #3) |
Molecular Type (ABxEy) |
Molecular Geometry (Shape Name) |
Bond Angles (Approximate) |
Example Lewis Structure Diagram |
Example 3D Shape (See Note # 4) |
| 2 | 2 | 0 | AB2 | linear | 1800 | H — C ≡ N: | .jpg?revision=2&size=bestfit&width=100) |
| 3 | 3 | 0 | AB3 | trigonal planar | 1200 | .jpg?revision=1) |
.jpg?revision=1) |
| 3 | 2 | 1 | AB2E | bent | 1200 | 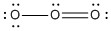.jpg?revision=1&size=bestfit&width=135&height=35) |
.jpg?revision=2&size=bestfit&height=50) |
| 4 | 4 | 0 | AB4 | tetrahedral | 109.50 | 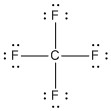.jpg?revision=1&size=bestfit&width=115&height=115) |
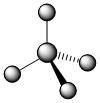.jpg?revision=1) |
| 4 | 3 | 1 | AB3E | trigonal pyramidal | 109.50 | 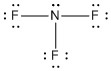.jpg?revision=1) |
.jpg?revision=1) |
| 4 | 2 | 2 | AB2E2 | bent | 109.50 | .jpg?revision=1) |
2.jpg?revision=1) |
NOTE #1: Electron groups can be covalent bonds or lone pairs.
NOTE #2: Double or triple bonds each count only as one electron group, so are treated just like single bonds.
NOTE #3: Each lone pair (two dots) counts as one electron group, but only if it is located on the central atom.
NOTE #4: When describing the shape for molecular geometry, any lone pairs are considered invisible.
Example \(\PageIndex{2}\)
Describe the shape of each molecule.
- PCl3
- CO2
SOLUTION
-
The Lewis diagram for PCl3 is as follows:

The four electron pairs arrange themselves tetrahedrally, but the lone electron pair is not considered in describing the molecular shape. Like NH3, this molecule is trigonal pyramidal. (Notice that the bond angles in the Lewis structure are drawn flat and at 900 angles; the actual pyramidal shape is not flat and has angles of about 109.50.
-
The Lewis diagram for CO2 is as follows:
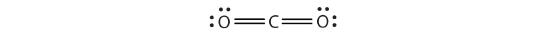
The multiple bonds are treated as one group. Thus, CO2 has only two groups of electrons that repel each other. They will direct themselves 180° apart from each other, so CO2 molecules are linear.
Concept Review Exercises
- How do you determine the molecular mass of a covalent compound?
- How do you determine the shape of a molecule?
Answers
-
The molecular mass is the sum of the masses of the atoms in the formula.
-
The shape of a molecule is determined by the position of the atoms, which in turn is determined by the repulsion of the bonded and lone electron pairs around the central atom.
Key Takeaways
- A molecule has a certain mass, called the molecular mass.
- Simple molecules have geometries that can be determined from VSEPR theory.
Exercises
-
What is the molecular mass of each compound?
- HCl
- N2O4
- ICl3
- Aspirin (C9H8O4)
-
What is the shape of each molecule? (Hint: First draw the Lewis diagram of each.)
- H2S
- COCl2
- SO2
-
Predict the shape of nitrous oxide (N2O), which is used as an anesthetic. A nitrogen atom is in the center of this three-atom molecule.
Answers
-
- 36.46 u
- 92.02 u
- 233.25 u
- 180.17 u
- bent
- trigonal planar
- bent
3. linear
Contributors
- Anonymous

