11.8: Bonding in Solids
- Page ID
- 91239
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Learning Objectives
- To understand the correlation between bonding and the properties of solids.
- To classify solids as ionic, molecular, covalent (network), or metallic, where the general order of increasing strength of interactions.
Crystalline solids fall into one of four categories. All four categories involve packing discrete molecules or atoms into a lattice or repeating array, though network solids are a special case. The categories are distinguished by the nature of the interactions holding the discrete molecules or atoms together. Based on the nature of the forces that hold the component atoms, molecules, or ions together, solids may be formally classified as ionic, molecular, covalent (network), or metallic. The variation in the relative strengths of these four types of interactions correlates nicely with their wide variation in properties.
| Type of Solid | Interaction | Properties | Examples |
|---|---|---|---|
| Ionic | Ionic | High Melting Point, Brittle, Hard | NaCl, MgO |
| Molecular | Hydrogen Bonding, Dipole-Dipole, London Dispersion |
Low Melting Point, Nonconducting | H2, CO2 |
| Metallic | Metallic Bonding | Variable Hardness and Melting Point (depending upon strength of metallic bonding), Conducting | Fe, Mg |
| Network | Covalent Bonding | High Melting Point, Hard, Nonconducting | C (diamond), SiO2 (quartz) |
In ionic and molecular solids, there are no chemical bonds between the molecules, atoms, or ions. The solid consists of discrete chemical species held together by intermolecular forces that are electrostatic or Coulombic in nature. This behavior is most obvious for an ionic solid such as \(NaCl\), where the positively charged Na+ ions are attracted to the negatively charged \(Cl^-\) ions. Even in the absence of ions, however, electrostatic forces are operational. For polar molecules such as \(CH_2Cl_2\), the positively charged region of one molecular is attracted to the negatively charged region of another molecule (dipole-dipole interactions). For a nonpolar molecule such as \(CO_2\), which has no permanent dipole moment, the random motion of electrons gives rise to temporary polarity (a temporary dipole moment). Electrostatic attractions between two temporarily polarized molecules are called London Dispersion Forces.
Hydrogen bonding is a term describing an attractive interaction between a hydrogen atom from a molecule or a molecular fragment X–H in which X is more electronegative than H, and an atom or a group of atoms in the same or a different molecule, in which there is evidence of bond formation. (See the IUPAC Provisional Recommendation on the definition of a hydrogen bond.) Dots are employed to indicate the presence of a hydrogen bond: X–H•••Y. The attractive interaction in a hydrogen bond typically has a strong electrostatic contribution, but dispersion forces and weak covalent bonding are also present.
In metallic solids and network solids, however, chemical bonds hold the individual chemical subunits together. The crystal is essential a single, macroscopic molecule with continuous chemical bonding throughout the entire structure. In metallic solids, the valence electrons are no longer exclusively associated with a single atom. Instead these electrons exist in molecular orbitals that are delocalized over many atoms, producing an electronic band structure. The metallic crystal essentially consists of a set of metal cations in a sea of electrons. This type of chemical bonding is called metallic bonding.
Ionic Solids
You learned previously that an ionic solid consists of positively and negatively charged ions held together by electrostatic forces. The strength of the attractive forces depends on the charge and size of the ions that compose the lattice and determines many of the physical properties of the crystal.
The lattice energy (i.e., the energy required to separate 1 mol of a crystalline ionic solid into its component ions in the gas phase) is directly proportional to the product of the ionic charges and inversely proportional to the sum of the radii of the ions. For example, NaF and CaO both crystallize in the face-centered cubic (fcc) sodium chloride structure, and the sizes of their component ions are about the same: Na+ (102 pm) versus Ca2+ (100 pm), and F− (133 pm) versus O2− (140 pm). Because of the higher charge on the ions in CaO, however, the lattice energy of CaO is almost four times greater than that of NaF (3401 kJ/mol versus 923 kJ/mol). The forces that hold Ca and O together in CaO are much stronger than those that hold Na and F together in NaF, so the heat of fusion of CaO is almost twice that of NaF (59 kJ/mol versus 33.4 kJ/mol), and the melting point of CaO is 2927°C versus 996°C for NaF. In both cases, however, the values are large; that is, simple ionic compounds have high melting points and are relatively hard (and brittle) solids.
Molecular Solids
Molecular solids consist of atoms or molecules held to each other by dipole–dipole interactions, London dispersion forces, or hydrogen bonds, or any combination of these. The arrangement of the molecules in solid benzene is as follows:

The structure of solid benzene. In solid benzene, the molecules are not arranged with their planes parallel to one another but at 90° angles.
Because the intermolecular interactions in a molecular solid are relatively weak compared with ionic and covalent bonds, molecular solids tend to be soft, low melting, and easily vaporized (\(ΔH_{fus}\) and \(ΔH_{vap}\) are low). For similar substances, the strength of the London dispersion forces increases smoothly with increasing molecular mass. For example, the melting points of benzene (C6H6), naphthalene (C10H8), and anthracene (C14H10), with one, two, and three fused aromatic rings, are 5.5°C, 80.2°C, and 215°C, respectively. The enthalpies of fusion also increase smoothly within the series: benzene (9.95 kJ/mol) < naphthalene (19.1 kJ/mol) < anthracene (28.8 kJ/mol). If the molecules have shapes that cannot pack together efficiently in the crystal, however, then the melting points and the enthalpies of fusion tend to be unexpectedly low because the molecules are unable to arrange themselves to optimize intermolecular interactions. Thus toluene (C6H5CH3) and m-xylene [m-C6H4(CH3)2] have melting points of −95°C and −48°C, respectively, which are significantly lower than the melting point of the lighter but more symmetrical analog, benzene.
Self-healing rubber is an example of a molecular solid with the potential for significant commercial applications. The material can stretch, but when snapped into pieces it can bond back together again through reestablishment of its hydrogen-bonding network without showing any sign of weakness. Among other applications, it is being studied for its use in adhesives and bicycle tires that will self-heal.

Toluene and m-xylene. The methyl groups attached to the phenyl ring in toluene and m-xylene prevent the rings from packing together as in solid benzene.
Covalent Network Solids
Covalent solids are formed by networks or chains of atoms or molecules held together by covalent bonds. A perfect single crystal of a covalent solid is therefore a single giant molecule. For example, the structure of diamond, shown in part (a) in Figure \(\PageIndex{1}\), consists of sp3 hybridized carbon atoms, each bonded to four other carbon atoms in a tetrahedral array to create a giant network. The carbon atoms form six-membered rings.

The unit cell of diamond can be described as an fcc array of carbon atoms with four additional carbon atoms inserted into four of the tetrahedral holes. It thus has the zinc blende structure described in Section 12.3, except that in zinc blende the atoms that compose the fcc array are sulfur and the atoms in the tetrahedral holes are zinc. Elemental silicon has the same structure, as does silicon carbide (SiC), which has alternating C and Si atoms. The structure of crystalline quartz (SiO2), shown in Section 12.1, can be viewed as being derived from the structure of silicon by inserting an oxygen atom between each pair of silicon atoms.
All compounds with the diamond and related structures are hard, high-melting-point solids that are not easily deformed. Instead, they tend to shatter when subjected to large stresses, and they usually do not conduct electricity very well. In fact, diamond (melting point = 3500°C at 63.5 atm) is one of the hardest substances known, and silicon carbide (melting point = 2986°C) is used commercially as an abrasive in sandpaper and grinding wheels. It is difficult to deform or melt these and related compounds because strong covalent (C–C or Si–Si) or polar covalent (Si–C or Si–O) bonds must be broken, which requires a large input of energy.
Other covalent solids have very different structures. For example, graphite, the other common allotrope of carbon, has the structure shown in part (b) in Figure \(\PageIndex{1}\). It contains planar networks of six-membered rings of sp2 hybridized carbon atoms in which each carbon is bonded to three others. This leaves a single electron in an unhybridized 2pz orbital that can be used to form C=C double bonds, resulting in a ring with alternating double and single bonds. Because of its resonance structures, the bonding in graphite is best viewed as consisting of a network of C–C single bonds with one-third of a π bond holding the carbons together, similar to the bonding in benzene.
To completely describe the bonding in graphite, we need a molecular orbital approach similar to the one used for benzene in Chapter 9. In fact, the C–C distance in graphite (141.5 pm) is slightly longer than the distance in benzene (139.5 pm), consistent with a net carbon–carbon bond order of 1.33. In graphite, the two-dimensional planes of carbon atoms are stacked to form a three-dimensional solid; only London dispersion forces hold the layers together. As a result, graphite exhibits properties typical of both covalent and molecular solids. Due to strong covalent bonding within the layers, graphite has a very high melting point, as expected for a covalent solid (it actually sublimes at about 3915°C). It is also very soft; the layers can easily slide past one another because of the weak interlayer interactions. Consequently, graphite is used as a lubricant and as the “lead” in pencils; the friction between graphite and a piece of paper is sufficient to leave a thin layer of carbon on the paper. Graphite is unusual among covalent solids in that its electrical conductivity is very high parallel to the planes of carbon atoms because of delocalized C–C π bonding. Finally, graphite is black because it contains an immense number of alternating double bonds, which results in a very small energy difference between the individual molecular orbitals. Thus light of virtually all wavelengths is absorbed. Diamond, on the other hand, is colorless when pure because it has no delocalized electrons. Table \(\PageIndex{2}\) compares the strengths of the intermolecular and intramolecular interactions for three covalent solids, showing the comparative weakness of the interlayer interactions.
| Substance | ΔHsub (kJ/mol) | Average Bond Energy (kJ/mol) |
|---|---|---|
| phosphorus (s) | 58.98 | 201 |
| sulfur (s) | 64.22 | 226 |
| iodine (s) | 62.42 | 149 |
Carbon: An example of an Covalent Network Solid
In network solids, conventional chemical bonds hold the chemical subunits together. The bonding between chemical subunits, however, is identical to that within the subunits, resulting in a continuous network of chemical bonds. One common examples of network solids are diamond (a form of pure carbon) Carbon exists as a pure element at room temperature in three different forms: graphite (the most stable form), diamond, and fullerene.
Diamonds
The structure of diamond is shown at the right in a "ball-and-stick" format. The balls represent the carbon atoms and the sticks represent a covalent bond. Be aware that in the "ball-and-stick" representation the size of the balls do not accurately represent the size of carbon atoms. In addition, a single stick is drawn to represent a covalent bond irrespective of whether the bond is a single, double, or triple bond or requires resonance structures to represent. In the diamond structure, all bonds are single covalent bonds (\(\sigma\) bonds). The "space-filling" format is an alternate representation that displays atoms as spheres with a radius equal to the van der Waals radius, thus providing a better sense of the size of the atoms.
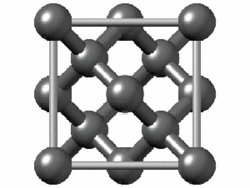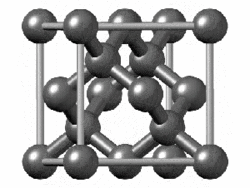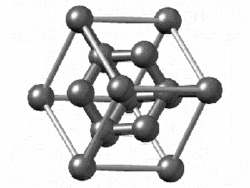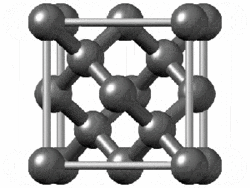
Notice that diamond is a network solid. The entire solid is an "endless" repetition of carbon atoms bonded to each other by covalent bonds. (In the display at the right, the structure is truncated to fit in the display area.)
Questions to consider:
- What is the bonding geometry around each carbon?
- What is the hybridization of carbon in diamond?
- The diamond structure consists of a repeating series of rings. How many carbon atoms are in a ring?
- Diamond are renowned for its hardness. Explain why this property is expected on the basis of the structure of diamond.
Graphite
The most stable form of carbon is graphite. Graphite consists of sheets of carbon atoms covalently bonded together. These sheets are then stacked to form graphite. Figure \(\PageIndex{3}\) shows a ball-and-stick representation of graphite with sheets that extended "indefinitely" in the xy plane, but the structure has been truncated for display purposed. Graphite may also be regarded as a network solid, even though there is no bonding in the z direction. Each layer, however, is an "endless" bonded network of carbon atoms.
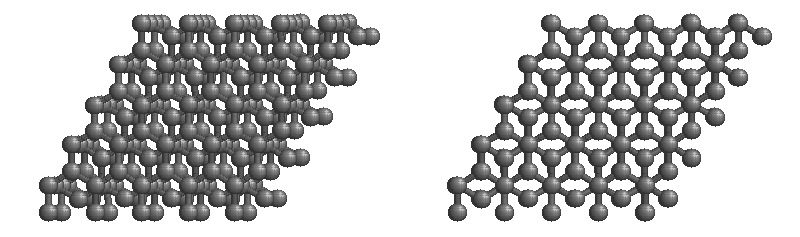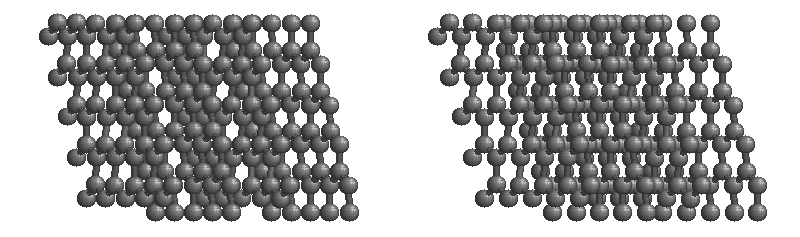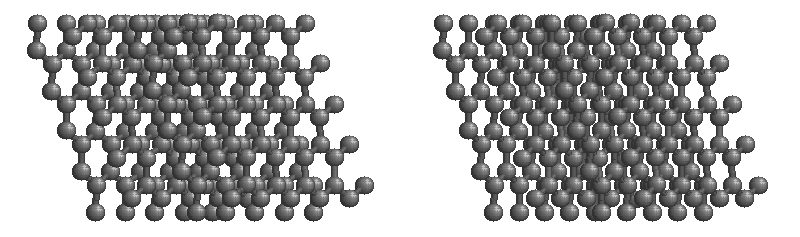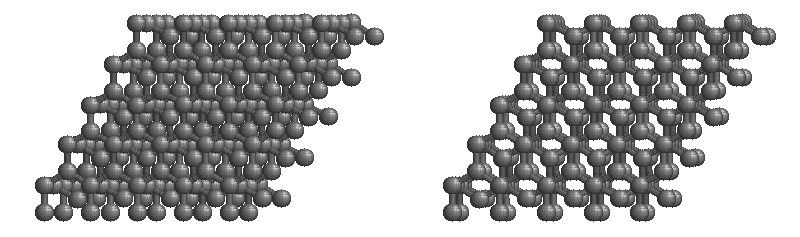
Questions to consider:
- What is the bonding geometry around each carbon?
- What is the hybridization of carbon in graphite?
- The a layer of the graphite structure consists of a repeating series of rings. How many carbon atoms are in a ring?
- What force holds the carbon sheets together in graphite?
- Graphite is very slippery and is often used in lubricants. Explain why this property is expected on the basis of the structure of graphite.
- The slipperiness of graphite is enhanced by the introduction of impurities. Where would such impurities be located and why would they make graphite a better lubricant?
Fullerenes
Until the mid 1980's, pure carbon was thought to exist in two forms: graphite and diamond. The discovery of C60 molecules in interstellar dust in 1985 added a third form to this list. The existence of C60, which resembles a soccer ball, had been hypothesized by theoretians for many years. In the late 1980's synthetic methods were developed for the synthesis of C60, and the ready availability of this form of carbon led to extensive research into its properties.
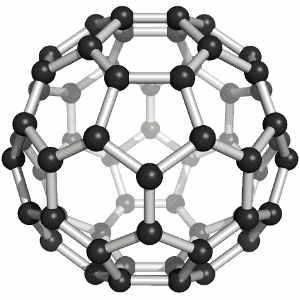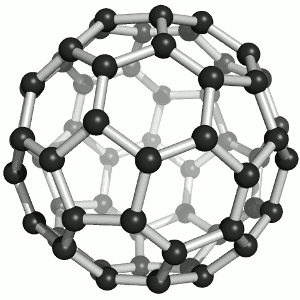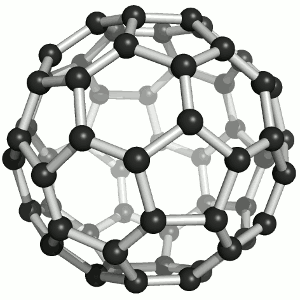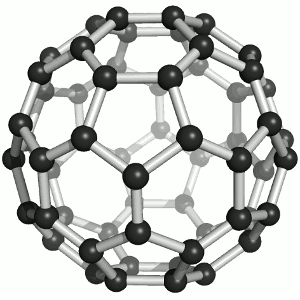
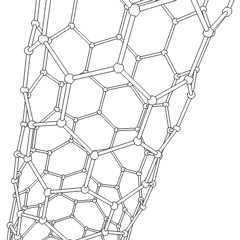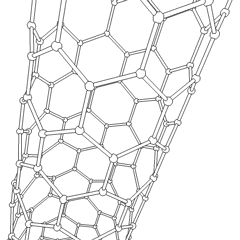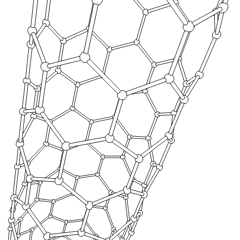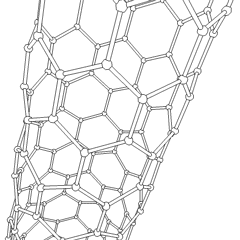
The C60 molecule (Figure \(\PageIndex{4}\); left), is called buckminsterfullerene, though the shorter name fullerene is often used. The name is a tribute to the American architect R. Buckminster Fuller, who is famous for designing and constructing geodesic domes which bear a close similarity to the structure of C60. As is evident from the display, C60 is a sphere composed of six-member and five-member carbon rings. These balls are sometimes fondly referred to as "Bucky balls". It should be noted that fullerenes are an entire class of pure carbon compounds rather than a single compound. A distorted sphere containing more than 60 carbon atoms have also been found, and it is also possible to create long tubes (Figure \(\PageIndex{4}\); right). All of these substances are pure carbon.
Questions to Consider
- What is the bonding geometry around each carbon? (Note that this geometry is distorted in \(C_{60}\).)
- What is the hybridization of carbon in fullerene?
- A single crystal of C60 falls into which class of crystalline solids?
- It has been hypothesized that C60 would make a good lubricant. Why might C60 make a good lubricant?
Metallic Solids
Metallic solids such as crystals of copper, aluminum, and iron are formed by metal atoms Figure \(\PageIndex{5}\). The structure of metallic crystals is often described as a uniform distribution of atomic nuclei within a “sea” of delocalized electrons. The atoms within such a metallic solid are held together by a unique force known as metallic bonding that gives rise to many useful and varied bulk properties. All exhibit high thermal and electrical conductivity, metallic luster, and malleability. Many are very hard and quite strong. Because of their malleability (the ability to deform under pressure or hammering), they do not shatter and, therefore, make useful construction materials.
Metals are characterized by their ability to reflect light, called luster, their high electrical and thermal conductivity, their high heat capacity, and their malleability and ductility. Every lattice point in a pure metallic element is occupied by an atom of the same metal. The packing efficiency in metallic crystals tends to be high, so the resulting metallic solids are dense, with each atom having as many as 12 nearest neighbors.

Bonding in metallic solids is quite different from the bonding in the other kinds of solids we have discussed. Because all the atoms are the same, there can be no ionic bonding, yet metals always contain too few electrons or valence orbitals to form covalent bonds with each of their neighbors. Instead, the valence electrons are delocalized throughout the crystal, providing a strong cohesive force that holds the metal atoms together.
Valence electrons in a metallic solid are delocalized, providing a strong cohesive force that holds the atoms together.
The strength of metallic bonds varies dramatically. For example, cesium melts at 28.4°C, and mercury is a liquid at room temperature, whereas tungsten melts at 3680°C. Metallic bonds tend to be weakest for elements that have nearly empty (as in Cs) or nearly full (Hg) valence subshells, and strongest for elements with approximately half-filled valence shells (as in W). As a result, the melting points of the metals increase to a maximum around group 6 and then decrease again from left to right across the d block. Other properties related to the strength of metallic bonds, such as enthalpies of fusion, boiling points, and hardness, have similar periodic trends.

A somewhat oversimplified way to describe the bonding in a metallic crystal is to depict the crystal as consisting of positively charged nuclei in an electron sea (Figure \(\PageIndex{6}\)). In this model, the valence electrons are not tightly bound to any one atom but are distributed uniformly throughout the structure. Very little energy is needed to remove electrons from a solid metal because they are not bound to a single nucleus. When an electrical potential is applied, the electrons can migrate through the solid toward the positive electrode, thus producing high electrical conductivity. The ease with which metals can be deformed under pressure is attributed to the ability of the metal ions to change positions within the electron sea without breaking any specific bonds. The transfer of energy through the solid by successive collisions between the metal ions also explains the high thermal conductivity of metals. This model does not, however, explain many of the other properties of metals, such as their metallic luster and the observed trends in bond strength as reflected in melting points or enthalpies of fusion. Some general properties of the four major classes of solids are summarized in Table \(\PageIndex{2}\).
| Ionic Solids | Molecular Solids | Covalent Solids | Metallic Solids |
|---|---|---|---|
| *Many exceptions exist. For example, graphite has a relatively high electrical conductivity within the carbon planes, and diamond has the highest thermal conductivity of any known substance. | |||
| poor conductors of heat and electricity | poor conductors of heat and electricity | poor conductors of heat and electricity* | good conductors of heat and electricity |
| relatively high melting point | low melting point | high melting point | melting points depend strongly on electron configuration |
| hard but brittle; shatter under stress | soft | very hard and brittle | easily deformed under stress; ductile and malleable |
| relatively dense | low density | low density | usually high density |
| dull surface | dull surface | dull surface | lustrous |
The general order of increasing strength of interactions in a solid is:
molecular solids < ionic solids ≈ metallic solids < covalent solids
Example \(\PageIndex{1}\)
Classify Ge, RbI, C6(CH3)6, and Zn as ionic, molecular, covalent, or metallic solids and arrange them in order of increasing melting points.
Given: compounds
Asked for: classification and order of melting points
Strategy:
- Locate the component element(s) in the periodic table. Based on their positions, predict whether each solid is ionic, molecular, covalent, or metallic.
- Arrange the solids in order of increasing melting points based on your classification, beginning with molecular solids.
Solution:
A Germanium lies in the p block just under Si, along the diagonal line of semimetallic elements, which suggests that elemental Ge is likely to have the same structure as Si (the diamond structure). Thus Ge is probably a covalent solid. RbI contains a metal from group 1 and a nonmetal from group 17, so it is an ionic solid containing Rb+ and I− ions. The compound C6(CH3)6 is a hydrocarbon (hexamethylbenzene), which consists of isolated molecules that stack to form a molecular solid with no covalent bonds between them. Zn is a d-block element, so it is a metallic solid.
B Arranging these substances in order of increasing melting points is straightforward, with one exception. We expect C6(CH3)6 to have the lowest melting point and Ge to have the highest melting point, with RbI somewhere in between. The melting points of metals, however, are difficult to predict based on the models presented thus far. Because Zn has a filled valence shell, it should not have a particularly high melting point, so a reasonable guess is C6(CH3)6 < Zn ~ RbI < Ge. The actual melting points are C6(CH3)6, 166°C; Zn, 419°C; RbI, 642°C; and Ge, 938°C. This agrees with our prediction.
Exercise \(\PageIndex{1}\)
Classify C60, BaBr2, GaAs, and AgZn as ionic, covalent, molecular, or metallic solids and then arrange them in order of increasing melting points.
Answer
C60 (molecular) < AgZn (metallic) ~ BaBr2 (ionic) < GaAs (covalent). The actual melting points are C60, about 300°C; AgZn, about 700°C; BaBr2, 856°C; and GaAs, 1238°C.
Summary
The major types of solids are ionic, molecular, covalent, and metallic. Ionic solids consist of positively and negatively charged ions held together by electrostatic forces; the strength of the bonding is reflected in the lattice energy. Ionic solids tend to have high melting points and are rather hard. Molecular solids are held together by relatively weak forces, such as dipole–dipole interactions, hydrogen bonds, and London dispersion forces. As a result, they tend to be rather soft and have low melting points, which depend on their molecular structure. Covalent solids consist of two- or three-dimensional networks of atoms held together by covalent bonds; they tend to be very hard and have high melting points. Metallic solids have unusual properties: in addition to having high thermal and electrical conductivity and being malleable and ductile, they exhibit luster, a shiny surface that reflects light. An alloy is a mixture of metals that has bulk metallic properties different from those of its constituent elements. Alloys can be formed by substituting one metal atom for another of similar size in the lattice (substitutional alloys), by inserting smaller atoms into holes in the metal lattice (interstitial alloys), or by a combination of both. Although the elemental composition of most alloys can vary over wide ranges, certain metals combine in only fixed proportions to form intermetallic compounds with unique properties.
Contributors and Attributions
Paul Flowers (University of North Carolina - Pembroke), Klaus Theopold (University of Delaware) and Richard Langley (Stephen F. Austin State University) with contributing authors. Textbook content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at http://cnx.org/contents/85abf193-2bd...a7ac8df6@9.110).

