5.4: Enthalpy of Reaction

Learning Objectives

• To understand how enthalpy pertains to chemical reactions

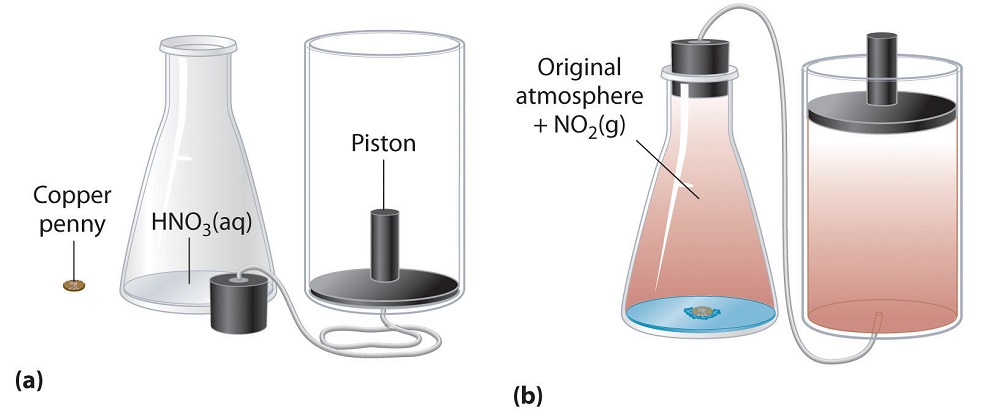
We have stated that the change in energy (ΔU) is equal to the sum of the heat produced and the work performed. Work done by an expanding gas is called pressure-volume work, (or just PV work). Consider, for example, a reaction that produces a gas, such as dissolving a piece of copper in concentrated nitric acid. The chemical equation for this reaction is as follows:

\[Cu_{(s)} + 4HNO_{3(aq)} \rightarrow Cu(NO_3)_{2(aq)} + 2H_2O_{(l)} + 2NO_{2(g)} \label{5.4.1}\]

If the reaction is carried out in a closed system that is maintained at constant pressure by a movable piston, the piston will rise as nitrogen dioxide gas is formed (Figure (\PageIndex{1}\)). The system is performing work by lifting the piston against the downward force exerted by the atmosphere (i.e., atmospheric pressure). We find the amount of PV work done by multiplying the external pressure P by the change in volume caused by movement of the piston (ΔV). At a constant external pressure (here, atmospheric pressure)

\[w = −PΔV \label{5.4.2}\]

The negative sign associated with PV work done indicates that the system loses energy when the volume increases. If the volume increases at constant pressure (ΔV > 0), the work done by the system is negative, indicating that a system has lost energy by performing work on its surroundings. Conversely, if the volume decreases (ΔV < 0), the work done by the system is positive, which means that the surroundings have performed work on the system, thereby increasing its energy.

Figure \(\PageIndex{1}\): An Example of Work Performed by a Reaction Carried Out at Constant Pressure. (a) Initially, the system (a copper penny and concentrated nitric acid) is at atmospheric pressure. (b) When the penny is added to the nitric acid, the volume of NO₂ gas that is formed causes the piston to move upward to maintain the system at atmospheric pressure. In doing so, the system is performing work on its surroundings.

The internal energy \(U\) of a system is the sum of the kinetic energy and potential energy of all its components. It is the change in internal energy that produces heat plus work. To measure the energy changes that occur in chemical reactions, chemists usually use a related thermodynamic quantity called enthalpy (H) (from the Greek enthalpein, meaning “to warm”). The enthalpy of a system is defined as the sum of its internal energy \(U\) plus the product of its pressure P and volume V:

\[H =U + PV \label{5.4.3}\]

Because internal energy, pressure, and volume are all state functions, enthalpy is also a state function.

If a chemical change occurs at constant pressure (i.e., for a given P, ΔP = 0), the change in enthalpy (ΔH) is

\[ ΔH = Δ(U + PV) = ΔU + ΔPV = ΔU + PΔV \label{5.4.4}\]

Substituting q + w for ΔU (Equation \(\ref{5.4.4}\)) and −w for PΔV (Equation \(\ref{5.4.2}\)), we obtain

\[ΔH = ΔU + PΔV = q_p + w − w = q_p \label{5.4.5}\]

The subscript \(p\) is used here to emphasize that this equation is true only for a process that occurs at constant pressure. From Equation \(\ref{5.4.5}\) we see that at constant pressure the change in enthalpy, ΔH of the system, defined as H_final − H_initial, is equal to the heat gained or lost.

\[ΔH = H_{final} − H_{initial} = q_p \label{5.4.6}\]

Just as with ΔU, because enthalpy is a state function, the magnitude of ΔH depends on only the initial and final states of the system, not on the path taken. Most important, the enthalpy change is the same even if the process does not occur at constant pressure.

To find \(ΔH\) for a reaction, measure \(q_p\).

When we study energy changes in chemical reactions, the most important quantity is usually the enthalpy of reaction (ΔH_rxn), the change in enthalpy that occurs during a reaction (such as the dissolution of a piece of copper in nitric acid). If heat flows from a system to its surroundings, the enthalpy of the system decreases, so ΔH_rxn is negative. Conversely, if heat flows from the surroundings to a system, the enthalpy of the system increases, so ΔH_rxn is positive. Thus ΔH_rxn < 0 for an exothermic reaction, and ΔH_rxn > 0 for an endothermic reaction. In chemical reactions, bond breaking requires an input of energy and is therefore an endothermic process, whereas bond making releases energy, which is an exothermic process. The sign conventions for heat flow and enthalpy changes are summarized in the following table:

Reaction Type	q	ΔHrxn
exothermic	< 0	< 0 (heat flows from a system to its surroundings)
endothermic	> 0	> 0 (heat flows from the surroundings to a system)

If ΔH_rxn is negative, then the enthalpy of the products is less than the enthalpy of the reactants; that is, an exothermic reaction is energetically downhill (part (a) in Figure 5.4.2). Conversely, if ΔH_rxn is positive, then the enthalpy of the products is greater than the enthalpy of the reactants; thus, an endothermic reaction is energetically uphill (part (b) in Figure \(\PageIndex{2}\)). Two important characteristics of enthalpy and changes in enthalpy are summarized in the following discussion.

Bond breaking ALWAYS requires an input of energy; bond making ALWAYS releases energy.y.

Figure \(\PageIndex{2}\): The Enthalpy of Reaction. Energy changes in chemical reactions are usually measured as changes in enthalpy. (a) If heat flows from a system to its surroundings, the enthalpy of the system decreases, ΔH_rxn is negative, and the reaction is exothermic; it is energetically downhill. (b) Conversely, if heat flows from the surroundings to a system, the enthalpy of the system increases, ΔH_rxn is positive, and the reaction is endothermic; it is energetically uphill.

• Reversing a reaction or a process changes the sign of ΔH. Ice absorbs heat when it melts (electrostatic interactions are broken), so liquid water must release heat when it freezes (electrostatic interactions are formed):

  \( \begin{matrix}
  heat+ H_{2}O(s) \rightarrow H_{2}O(l) & \Delta H > 0
  \end{matrix} \label{5.4.7} \)

  \( \begin{matrix}
  H_{2}O(l) \rightarrow H_{2}O(s) + heat & \Delta H < 0
  \end{matrix} \label{5.4.8} \)

  In both cases, the magnitude of the enthalpy change is the same; only the sign is different.

• Enthalpy is an extensive property (like mass). The magnitude of ΔH for a reaction is proportional to the amounts of the substances that react. For example, a large fire produces more heat than a single match, even though the chemical reaction—the combustion of wood—is the same in both cases. For this reason, the enthalpy change for a reaction is usually given in kilojoules per mole of a particular reactant or product. Consider Equation \(\ref{5.4.9}\), which describes the reaction of aluminum with iron(III) oxide (Fe₂O₃) at constant pressure. According to the reaction stoichiometry, 2 mol of Fe, 1 mol of Al₂O₃, and 851.5 kJ of heat are produced for every 2 mol of Al and 1 mol of Fe₂O₃ consumed:

  \[ 2Al\left (s \right )+Fe_{2}O_{3}\left (s \right ) \rightarrow 2Fe\left (s \right )+Al_{2}O_{3}\left (s \right )+ 815.5 \; kJ \label{5.4.9} \]

  Thus ΔH = −851.5 kJ/mol of Fe₂O₃. We can also describe ΔH for the reaction as −425.8 kJ/mol of Al: because 2 mol of Al are consumed in the balanced chemical equation, we divide −851.5 kJ by 2. When a value for ΔH, in kilojoules rather than kilojoules per mole, is written after the reaction, as in Equation \(\ref{5.4.10}\), it is the value of ΔH corresponding to the reaction of the molar quantities of reactants as given in the balanced chemical equation:

  \[ 2Al\left (s \right )+Fe_{2}O_{3}\left (s \right ) \rightarrow 2Fe\left (s \right )+Al_{2}O_{3}\left (s \right ) \;\;\;\; \Delta H_{rxn}= - 851.5 \; kJ \label{5.4.10} \]

  If 4 mol of Al and 2 mol of Fe₂O₃ react, the change in enthalpy is 2 × (−851.5 kJ) = −1703 kJ. We can summarize the relationship between the amount of each substance and the enthalpy change for this reaction as follows:

  \[ - \dfrac{851.5 \; kJ}{2 \; mol \;Al} = - \dfrac{425.8 \; kJ}{1 \; mol \;Al} = - \dfrac{1703 \; kJ}{4 \; mol \; Al} \label{5.4.6a} \]

The relationship between the magnitude of the enthalpy change and the mass of reactants is illustrated in Example \(\PageIndex{1}\).

Example \(\PageIndex{1}\): Melting Icebergs

Certain parts of the world, such as southern California and Saudi Arabia, are short of freshwater for drinking. One possible solution to the problem is to tow icebergs from Antarctica and then melt them as needed. If ΔH is 6.01 kJ/mol for the reaction at 0°C and constant pressure:

\[H_2O_{(s)} → H_2O_{(l)}\]

How much energy would be required to melt a moderately large iceberg with a mass of 1.00 million metric tons (1.00 × 10⁶ metric tons)? (A metric ton is 1000 kg.)

Given: energy per mole of ice and mass of iceberg

Asked for: energy required to melt iceberg

Strategy:

1. Calculate the number of moles of ice contained in 1 million metric tons (1.00 × 10⁶ metric tons) of ice.
2. Calculate the energy needed to melt the ice by multiplying the number of moles of ice in the iceberg by the amount of energy required to melt 1 mol of ice.

Solution:

A Because enthalpy is an extensive property, the amount of energy required to melt ice depends on the amount of ice present. We are given ΔH for the process—that is, the amount of energy needed to melt 1 mol (or 18.015 g) of ice—so we need to calculate the number of moles of ice in the iceberg and multiply that number by ΔH (+6.01 kJ/mol):

\[ \begin{matrix}
moles \; H_{2}O & = & 1.00\times 10^{6} \; metric \; tons H_{2}O \left ( \dfrac{1000 \; \cancel{kg}}{1 \; \cancel{metric \; ton}} \right ) \left ( \dfrac{1000 \; \cancel{g}}{1 \; \cancel{kg}} \right ) \left ( \dfrac{1 \; mol \; H_{2}O}{18.015 \; \cancel{g \; H_{2}O}} \right )\\
& = & 5.55\times 10^{10} \; mol H_{2}O
\end{matrix} \]

B The energy needed to melt the iceberg is thus

\[ \left ( \dfrac{6.01 \; kJ}{\cancel{mol \; H_{2}O}} \right )\left ( 5.55 \times 10^{10} \; \cancel{mol \; H_{2}O} \right )= 3.34 \times 10^{11} \; kJ \]

Because so much energy is needed to melt the iceberg, this plan would require a relatively inexpensive source of energy to be practical. To give you some idea of the scale of such an operation, the amounts of different energy sources equivalent to the amount of energy needed to melt the iceberg are shown in the table below.

Possible sources of the approximately 3.34 × 10¹¹ kJ needed to melt a 1.00 × 10⁶ metric ton iceberg

• Combustion of 3.8 × 10³ ft³ of natural gas
• Combustion of 68,000 barrels of oil
• Combustion of 15,000 tons of coal
• 1.1 × 10⁸ kilowatt-hours of electricity

Exercise \(\PageIndex{1}\): Thermite Reaction

If 17.3 g of powdered aluminum are allowed to react with excess Fe₂O₃, how much heat is produced?

Answer:

273 kJ

Enthalpies of Reaction

One way to report the heat absorbed or released would be to compile a massive set of reference tables that list the enthalpy changes for all possible chemical reactions, which would require an incredible amount of effort. Fortunately, Hess’s law allows us to calculate the enthalpy change for virtually any conceivable chemical reaction using a relatively small set of tabulated data, such as the following:

• Enthalpy of combustion (ΔH_comb) The change in enthalpy that occurs during a combustion reaction. Enthalpy changes have been measured for the combustion of virtually any substance that will burn in oxygen; these values are usually reported as the enthalpy of combustion per mole of substance.
• Enthalpy of fusion (ΔH_fus) The enthalpy change that acompanies the melting (fusion) of 1 mol of a substance. The enthalpy change that accompanies the melting, or fusion, of 1 mol of a substance; these values have been measured for almost all the elements and for most simple compounds.
• Enthalpy of vaporization (ΔH_vap) The enthalpy change that accompanies the vaporization of 1 mol of a substance. The enthalpy change that accompanies the vaporization of 1 mol of a substance; these values have also been measured for nearly all the elements and for most volatile compounds.
• Enthalpy of solution (ΔH_soln) The change in enthalpy that occurs when a specified amount of solute dissolves in a given quantity of solvent. The enthalpy change when a specified amount of solute dissolves in a given quantity of solvent.

Table \(\PageIndex{1}\): Enthalpies of Vaporization and Fusion for Selected Substances at Their Boiling Points and Melting Points

Substance	ΔHvap (kJ/mol)	ΔHfus (kJ/mol)
argon (Ar)	6.3	1.3
methane (CH4)	9.2	0.84
ethanol (CH3CH2OH)	39.3	7.6
benzene (C6H6)	31.0	10.9
water (H2O)	40.7	6.0
mercury (Hg)	59.0	2.29
iron (Fe)	340	14

The sign convention is the same for all enthalpy changes: negative if heat is released by the system and positive if heat is absorbed by the system.

Summary

For a chemical reaction, the enthalpy of reaction (\(ΔH_{rxn}\)) is the difference in enthalpy between products and reactants; the units of \(ΔH_{rxn}\) are kilojoules per mole. Reversing a chemical reaction reverses the sign of \(ΔH_{rxn}\).

Contributors and Attributions

• Modified by Joshua Halpern (Howard University)