8.3: Hartree-Fock Equations are Solved by the Self-Consistent Field Method
- Last updated
- Save as PDF
- Page ID
- 92402
Learning Objectives
- Show how the Hartree approximation can be used to solve for the wavefunctions and energies of multi-electron atoms.
- Understand the orbital approach of independent orbitals is an approximation to a mutlti-electron system with the motions of all electrons coupled together.
- Demonstate how the Self-Consistant Field (SCF) calculation is needed to support the Hartree approximation
The Hartree method is used to approximate the wavefunction and the energy of a quantum multi-electron system in a stationary state. This approximation assumes that the exact \(N\)-body wavefunction of the system can be approximated by a product of single-electron wavefunctions. By invoking the variational method, one can derive a set of \(N\)-coupled equations for the N spin orbitals. A solution of these equations yields the Hartree wavefunction and energy of the system. It is one step better than the "Ignorance is Bliss" approach, discussed previously, but still far from modern state-off-the-art methods.
Unsolvable Systems
The Hamiltonian for a generic multielectron atom includes nucleus-electron attraction terms for the additional electrons with a general charge \(Z\); e.g.
\[V_{\text{nuclear-electron}}(r_1) = -\dfrac {Z}{\left\vert\mathbf{r} - \mathbf{R}\right\vert} \label{8.3.1} \]
in atomic units with \(\left\vert\mathbf{r} - \mathbf{R}\right\vert\) is the distance between the electron and the nucleus, The Hamiltonian must also have terms for electron-electron repulsion (also in atomic units)
\[V_{\text{electron-electron}}(r_{12}) = \dfrac {1}{\left\vert \mathbf{r} - \mathbf{r}^{\prime} \right\vert} \nonumber \]
with \(\left\vert \mathbf{r} - \mathbf{r}^{\prime} \right\vert\) is the distance between electron 1 and electron 2. So the proper multi-electron Hamiltonian can be constructed
\[\hat {H} (r_1, r_2, ... r_n) = -\dfrac {\hbar ^2}{2m_e} \sum _i \nabla ^2_i + \sum _i V_{\text{nuclear-electron}} (r_i) + \sum _{i \ne j} V_{\text{electron-electron}} (r_{ij}) \label{8.3.3} \]
Given what we have learned from the previous quantum mechanical systems we’ve studied, we predict that exact solutions to the multi-electron Schrödinger equation would consist of a family of multi-electron wavefunctions, each with an associated energy eigenvalue. These wavefunctions and energies would describe the ground and excited states of the multi-electron atom, just as the hydrogen wavefunctions and their associated energies describe the ground and excited states of the hydrogen atom. We would predict quantum numbers to be involved, as well.
The fact that electrons interact through their electron-electron repulsion (final term in Equation \(\ref{8.3.3}\)) means that an exact wavefunction for a multi-electron system would be a single function that depends simultaneously upon the coordinates of all the electrons; i.e., a multi-electron wavefunction:
\[|\psi (r_1, r_2, \cdots r_i) \rangle \label{8.3.4} \]
Unfortunately, the electron-electron repulsion terms make it impossible to find an exact solution to the Schrödinger equation for many-electron atoms.
The Hartree Approximation
The method for finding best possible one-electron wavefunctions that was published by Douglas Hartree in 1948 and improved two years later by Vladimir Fock. For the Schrödinger equation to be analytically solvable, the variables must be separable - the variables are the coordinates of the electrons. To separate the variables in a way that retains information about electron-electron interactions, the electron-electron term (Equation \(\ref{8.3.1}\)) must be approximated so it depends only on the coordinates of one electron. Such an approximate Hamiltonian can account for the interaction of the electrons in an average way. The exact one-electron eigenfunctions of this approximate Hamiltonian then can be found by solving the Schrödinger equation. These functions are the best possible one-electron functions.
The Hartree approximation starts by invoking an initial ansatz that the multi-electron wavefunction in Equation \(\ref{8.3.4}\) can be expanded as a product of single-electron wavefunctions (i.e., orbitals)
\[ | \psi(\mathbf{r}_1,\mathbf{r}_2, \ldots, \mathbf{r}_N) \rangle \approx \psi_{1}(\mathbf{r}_1)\psi_{2}(\mathbf{r}_2) \ldots \psi_{N}(\mathbf{r}_N) \nonumber \]
from which it follows that the electrons are independent, and interact only via the mean-field Coulomb potential. This yields one-electron Schrödinger equations of the form
\[-\dfrac{\hbar^{2}}{2m} \nabla^{2}\psi_{i}(\mathbf{r}) + V(\mathbf{r})\psi_{i}(\mathbf{r}) = \epsilon_{i}\psi_{i}(\mathbf{r}) \nonumber \]
or
\[H_e(r) \psi_{i}(\mathbf{r}) = \epsilon_{i}\psi_{i}(\mathbf{r}) \nonumber \]
where \(V(r)\) is the potential in which the electron moves; this includes both the nuclear-electron interaction
\[V_{nucleus}(\mathbf{r}) = -Ze^{2}\sum_{R} \dfrac{1}{\left\vert\mathbf{r} - \mathbf{R}\right\vert} \nonumber \]
and the mean field arising from the \(N-1\) other electrons. We smear the other electrons out into a smooth negative charge density \(\rho(\mathbf{r}')\) leading to a potential of the form
\[V_{electron}(\mathbf{r}) = -e\int d\mathbf{r}^{\prime} \rho(\mathbf{r}^{\prime}) \dfrac{1}{\left\vert \mathbf{r} - \mathbf{r}^{\prime} \right\vert} \nonumber \]
where
\[\rho(\mathbf{r}) = \sum_{i}^{\text{occupied}}\vert\psi(\mathbf{r})\vert^{2}. \nonumber \]
The sum over runs over all occupied states; i.e., only the states of electrons that exist in the atom. The wavefunctions that from this approach with the Hamiltonian \(H_e(r)\) involve possess three kinds of energies discussed below.
Three Energies within the Hartree Approximation
The total energy \(\epsilon_j\) of the orbital \(\phi_j\), is the sum of the above three contributions:
- Kinetic Energy: The Kinetic energy of the electron has an average value is computed by taking the expectation value of the kinetic energy operator \[\dfrac{- \hbar^2}{2m} \nabla^2 \nonumber \] with respect to any particular solution \(\phi_j(r)\) to the Schrödinger equation: \[KE = \langle\phi_j| \dfrac{- \hbar^2}{2m} \nabla^2 |\phi_j\rangle \nonumber \]
- Nuclear-Electron Coulombic Attraction Energy: Coulombic attraction energy with the nucleus of charge \(Z\): \[\langle\phi_j| \dfrac{-Z e^2}{\left\vert\mathbf{r} - \mathbf{R}\right\vert} |\phi_j\rangle \nonumber \]
- Electron-Electron Coulombic Repulsion Energy: Coulomb repulsion energies with all of the \(N-1\) other electrons, which are assumed to occupy other atomic orbitals denoted \(\phi_K\), with this energy computed as \[\sum_{j\neq k} \langle\phi_j(r) \phi_k(r’) |\dfrac{e^2}{|r-r’|} | \phi_j(r) \phi_k(r’)\rangle.\label{8.3.8} \] The Dirac notation \(\langle\phi_j(r) \phi_k(r’) |\dfrac{e^2}{|r-r’|} | \phi_j(r) \phi_k(r’)\rangle\) is used to represent the two-electron (six-dimensional) Coulomb integral \[J_{j,k} = \int |\phi_j(r)|^2 |\phi_k(r’)|^2 \dfrac{e^2}{r-r'} dr dr’ \nonumber \] that describes the Coulomb repulsion between the charge density \(|\phi_j(r)|^2\) for the electron in \(\phi_j\) and the charge density \(|\phi_k(r’)|^2\) for the electron in \(\phi_k\). Of course, the sum over \(k\) must be limited to exclude \(k=j\) to avoid counting a “self-interaction” of the electron in orbital \(\phi_j\) with itself.
Adding these all together to get the total energy \(\epsilon_j\) of the orbital \(\phi_j\):
\[\epsilon_J = \langle\phi_j| \dfrac{- \hbar^2}{2m} \nabla^2 |\phi_j\rangle + \langle\phi_j| \dfrac{-Z e^2}{\left\vert\mathbf{r} - \mathbf{R}\right\vert} |\phi_j\rangle + \sum_{j\neq k} \langle\phi_j(r) \phi_k(r’) |\dfrac{e^2}{|r-r’|} | \phi_j(r) \phi_k(r’)\rangle. \nonumber \]
This treatment of the electrons and their orbitals is referred to as the Hartree-level of theory.
When screened hydrogenic atomic orbitals are used to approximate the \(\phi_j\) and \(\phi_K\) orbitals, the resultant \(\epsilon_J\) values do not produce accurate predictions. For example, the negative of \(\epsilon_J\) should approximate the ionization energy for removal of an electron from the orbitals \(\phi_j\). Such ionization potentials (IP s) can be measured, and the measured values do not agree well with the theoretical values when a crude screening approximation is made for the atomic orbitals.
The Self-Consistant Field (SCF) Approach to the Variational Method
The Hartree Equations are nonlinear and must be solved iteratively. This is because if particles interact, that interaction must be in the Hamiltonian. So until we know where the particles are, we cannot write down the Hamiltonian, but until we know the Hamiltonian, we cannot tell where the particles are.
The idea is to solve the Schrödinger equation for an electron moving in the potential of the nucleus and all the other electrons. We start with a guess for the trial electron charge density, solve N/2 one-particle Schrödinger equations (initially identical) to obtain N electron wavefunctions. Then we construct the potential for each wavefunction from that of the nucleus and that of all the other electrons, symmetrize it, and solve the N/2 Schrödinger equations again. This method is ideal for a computer, because it is easily written as an algorithm (Figure 8.3.1 ).
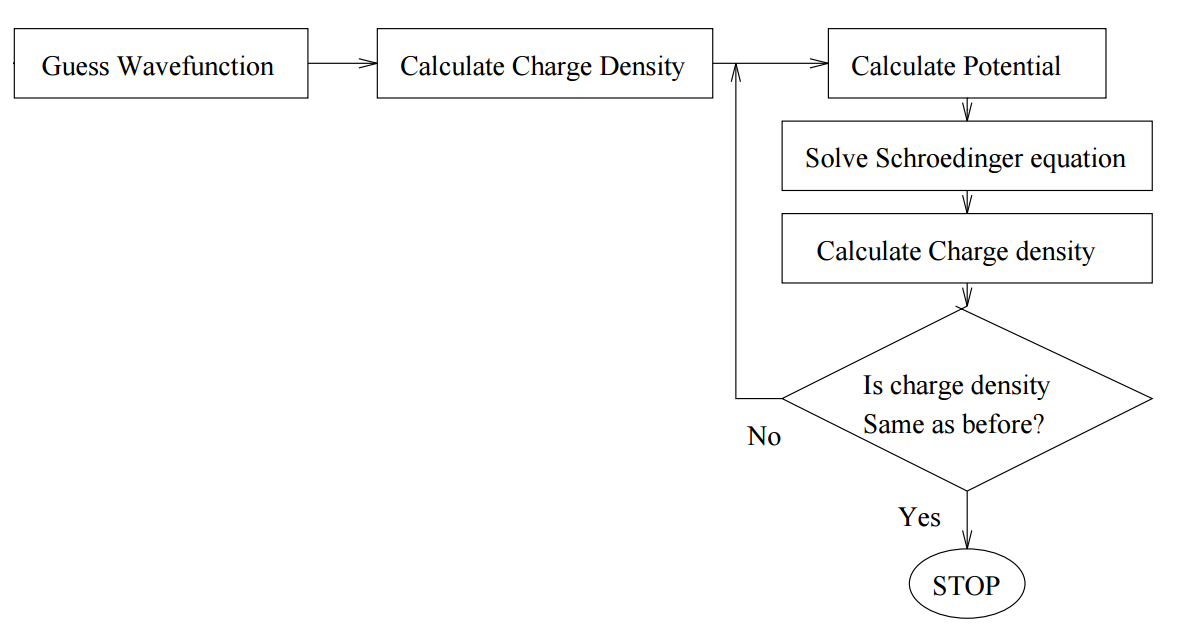
Although we are concerned here with atoms, the same methodology is used for molecules or even solids (with appropriate potential symmetries and boundary conditions). This is a variational method, so wherever we refer to wavefunctions, we assume that they are expanded in some appropriate basis set.
Fock improved on Hartree’s method by using proper "antisymmetrized wavefunctions" (called the Hartree-Fock method) instead of simple one-electron wavefunctions.
Shielding and Effective Charges Concepts are Useful
The hydrogen-like orbitals provide qualitative descriptions of orbitals of atoms with more than a single electron. By introducing the concept of screening as a way to represent the repulsive interactions among the electrons of an atom, an effective nuclear charge \(Z_{\rm eff}\) can be used in place of \(Z\) in the hydrogenic \(\psi_{n,l,m}\) and \(E_{n,l}\) formulas to generate approximate atomic orbitals to be filled by electrons in a many-electron atom. For example, in the crudest approximation of a carbon atom, the two \(1s\) electrons experience the full nuclear attraction so \(Z_{\rm eff} =6\) for them, whereas the \(2s\) and \(2p\) electrons are screened by the two \(1s\) electrons, so \(Z_{\rm eff}= 4\) for them. Within this approximation, one then occupies two \(1s\) orbitals with \(Z=6\), two \(2s\) orbitals with \(Z=4\) and two \(2p\) orbitals with \(Z=4\) in forming the full six-electron product wavefunction of the lowest-energy state of carbon
\[ | \psi(1, 2, …, 6) \rangle = | \psi_{1s}(1) \psi_{1s}(2) \psi_{2s}(3) \ldots \psi_{1p}(6) \rangle . \label{8.3.6} \]
However, such approximate orbitals are not sufficiently accurate to be of use in quantitative simulations of atomic and molecular structure. In particular, their energies do not properly follow the trends in atomic orbital (AO) energies that are taught in introductory chemistry classes (Figure 8.3.2 ).
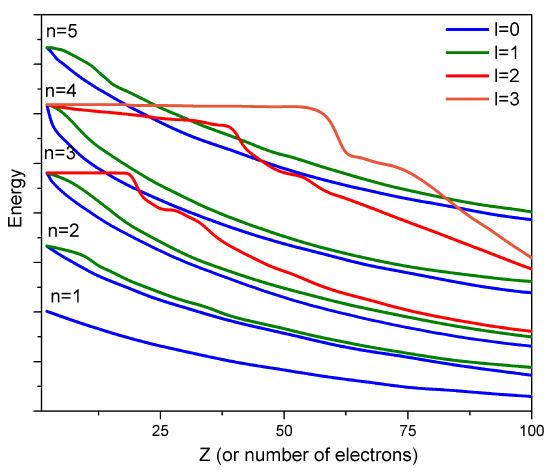
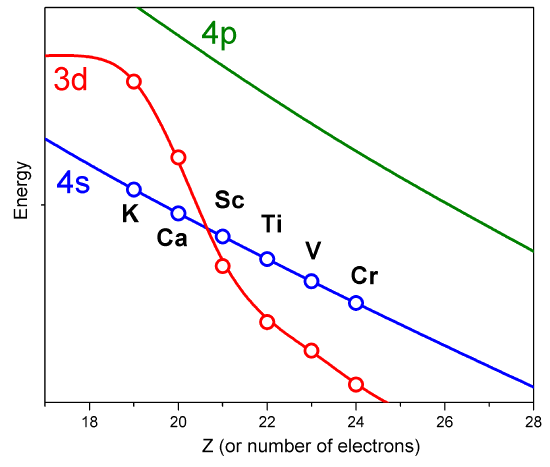
For example, the relative energies of the \(3d\) and \(4s\) orbitals are not adequately described in a model that treats electron repulsion effects in terms of a simple screening factor. So, now it is time to examine how we can move beyond the screening model and take the electron repulsion effects, which cause the inter-electronic couplings that render the Schrödinger equation insolvable, into account in a more reliable manner.

