3.4: The Quantum Mechanical Free Particle
- Page ID
- 93251
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- To desribe the quantum mechanical free particle
- To recognize the application of the heisenburg uncertainty principle applied to the free particle
- To identify the lack of quantization of the free particle and understand why.
The simplest system in quantum mechanics has the potential energy \(V=0\) everywhere. This is called a free particle since it has no forces acting on it. We consider the one-dimensional case, with motion only in the \(x\)-direction, giving the time-independent Schrödinger equation
\[- \dfrac{\hbar^{2}}{2m}\dfrac{d^{2}\psi (x)}{dx^2}= E\psi (x)\label{1}\]
or more simply
\[ \hat{H} \psi (x)= E\psi (x)\label{H1}\]
with
\[ \hat{H} = - \dfrac{\hbar^{2}}{2m}\dfrac{d^{2} }{dx^2} \label{H2}\]
Total derivatives can be used since there is one independent variable. The equation simplifies to
\[\psi'' (x)+k^{2}\psi (x)=0\label{2}\]
with the definition
\[k^2 \equiv \dfrac{2mE}{\hbar^2}\label{3}\]
Possible solutions of Equation \ref{2} are
\[\psi (x)= const\begin{Bmatrix}
\sin(kx)\\
\cos(kx)\\
e^{\pm ikx}\end{Bmatrix}\label{4}\]
There is no restriction on the value of \(k\). Thus a free particle, even in quantum mechanics, can have any non-negative value of the energy
\[E=\dfrac{\hbar^2k^2}{2m}\geq 0\label{5}\]
The energy levels in this case are not quantized and correspond to the same continuum of kinetic energy shown by a classical particle.
Consider for a free particle (i.e., \(V(x)=0\)) moving in one dimension.
- Demonstrate that \(\sin (kx)\), \(\cos (kx)\), and \(e^{\pm ikx}\) are indeed eigenfunctions of \(\hat{H}\).
- What are their corresponding eigenstates?
- What are the energies not quantized?
- Approach
-
To demonstrate that a function is indeed a specific eigenfunction \(f(x)\) of an operator \(\hat{O}\), we have to ask if this Eigenvalue equation is correct, i.e., \[ \hat{O} f(x) = \lambda f(x) \label{Eigen1}\] where \(\lambda\) is the eigenvalue associated with that eigenfunction associated with the operator. Change the operator and the eigenfunctions and eigenvalues will change. Change the eigenfunction and the eigenvalue will change. They are all connected like the Mufasa's "Circle of Life."
- Solution a
-
Let's take the \(\sin (kx)\) function and the Hamiltonian operator (Equation \ref{H2}) and insert it into Equation \ref{Eigen1} and is if the equality is ensured. Keep in mind that any value of \(lambda\) will work as long as it is a constant.
\[ - \dfrac{\hbar^{2}}{2m}\dfrac{d^{2}}{dx^2} \sin (kx) \overset{?}{=} \lambda \sin (kx) \label{Eigen1A}\]
first step in evaluating the 2nd derivative
\[ - \dfrac{\hbar^{2}}{2m} k \dfrac{d }{dx} (\cos (kx)) \overset{?}{=} \lambda \sin (kx) \label{Eigen1B}\]
and second step
\[ + \dfrac{\hbar^{2}}{2m} k^2 (\sin (kx)) \overset{?}{=} \lambda \sin (kx) \label{Eigen1C}\]
This equation is confirmed when
\[\lambda = + \dfrac{\hbar^{2} k^2}{2m} \]
Which makes sense when compared to Equation \ref{5} since the Hamiltonian gives the total energy \(E\).
- Solution b
-
As shown in the Solution a, the Eigenvalue equation is confirm to be correct for all \(\sin (kx)\) functions (so they are eigenfunctions of the Hamiltonian) and the eigenvalues are \[\lambda = + \dfrac{\hbar^{2} k^2}{2m} .\] Eigenvalues can be positive, negative, real, imaginary and complex and all of the above.
- Solution c
-
Since any value of \(k\) is allowed in the \(\sin (kx)\) eigenfunctions (i.e., the Eigenvalue equation holds for all values of \(k\)), then there is no quantization. We need boundary conditions to force the quantization like with the Bohr hydrogen atom.
Consider for a free particle (i.e., \(V(x)=0\)) moving in one dimension.
- Demonstrate that \(\cos (kx)\) and \(e^{\pm ikx}\) are eigenfunctions of \(\hat{H}\).
- What are their corresponding eigenstates?
- Is momentum quantized for a free particle?
It is of interest also to consider the x-component of linear momentum for the free-particle solutions (Equation \ref{4}). The eigenvalue equation for momentum is
\[\hat{p}_{x}\psi (x)=-i\hbar\dfrac{d\psi (x)}{dx}=p\psi (x)\label{6}\]
where we have denoted the momentum eigenvalue as \(p\).
It is easily shown that neither of the functions \(\sin kx\) or \(\cos kx\) from Equation \ref{4} is an eigenfunction of \( \hat{p}_{x}\). However, \(e^{\pm ikx}\) are both eigenfunctions with eigenvalues \(p=\pm\hbar k\), respectively. Evidently the momentum \(p\) can take on any real value between -\(\infty\) and +\(\infty\). The kinetic energy, equal to \(E=p^2/2m\), can correspondingly have any value between 0 and +\(\infty\).
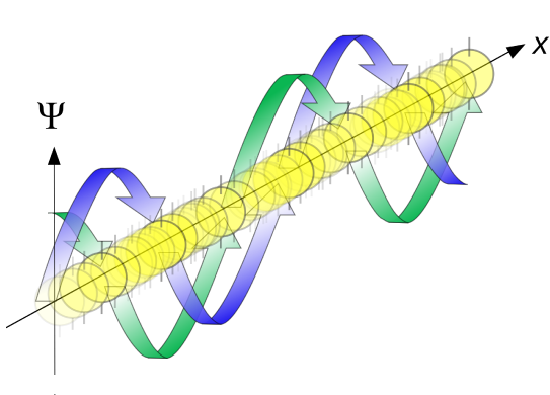
A free particle, even in quantum mechanics, can have any non-negative value of the energy
Consider for a free particle (i.e., \(V(x)=0\)) moving in one dimension.
- Demonstrate that \(e^{\pm ikx}\) are eigenfunctions of \(\hat{p}_{x}\).
- What are their corresponding eigenstates?
Show that neither \(\sin kx\) nor \(\cos kx\) are eigenstates of \(\hat{p}_{x}\) for a free particle (i.e., \(V(x)=0\)) moving in one dimension.
Superpositions
The functions \(\sin kx\) and \(\cos kx\), while not eigenfunctions of \(\hat{p}_{x}\), are each superpositions of the two eigenfunctions \(e^{\pm ikx}\), by virtue of the trigonometric identities
\[\cos (kx)=\dfrac{1}{2}(e^{ikx} +e^{-ikx})\]
and
\[\sin(kx)= \dfrac{1}{2i}(e^{ikx} -e^{-ikx})\label{7}\]
The eigenfunction \(e^{ikx}\) for \( k > 0\) represents the particle moving from left to right on the x-axis (blue curve in Figure \(\PageIndex{2}\)) with momentum \(p > 0\). Correspondingly, \(e^{-ikx}\) represents motion from right to left with \(p < 0\) (red curve in Figure \(\PageIndex{2}\)).
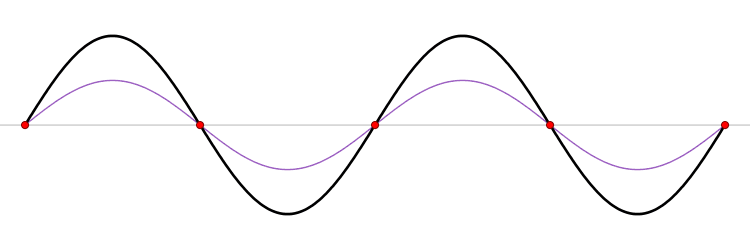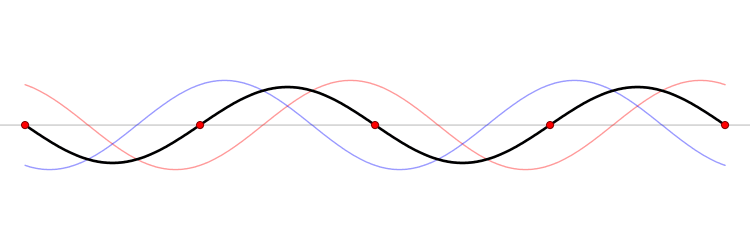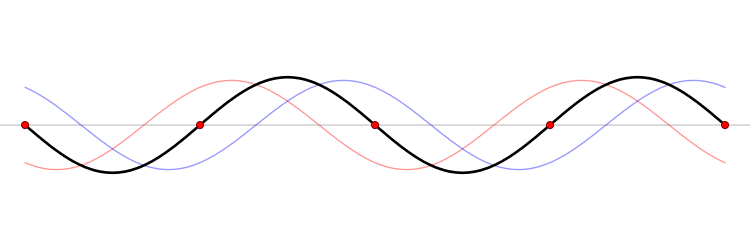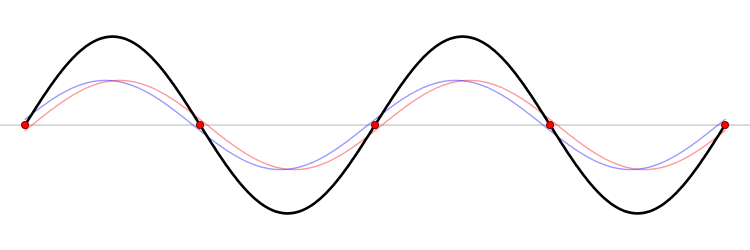
The functions \(\sin (kx)\) and \(\cos (kx\)) represent standing waves, obtained by superposition of opposing complex waves. Although these two trigonometry functions are not eigenfunctions of \(\hat{p}_{x}\), they are eigenfunctions of \(\hat{p}^2_{x}\) and hence they are eigenfunctions of the Hamiltonian operator \(\hat{H}\).
It is important to note that while \(\sin kx\) nor \(\cos kx\) are not eigenstates of momentum, these functions can be decomposed into a combination of functions that are eigenstates (Equation \ref{6} and \ref{7}). The ability to decompose wavefunctions into (linear) combinations of eigenstates is used throughout quantum mechanics and will be discussed in more detail in further Sections.
Wavepackets - The Superposition Principle in Action
Consider the wavefunction corresponding to a free electron traveling through a cathode ray tube. The electron leaves the cathode, shoots through the vacuum, and impinges on the screen. At an intermediate point in this process, it is moving through the vacuum and the wavefunction must be nonzero over some volume, but zero in the places the electron has not possibly reached yet, and zero in the places it has definitely left.
However, if the electron has a precise energy (which is all kinetic energy), it also has a precise momentum. De Broglie argued that this necessarily implies that the electron wave has a precise wavelength. However, since it is a free particle (\(V=0\), the only wave with a precise wavelength \(\lambda\) has the form
\[\psi (x,t) = A e^{i(kx - \omega t)} \label{timeI}\]
where \(k = \frac {2 \pi}{\lambda}\) and \(\omega = 2 \pi \nu\). The wavefunctions of Equation \ref{timeI} are the solutions to the full time-independent Schrödinger equation (not just the spatial component discussed above).
The problem with using the wavefunctions of Equation \ref{timeI} to represent free particles is that plane sine waves extend to infinity in both spatial directions, so cannot represent a particle whose wavefunction is nonzero in a limited region of space. Physically, that it must have a wavefunction that goes to zero far away in either direction. A localized wavefunction of this type is called a “wavepacket”. We shall discover that a wavepacket can be constructed by adding plane waves together. To represent a localized particle, we must superpose waves having different wavelengths. Now, the plane waves we add together will individually be solutions of the Schrödinger equation.
As discussed in previously for a classical wave equation, it quantum equivalent, i.e., Schrödinger equation (both time dependent and independent), are linear equations. That is, if \(\psi _1(x,y,z,t), \psi _2(x,y,z,t)\) are both solutions of the equation, then so is
\[\psi (x,y,z,t) = c_1 \psi _1(x,y,z,t) + c_2 \psi _2(x,y,z,t) \]
where \(c_1\) and \(c_2\) are arbitrary constants, as is easy to check. This previously called this property the Principle of Superposition.
The essential point is that in Schrödinger’s equation every term contains a factor \(\psi\), but no term contains a factor \(\psi ^2\) (or a higher power). That is what is meant by a “linear” equation. If the equation did contain a constant term, or a term including \(\psi ^2\), superposition wouldn’t work—the sum of two solutions to the equation would not itself be a solution to the equation.
In fact, we have been assuming this linearity all along: when we analyze interference and diffraction of waves, we just add the two wave amplitudes at each spot. For the double slit, we take it that if the wave radiating from one slit satisfies the wave equation, then adding the two waves together will give a new wave which also satisfies the equation.
Building Wavepackets
If we add together two sine waves with frequencies close together, we get "beats." This pattern can be viewed as a string of wavepackets. For example considering adding to sine waves together with spatial and temporal frequencies of \((k \pm \Delta k\)) and (\( \omega \pm \Delta \omega\)), respectively.
\[\sin \left[(k - \Delta k) x - (\omega - \Delta \omega) t \right] + \sin \left[ (k + \Delta k) x - ( \omega + \Delta \omega )t \right]) \label{WP1}\]
If we use the trigonometric addition formula, the sum in Equation \ref{WP1} can be simplified to
\[ 2 \sin (kx - \omega t ) \cos \left[ (\Delta k) x - (\Delta \omega)t \right] \label{beats}\]
Equation \ref{beats} exhibits the phenomenon of beats between waves close in frequency. The first term, \(\sin (kx - \omega t)\), oscillates at the average of the two frequencies. It is modulated by the slowly varying second term, often called the “envelope function”, which oscillates once over a spatial extent of order \(\pi / \Delta k\). This is the distance over which waves initially in phase at the origin become completely out of phase. Of course, going a further distance of order \(\pi / \Delta k\), the waves will become synchronized again.
That is, beating two close frequencies together breaks up the continuous wave into a series of packets, the beats. To describe a single electron moving through space, we need a single packet. This can be achieved by superposing waves having a continuous distribution of wavelengths, or wave numbers within of order \(\Delta k\), say, of \(k\). In this case, the waves will be out of phase after a distance of order \(\pi / \Delta k\), but since they have many different wavelengths, they will never get back in phase again.
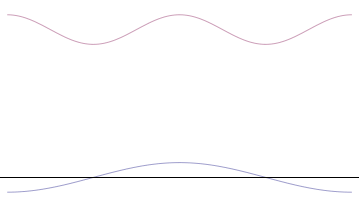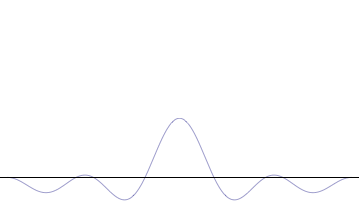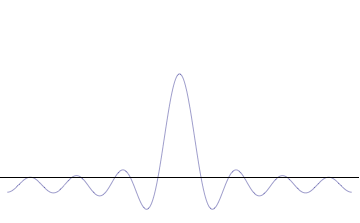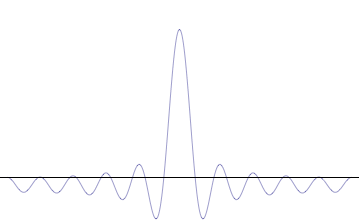
We have seen how two sine waves of equal amplitude close together in frequency produce beats: if the waves are in phase at the origin, as we go along the x-axis they gradually fall out of phase, and cancel each other at a distance \(x = \dfrac {\pi}{2 \Delta}\), where \(2 \Delta \) is the difference in \(k\) of the two \(\sin kx\) waves (Figure \(\PageIndex{3}\)). (For the moment, we are ignoring the time development of these waves: we’re just looking at t = 0.). If we continue along the x-axis to \(\dfrac {\pi}{\Delta}\), the two waves will be back in phase again, this is the next beat. Now, if instead of adding two waves, we add many waves, all of different \(k\), but with the \(k\)’s taken from some small interval of size of order \(\Delta k\), and all these waves are in phase at the origin, then, again, they will all stay more or less in phase for a distance of order \(x = \dfrac {\pi}{2 \Delta}\).
However, as we proceed past that point, the chances of them all getting back in phase again get rapidly smaller as we increase the number of different waves. This wavepacket perspective of a free particle is shown in Figure \(\PageIndex{4}\), where the wavefunction amplitude (both real and imaginary) is localized and tapers off on either side (contrast this image with Figure \(\PageIndex{1}\) that exhibits uniform amplitude over all space since it is an oscillatory eigenfunction.
Fortunately, there is a simple explicit mathematical realization of the addition of plane waves to form a localized function: the Gaussian wavepacket:
\[\psi (x,t = 0) = A \underbrace{e^{ik_0x}}_{\text{oscillating term}} \overbrace{e^{-x^2/2\Delta ^2}}^{\text{Gaussian envelope}}\]
where \(k_0\) is an average wavenumber. Topically, the equation for Gaussian wavepackets has an oscillating term with a Gaussian envelope function. This wavepacket wavefunction may be used to represent a localized electron with a negligible probability of finding the electron outside in a small section of length \(dx\) at \(x\)(Figure \(\PageIndex{3}\)).
.gif?revision=1)

