2.4: The General Solution is a Superposition of Normal Modes
- Page ID
- 92350
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Separate the wave equation into individual spatial and temporal problems and solve them.
- Demonstrate that the general solution can be a superposition of solutions (normal modes)
As discussed previously, the solutions to the string example \(u(x,t)\) for all \(x\) and \(t\) would be assumed to be a product of two functions: \(X(x)\) and \(T(t)\), where \(X(x)\) is a function of only \(x\), not \(t\) and \(T(t)\) is a function of \(t\), but not \(x\).
\[u(x,t)= X(x)T(t) \nonumber \]
By substituting the new product solution form into the original wave equation, one can obtain two ordinary differential equations (differential equation containing a function or functions of one independent variable and its derivatives). Each differential equation would involve only one of the independent variables (\(x\) or \(t\)).
Spatial Dependence of the Solution: \(X(x)\)
The boundary conditions for the string held to zero at both ends argue that \(u(x,t)\) collapses to zero at the extremes of the string. Unfortunately, when \(K>0\), the general solution to the wave equation results in a sum of exponential decays and growths that cannot achieve the boundary conditions (except for the trivial solution that \(u(x,t)=0\)); hence \(K<0\). This means we must introduce complex numbers due to the \(\sqrt{K}\) terms in Equation 2.2.5. So we can rewrite \(K\):
\[K = - p^2 \label{2.4.1} \]
and Equation 2.2.4b can be
\[\dfrac{d^2X(x)}{dx^2} +p^2 X(x) = 0 \label{2.4.2} \]
The general solution to differential equations of the form of Equation \(\ref{2.4.2}\) is Equation 2.2.5
\[X(x) = A e^{\sqrt{K}x} + B e^{-\sqrt{K}x} \label{2.4.3} \]
that when substituted with Equation \(\ref{2.4.1}\) give
\[X(x) = A e^{ipx} + B e^{-ipx} \label{2.4.4} \]
The complex exponentials can be expressed as trigonometric functions via Euler formula (\(e^{i \theta} = \cos \theta + i\sin \theta\))
\[X(x) = A \left[\cos (px) + i \sin (px) \right] + B \left[ \cos (px) - i \sin (px) \right] \nonumber \]
collecting like terms
\[X(x) = (A + B ) \cos (px) + i (A - B) \sin (px) \label{2.4.6} \]
Introduce new complex constants \(C=A+B\) and \(D=i(A-B)\) so that the general solution in Equation \(\ref{2.4.6}\) can be expressed as oscillatory functions
\[X(x) =C \cos (px) + D \sin (px) \label{2.4.7} \]
Verify that Equation \ref{2.4.3} is the general form for differential equations of the form of Equation \(\ref{2.4.2}\).
- Answer
-
In order to show that
\[X(x)=A e^{\sqrt{x} x}+B e^{-\sqrt{x} x} \label{2.2.4} \]
is a general solution to the differential equation
\[\frac{d^{2} X(x)}{d x^{2}}+p^{2} X(x)=0. \nonumber \]
We then have to take the second derivative of Equation \ref{2.2.4} and substitute it and the original function into the appropriate locations in Equation \ref{2.4.3} and verify that it does in fact equal \(0\).
First we have to take the first and then second derivative of Equation \ref{2.2.4}
\[\begin{array}{l}
{\dfrac{d}{d x}\left(A e^{\sqrt{k x}}+B e^{-\sqrt{k} x}\right)=\sqrt{k} A e^{\sqrt{k x}}-\sqrt{k} B e^{-\sqrt{k x}}} \\
{\dfrac{d^{2}}{d x^{2}}\left(A e^{\sqrt{k x}}+B e^{-\sqrt{k} x}\right)=k A e^{\sqrt{k x}}+k B e^{-\sqrt{k x}}}
\end{array} \nonumber \]Now that we have the second derivative of Equation \ref{2.2.4} we plug the relevant values into Equation \ref{2.4.2}
\[\begin{align*} \dfrac{d^{2} X(x)}{d x^{2}}+p^{2} X(x)=0 \\ k A e^{\sqrt{k} x}+k B e^{-\sqrt{k} x}+p^{2}\left(A e^{\sqrt{k} x}+B e^{-\sqrt{k} x}\right) \overset{?}{=} 0 \end{align*} \nonumber \]
We are given in Equation \ref{2.4.2} that
\[ k=-p^{2} \nonumber \]
So
\[p^{2}=-k \nonumber \]
Now we can plug that into our differential equation to simplify
\[\begin{align*} k A e^{\sqrt{k} x}+k B e^{-\sqrt{k} x} - k\left(A e^{\sqrt{k} x}+B e^{-\sqrt{k} x} \right) &\overset{?}{=} 0 \\[4pt] \bcancel{ k A e^{\sqrt{k x}}} + \cancel{k B e^{-\sqrt{k x}}} - \bcancel{k A e^{\sqrt{k x}}} - \cancel{k B e^{-\sqrt{k x}}} & \overset{\checkmark}{=} 0 \end{align*} \nonumber \]
As all of these terms cancel to equal 0, we prove that the solution given is a general solution to the differential equation. It is important to remember though that it is not the only solution to the differential equation.
Now let's apply the boundary conditions from Equation 2.2.7 to determine the constants \(C\) and \(D\). Substituting the first boundary condition (\(X(x=0)=0\)) into the general solutions of Equation \(\ref{2.4.7}\) results in
\[\begin{align} X(x=0) &= 0 \\[4pt] C \cos (0) + D \sin (0) &=0 \label{2.4.8a} \\[4pt] C + 0 &= 0 \label{2.4.8b} \\[4pt] C&=0 \label{2.4.8c} \end{align} \]
and substituting the second boundary condition (\(X(x=L)=0\)) into the general solutions of Equation \(\ref{2.4.7}\) results in
\[ X(x=L) = C \cos (pL) + D \sin (pL) = 0 \label{2.4.9} \]
we already know that \(C=0\) from the first boundary condition so Equation \(\ref{2.4.9}\) simplifies to
\[ D \sin (pL) = 0 \label{2.4.10} \]
Given the properties of sines, Equations \ref{2.4.9} simplifies to
\[ pL= n\pi \label{2.4.11} \]
with \(n=0\) is the trivial solution that we ignore so \(n = 1, 2, 3...\).
\[ p = \dfrac{n\pi}{L} \label{2.4.12} \]
Substituting Equations \(\ref{2.4.12}\) and \(\ref{2.4.8c}\) into Equation \(\ref{2.4.7}\) results in
\[X(x) = D \sin \left(\dfrac{n\pi x}{L} \right) \label{2.4.13} \]
Equation \(\ref{2.4.13}\) presents a set of solutions to the spatial part of the solution to the wave equation subject to the boundary conditions (Figure 2.4.1 ). This set of solutions is infinitely large with individual solutions that are distinguished from each other by the \(n\) parameter introduced to account for the boundary conditions. This number is an example of a "quantum number" that are ubiquitously in quantum mechanics and are uniquely defined for each system.
Time Dependence of the Solution: \(T(t)\)
A similar argument applies to the other half of the ansatz (\(T(t)\)) originally proposed for the classical wave equation was obtain from solving Equation 2.2.4a, which qualitatively resembles the original spatial differential equation solved above (Equation 2.2.4b).
\[ \dfrac{d^2T(t)}{dt^2} - Kv^2 T(t) = 0 \nonumber \]
However, the constraints extracted from solving spatial dependence apply to the time dependence. When Equations \(\ref{2.4.1}\) and \(\ref{2.4.12}\) are substituted into Equation 2.2.4a, a more simplified expression is obtained
\[ \dfrac{d^2T(t)}{dt^2} + p^2v^2 T(t) = \dfrac{d^2T(t)}{dt^2} + \left(\dfrac{n v \pi}{L}\right)^2 T(t) = 0 \label{2.4.14} \]
Define a new constant: \(\omega_n\)
\[\omega_n= \left(\dfrac{n v \pi}{L}\right) \label{2.4.15} \]
and substitute into Equation \(\ref{2.4.14}\)
\[ \dfrac{d^2T(t)}{dt^2} + \omega_n^2 T(t) = 0 \label{2.4.16} \]
This is the same functional form of Equation \(\ref{2.4.2}\)
\[ T(t) = E \cos (\omega_n t) + F \sin (\omega_n t) \label{2.4.17} \]
In contrast to the spatial dependence solution, we have no boundary conditions to use to identify the constants \(E\) and \(F\).
The Principle of Superposition
Now let's revisit the original ansatz solution to the classical wave equation (Equation 2.2.1), which can be substituted with Equations \(\ref{2.4.13}\) and \(\ref{2.4.17}\)
\[\begin{align} u(x,t) &= X(x)T(t) \label{2.4.19a}\ \\[4pt] &= \left[D \sin \left(\dfrac{n\pi x}{L} \right) \right] \left( E \cos (\omega_n t) + F \sin (\omega_n t) \right) \end{align} \label{2.4.18b} \]
we can collect constants again with \(G=DE\) and \(H=DF\) and introduce a \(n\) dependence to each since \(E\) and \(F\) may be \(n\) dependence.
\[u_n(x,t) = \left[ G_n \cos (\omega_n t) + H_n \sin (\omega_n t) \right] \sin \left(\dfrac{n\pi x}{L} \right) \label{2.4.19} \]
The functions represented in Equation \(\ref{2.4.19}\) are set of solutions including both spatial and temporal features that solve the wave equation of a string held tight on two ends.
The wave equation has a very important property: if we have two solutions to the equation, then the sum of the two is also a solution to the equation. It’s easy to check this:
\[ \dfrac{\partial^2 (f+g)}{\partial x^2} = \dfrac{\partial^2 f}{\partial x^2} + \dfrac{\partial^2 g}{\partial x^2} = \dfrac{1}{v^2} \dfrac{\partial^2f}{\partial t^2} +\dfrac{1}{v^2} \dfrac{\partial^2g}{\partial t^2} = \dfrac{1}{v^2} \dfrac{\partial^2(f+g)}{\partial t^2} \nonumber \]
Any differential equation for which this property holds is called a linear differential equation. Also note that \(af(x,t) + bg(x,t)\) is also a solution to the equation if \(a\), \(b\) are constants. So you can add together—superpose—multiples of any two solutions of the wave equation to find a new function satisfying the equation.
This important property is easy to interpret visually: if you can draw two wave solutions, then at each point on the string simply add the displacement \(u_n(x,t)\) of one wave to the other \(u_m(x,t)\)—the sum of the two waves together is a solution. So, for example, as two traveling waves moving along the string in opposite directions meet each other, the displacement of the string at any point at any instant is just the sum of the displacements it would have had from the two waves singly.
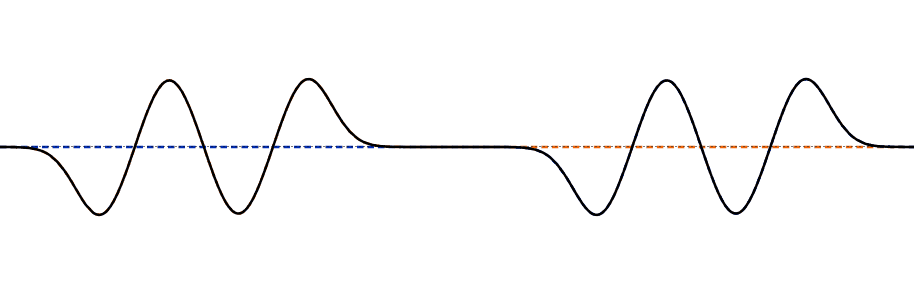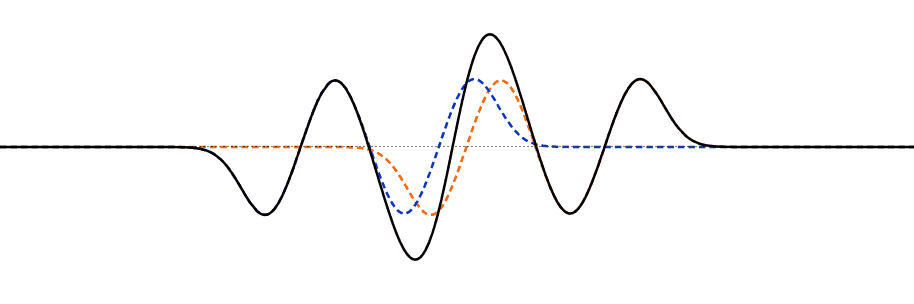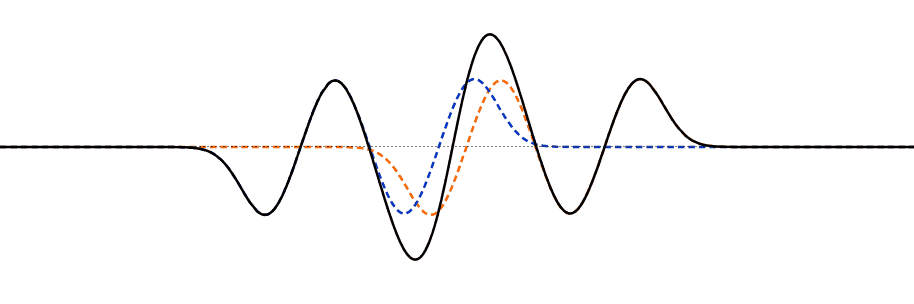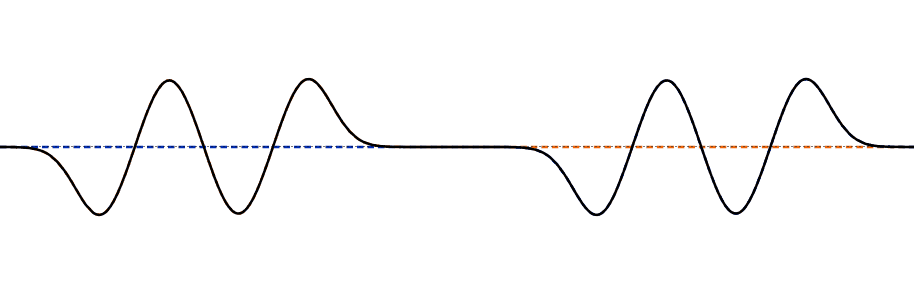
This simple addition of the displacements is interference, doubtless because if the waves meeting have displacements in opposite directions, the string will be displaced less than by a single wave. This is also called the Principle of Superposition.
The Principle of Superposition is the sum of two or more solutions is also a solution.
Since the wave equation is a linear homogeneous differential equation, the total solution can be expressed as a sum of all possible solutions described by Equation \(\ref{2.4.19}\).
\[\begin{align} u(x,t) &= \sum_{n=1}^{\infty} u_n(x,t) \label{2.4.20} \\[4pt] & = \sum_{n=1}^{\infty} \left( G_n \cos (\omega_n t) + H_n \sin (\omega_n t) \right) \sin \left(\dfrac{n\pi x}{L}\right) \label{2.4.21} \end{align} \]
Each \(u_n(x,t)\) solution is called a normal mode of the system and can be characterized via their corresponding frequencies \(\dfrac{n\pi}{L}\) with \(n=1,2,3...\). The spatial dependence of the first seven normal modes are shown in Figure 2.4.1 and are standing waves. The first term with \(n=1\) is typically called the fundamental and each subsequent modes is called an overtone or harmonic. The temporal dependence of the normal modes is sinusoidal with angular frequencies \(\omega_n\) that can be expanded to natural frequencies \(\nu_n\) via
\[ \nu_n = \dfrac{\omega_n}{2 \pi} = \dfrac{nv}{2L} \label{2.4.22} \]
Hence, as the spatial curvature of the normal mode increases, the temporal oscillation of that mode also increases. This is a common trait in quantum mechanical systems and is a direct consequence of the wave equation.

