26: Molecular Orbitals and Diatomics
- Page ID
- 65258
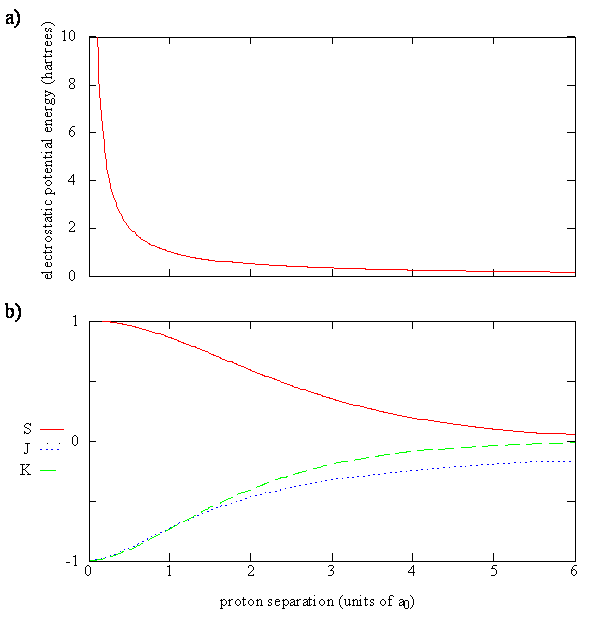
Last Lecture focused on the LCAO approximation for the \(H_2^+\) molecule. We solved for the bonding and antibonding LCAO-MOs, which was not hard. Solving for the energies of these molecular orbitals was a bit harder and depended on the bond length and three integrals (defined below for the \(\{| 1s \rangle \}\) basis set):
- The Overlap Integral: \[S(R)= \left \langle 1s_A | 1s_B \right \rangle\]
- The Coulomb Integral: \[J(R) = - \left \langle 1s_A | \dfrac {e^2}{4 \pi \epsilon _0 r_B } | 1s_A \right \rangle\]
- The Exchange Integral: \[K(R)= - \left \langle 1s_A | \dfrac {e^2}{4 \pi \epsilon _0 r_A } | 1s_B \right \rangle \]
The expression for the electronic energy (of a single electron in a single molecular orbital in this system) of the \(H_2^+\) molecule
\[E_{\pm} = E_H + \dfrac {e^2}{4\pi \epsilon _0 R} + \dfrac {J \pm K}{1 \pm S} \label {9.4.10}\]
The results formulas were for the bonding orbital
\[E_{+}= E_H + \dfrac {e^2}{4\pi \epsilon _0 R} + \dfrac{J+K}{1+S}\ \ \ \ \ (bonding)\nonumber \]
and for the antibonding orbital
\[E_{-}= E_H + \dfrac {e^2}{4\pi \epsilon _0 R} + \dfrac{J-K}{1-S}\ \ \ \ \ (antibonding) \nonumber\]
The energy of the molecular orbital (Equation \ref{9.4.10}) is a function of \(R\) since the three integrals outlines above are functions of \(R\) as is the Coulombic repulsion term. Equation \(\ref{9.4.10}\) tells us that the energy of the \(H_2^+\) molecule is
- the energy of a hydrogen atom plus \[E_H \label{eq1}\]
- the Coulombic repulsive energy of two protons plus \[\dfrac {e^2}{4\pi \epsilon _0 R} \label{eq2}\]
- some additional electrostatic interactions of the electron with the protons. \[\dfrac {J \pm K}{1 \pm S} \label{eq3}\]
These bonding interactions are given by Equation \ref{eq3}. To get a chemical bond (i.e., a stable H2+ molecule):
- \(\Delta E_{\pm} = E_{\pm} - E_H\) must be less than zero (otherwise it is lower energy to be a \(H\) atom and a \(H^+\) free proton, which no energy)
- The energy of the molecule must have a minimum, i.e. the bonding energy (Equation \ref{eq3}) must be sufficiently negative to overcome the positive repulsive energy of the two protons (Equation \ref{eq2} for some value of \(R\). For large \(R\), these both terms (Equations \ref{eq2} and \ref{eq3}) are zero, and for small \(R\), the Coulombic repulsion (Equation \ref{eq2}) of the protons rises to infinity.
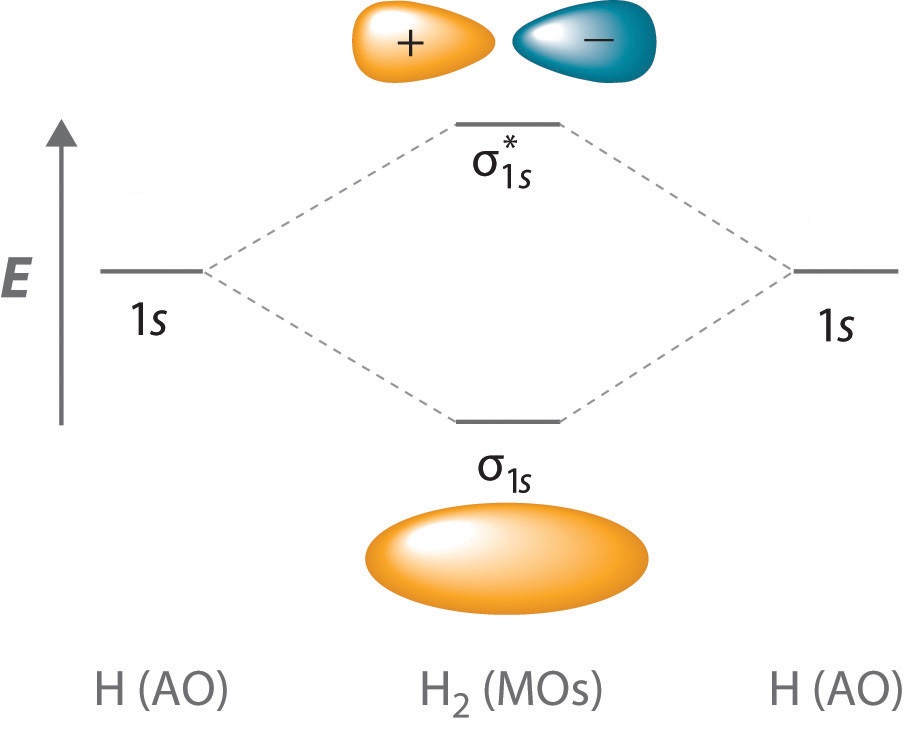
The \(\psi_+\) molecular orbital has a lower energy than either of the hydrogen 1s atomic orbitals. Conversely, the \(\psi_-\) molecular orbital has a higher energy than either of the hydrogen 1s atomic orbitals.
Equation \(\ref{9.4.10}\) can be rewritten as
\[ \Delta E_{\pm} = E_{\pm} - E_H = \dfrac {e^2}{4\pi \epsilon _0 R} + \dfrac {J \pm K}{1 \pm S} \label {10.31}\]
which shows energy of H2+ relative to the energy of a separated hydrogen atom and a proton. For the electron in the \(\psi_-\) orbital, the energy of the molecule, \(E_{el}(R)\), always is greater than the energy of the separated atom and proton.
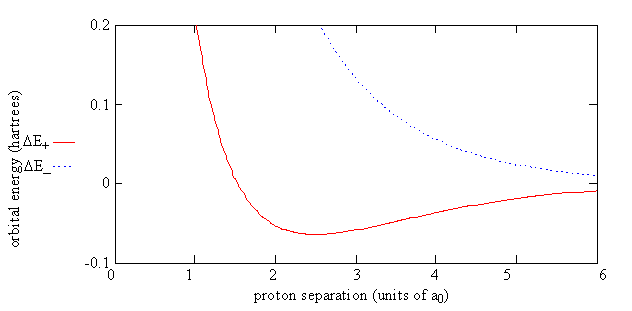
For the electron in the \(\psi_-\) orbital, the energy of the molecule, \(E_{el}(R)\), always is greater than the energy of the separated atom and proton. That is, nature will prefer a bond to be formed to lower the energy of the system.
Secular Equations in Molecular Orbitals (MOs within the linear Variational Method)
This picture of bonding in H2+ in the previous section is very simple, but gives reasonable results when compared to an exact calculation. The equilibrium bond distance is 134 pm compared to 106 pm (exact), and a dissociation energy is 1.8 eV compared to 2.8 eV (exact). One way to improve this approach is to use a bigger basis set, e.g.,
\[| \psi_J \rangle = c_{J,1} 1s_A + c_{J,2} 1s_B + c_{J,3} 2s_A + c_{J,4} 2s_B + c_{J,5} 2p_{z,A} + c_{J,6} 2p_{z,B} \label{bigger}\]
Above is a 6-element (atomic orbital) basis set using both n=1 and n=2 atomic orbitals. The expressions above for the energy of \(H_2^+\) can be formatted in terms of a basis set of any number of functions (only six are in the LCAO expansion in Equation \ref{bigger}).
Following the LCAO approximation, the jth molecular orbital can be expressed as a linear combination of many atomic orbitals {\(\{\phi_i\}\)}:
\[\psi_J = \sum_i a_{J,i} \phi_i \label{9.5.1}\]
The energy of the non-normalized molecular orbital can be calculated from the expectation value integral of the Hamiltonian,
\[E_{J} = \dfrac{\left \langle \psi _{J} | \hat {H} _{elec} | \psi _{J} \right \rangle}{\left \langle \psi _{J} | \psi _{J} \right \rangle} \label {9.5.2}\]
In this case, the denominator (\(\left \langle \psi _{J} | \psi _{J} \right \rangle\)) is left in; if the MOs are normalized we do not need to explicitly address.
After substituting the LCAO expansion for \(\phi_J\) (Equation \ref{bigger}) into the energy expression (Equation \ref{9.5.2}):
\[\begin{align} E_{J} &= \dfrac{\left \langle \displaystyle \sum_i a_{J,i}^* \phi_i | \hat {H} _{elec} | \displaystyle \sum_j a_{J,i} \phi_j \right \rangle}{\left \langle \displaystyle \sum_i a_{J,i}^* \phi_j | \displaystyle \sum_j a_{J,j} \phi_j\right \rangle} \label {9.5.3} \\[4pt] &= \dfrac{\displaystyle \sum_{i,j} a_{J,i}^* a_{J,j} \left \langle \phi_i | \hat {H} _{elec} | \phi_j \right \rangle}{\displaystyle \sum_{i,j} a_{J,i}^* a_{J,j} \left \langle \phi_i | \phi_j\right \rangle} \label {9.5.4} \\[4pt] &= \dfrac{ \displaystyle \sum_{i,j} a_{J,i}^* a_{J,j} H_{ij}}{ \displaystyle \sum_{i,j} a_{J,i}^* a_{J,j} S_{ij} } \label {9.5.5} \end{align}\]
Following the varitional theorem, to determine the coefficients of the LCAO expansion \(a_i\), we need to minimize \(E_J\)
\[ \dfrac{\partial E_J}{\partial a_k} = 0 \label{9.5.6}\]
for all \(k\). This requires solving \(N\) linear equations to hold true (where N is the number of atomic orbitals in the basis)
\[ \sum_{i=1}^{N} a_i (H_{ki} - ES_{ki}) = 0 \label{9.5.7}\]
These equations are the secular equations and were discussed previously in the context of linear variational method approximation.
For the two function basis set, like that discussed above, these secular equtations can be written out as
\[\begin{array}{rcl} a_1(H_{11} - ES_{11}) + a_2(H_{12} - ES_{12}) & = & 0 \\ a_1(H_{12} - ES_{12}) + a_2(H_{22} - ES_{22}) & = & 0 \end{array} \label{9.5.8}\]
where \(a_1\) and \(a_2\) are the coefficients in the linear combination of the atomic orbitals used to construct the molecular orbital. Writing this set of homogeneous linear equations in matrix form gives
\[\begin{pmatrix} H_{11} - ES_{11} & H_{12} - ES_{12} \\ H_{12} - ES_{12} & H_{22} - ES_{22} \end{pmatrix} \begin{pmatrix} a_1 \\ a_2 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \end{pmatrix} \label{9.5.9}\]
Solving this requires finding the N roots of a polynomial of order \(N\) (i.e., N different satisfactory values of E). For each \(E_J\) there is a different set of coefficients, \( { a_{ij} } \) where i runs over all functions in the basis functions, and \(J\) runs over molecular orbitals, each having energy \(E_J\). Solve the set of linear equations using that specific \(E_J\) to determine \(a_{ij}\) values.
- Select a set of N basis functions
- Determine all N( N –1)/2 values of both \(H_{ij}\) and \(S_{ij}\)
- Form the secular determinant; determine \(N\) roots \(E_j\) of secular equation
- For each \(E_J\) solve the set of linear equations to determine the basis set coefficients \(a_{ij}\) for the j-th molecular orbital
Molecules follow the Pauli Exclusion Principle and Hund's Rules
Just as for atoms, each electron in a molecule can be described by a product of spin-orbitals. Since electrons are fermions, the electronic wavefunction must be antisymmetric with respect to the permutation of any two electrons. A Slater determinant containing the molecular spin orbitals produces the antisymmetric wavefunction. For example for two electrons,
\[\Psi (r_1, r_2) = \dfrac{1}{\sqrt{2}} \begin {vmatrix} \psi _A (r_1) \alpha (1) & \psi _B (r_1) \beta (1) \\ \psi _A (r_2) \alpha (2) & \psi _B (r_2) \beta (2) \end {vmatrix} \label{9.6.2}\]
Solving the Schrödinger equation in the orbital approximation will produce a set of spatial molecular orbitals, each with a specific energy, \(\epsilon\). Following the Aufbau Principle, two electrons with different spins ( \(\alpha\) and \(\beta\), consistent with the Pauli Exclusion Principle discussed for muliti-electron atoms) are assigned to each spatial molecular orbital in order of increasing energy. For the ground state of the 2n electron molecule, the n lowest energy spatial orbitals will be occupied, and the electron configuration will be given as \(\psi ^2_1 \psi ^2_2 \psi ^2_3 \dots \psi ^2_n\). The electron configuration also can be specified by an orbital energy level diagram as shown in Figure \(\PageIndex{1}\). Higher energy configurations exist as well, and these configurations produce excited states of molecules. Some examples:

Reflection in 1D
Before we discussed the symmetry of wavefunctions upon refection (i.e., \(x \rightarrow -x\) and called them "odd" or "even" (or neither, but let's ignore that symmetry).
\[\hat{R} | \psi(x) \rangle = |\psi(-x) \rangle = (+1) | \psi(x) \rangle \,\,\, even\]
and
\[\hat{R} | \psi(x) \rangle = |\psi(-x) \rangle = (-1) | \psi(x) \rangle \,\,\, odd\]
Circular Symmetry (\(\sigma\) symmetry)
Circular symmetry is a type of continuous symmetry for a planar object that can be rotated by any arbitrary angle and map onto itself.
\[\hat{\Theta} | \psi(r, \,\theta, \,\phi) \rangle = \psi(r, \,\theta+\theta_1, \,\phi) \rangle = | \psi(r, \,\theta, \,\phi) \rangle \,\,\, \text{circular symmetric}\]
If a molecular orbital is symmetrical with respect to circular symmetry, it is called a sigma (\(\sigma\)) orbital.
Reflection or 180° Rotation Symmetry (\(\pi\) symmetry)
Circular symmetry is a type of continuous symmetry for a planar object that can be rotated by any arbitrary angle and map onto itself.
\[\hat{\Pi} | \psi(r, \,\theta, \,phi) \rangle = \psi(r, \,\theta+\pi, \,\phi) \rangle = (-1) | \psi(r, \,\theta, \,\phi) \rangle \,\,\, \text{circular symmetric}\]
A MO will have π symmetry if the orbital is asymmetric with respect to a \(\pi\) rotation (180°) about the internuclear axis. This means that rotation of the MO about the internuclear axis will result in a phase change.
If a molecular orbital is symmetrical with respect to circular symmetry, it is called a pi (\(\pi\)) orbital.
Center of Inversion
We can introduce another symmetry: the center of inversion (i.e., \(x, \,y, \,z \rightarrow -x, \,-y, \,-z\). Under this operator, we may have "gerade" and "ungerade" symmetry (or neither, but let's ignore that symmetry).
\[\hat{I} | \psi(x, \,y, \,z) \rangle = \psi(-x, \,-y, \,-z) \rangle = (+1) | \psi(x, \,y, \,z) \rangle \,\,\, gerade\]
and\[\hat{I} | \psi(x, \,y, \,z) \rangle = \psi(-x, \,-y, \,-z) \rangle = (-1) | \psi(x, \,y, \,z) \rangle \,\,\, ungerade\]
If a molecular orbital is symmetrical with respect to inversion, it has a subscript g (gerade, for even). If it is asymmetrical with respect to inversion, it is given a subscript u (ungerade, for uneven).
Bond Order
Bond order is the net number of bonding electrons in a molecule. is defined as one-half the net number of bonding electrons:
\[ \text{bond order}=\dfrac{\text{number of bonding electrons} - \text{number of antibonding electrons}}{2} \label{9.8.1} \]
To calculate the bond order of H2, we see from Figure 9.8.1 that the σ1s (bonding) molecular orbital contains two electrons, while the \( \sigma _{1s}^{\star } \) (antibonding) molecular orbital is empty. The bond order of H2 is therefore
\( \dfrac{2-0}{2}=1 \label{9.8.2} \)
This result corresponds to the single covalent bond predicted by Lewis dot symbols. Thus molecular orbital theory and the Lewis electron-pair approach agree that a single bond containing two electrons has a bond order of 1. Double and triple bonds contain four or six electrons, respectively, and correspond to bond orders of 2 and 3. We can use energy-level diagrams to describe the bonding in other pairs of atoms and ions where n = 1, such as the H2+ ion, the He2+ ion, and the He2 molecule. Again, we fill the lowest-energy molecular orbitals first while being sure not to violate the Pauli principle or Hund’s rule.

| Species | Electron Configuration | Bond Order | Bond Length (pm) | Bond Energy (kJ/mol) |
|---|---|---|---|---|
| H2+ | \((σ_{1s})^1\) | 1/2 | 106 | 269 |
| H2 | \((σ_{1s})^2\) | 1 | 74 | 436 |
| He2+ | \( \left (\sigma _{1s} \right )^{2}\left (\sigma _{1s}^{\star } \right )^{1} \) | 1/2 | 108 | 251 |
| He2 | \( \left (\sigma _{1s} \right )^{2}\left (\sigma _{1s}^{\star } \right )^{2} \) | 0 | 5,500 | \(4.6 \times 10^{−5}\) |
With a total of four valence electrons, both the σ1s bonding and \( \sigma _{1s}^{\star } \) antibonding orbitals must contain two electrons. This gives a \( \left (\sigma _{1s} \right )^{2}\left (\sigma _{1s}^{\star } \right )^{1} \) electron configuration, with a predicted bond order of (2 − 2) ÷ 2 = 0, which indicates that the He2 molecule has no net bond and is not a stable species (covalent bonding-wise at least).

