10: Expectation values, 2D-PIB and Heisenberg Uncertainty Principle (Lecture)
- Page ID
- 93435
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Last lecture focused on gaining an intuition of wavefunctions with an emphasis on the energies of the particle in the box (PIB) model. We continued the discussion of the PIB and the intuition we want from the model system. We revised the time-dependent solutions to the model system (which is always there). We emphasized that the total wavefunction must be oscillating in time (although we often ignore that in this class) and that it has both a real and imaginary component (we will revisit that again later on). We discussed the symmetry of functions and how to use symmetry of integrands to simply integrations. We used that fact to justify (in part) orthogonality, which is a powerful (blow your mind) fact that the eigenstates of an operator will be orthogonal.
\[\int_{0}^{L}\psi _{m}(x)\psi _{n}(x)dx=0\: \: \: if\: \: \: m \neq n \label{3.5.19}\]
This is really cool as we will see.
Expectation Value of Position of Particle in a Box (with n=1)
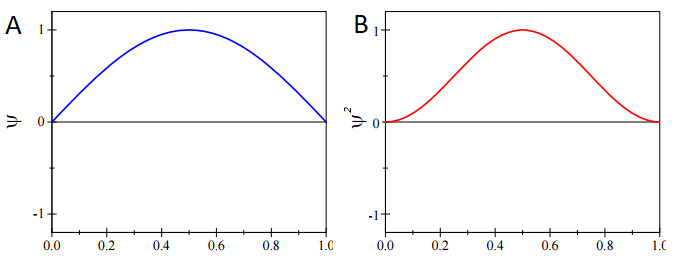
For the ground-state particle in a box wavefunction with \(n=1\):
\[\psi_{n=1} = \sqrt{\dfrac{2}{L}} \sin \left(\dfrac{\pi x}{L} \right) \label{PIB}\]
This state has the following probability distribution:
\[\psi^*_{n=1} \psi_{n=1} = \dfrac{2}{L} \sin^2 \left(\dfrac{\pi x}{L} \right)\]
In general the expectation value is the measurable for an operator
\[ \langle o \rangle = \int _{-\infty}^{+\infty} \psi^* \hat{O} \psi \, dx \label{expect}\]
The expectation value for position with the \(\hat{x} = x\) operation for this any wavefunction (Equation \(\ref{expect}\)) is
\[ \langle x \rangle = \int _{-\infty}^{+\infty} \psi^* x \psi \, dx \]
which for the ground-state wavefunction (Equation \(\ref{PIB}\)) shown in Figure \(\PageIndex{1}\) is
\[\begin{align} \langle x \rangle &= \int _{-\infty}^{+\infty} \sqrt{\dfrac{2}{L}} \sin \left(\dfrac{\pi x}{L} \right) x \sqrt{\dfrac{2}{L}} \sin \left(\dfrac{\pi x}{L} \right) \, dx \\[4pt] &= \dfrac{2}{L} \int _{-\infty}^{+\infty} x \sin^2 \left(\dfrac{\pi x}{L} \right) \label{GSExpect} \end{align}\]
You can do this equation, but you can see via symmetry that
\[ \langle x \rangle = \dfrac{L}{2}\]
A wavefunction gives you the probability of a particle to be seen somewhere. If it's not confined to be in some region, like a potential well or something, then it has a probability to be seen anywhere in the space. That's why the integration runs from \(−∞\) to \(+∞\) (remember that you could never pinpoint a quantum mechanical particle in space). That can be converted to a finite volume of space if the confinement is strong. For example, in the case of a particle in an infinite potential well, the boundary condition is that the wavefunction should vanish at the potential well boundaries.
Expectation Value of Momentum of Particle in a Box
What is the average momentum of a particle in the box? We start with Equation \(\ref{expect}\) and use the momentum operator
\[\hat{p}_{x}=-i\hbar\dfrac{\partial}{\partial x}\label{3.2.3a}\]
We note that the particle-in-a-box wavefunctions are not eigenfunctions of the momentum operator (Exercise \(\PageIndex{4}\)). However, this does not mean that Equation \(\ref{expect}\) is inapplicable as Example \(\PageIndex{2}\) demonstrates.
Even though the wavefunctions are not momentum eigenfunctions, we can calculate the expectation value for the momentum. Show that the expectation or average value for the momentum of an electron in the box is zero in every state (i.e., arbitrary values of \(n\)).
- Strategy:
-
First write the expectation value integral (Equation \(\ref{expect}\)) with the momentum operator. Then insert the expression for the wavefunction and evaluate the integral as shown here.
- Answer
-
\[\left \langle P \right \rangle = \int \limits ^L_0 \psi ^*_n (x) \left ( -i\hbar \dfrac {d}{dx} \right ) \psi _n (x) dx\]
\[ = \int \limits ^L_0 \left (\dfrac {2}{L} \right )^{1/2} \sin (\dfrac {n \pi x}{L}) \left ( -i\hbar \dfrac {d}{dx} \right ) \left (\dfrac {2}{L} \right )^{1/2} \sin (\dfrac {n \pi x }{L} ) dx \]
\[ = -i \hbar \left (\dfrac {2}{L} \right ) \int \limits ^L_0 \sin (\dfrac {n \pi x}{L}) \left ( \dfrac {d}{dx} \right ) \sin (\dfrac {n \pi x}{L}) dx\]
\[ = -i \hbar \left (\dfrac {2}{L} \right ) \left ( \dfrac {n \pi}{L} \right ) \int \limits ^L_0 \sin (\dfrac {n \pi x}{L}) \cos (\dfrac {n \pi x}{L}) dx\]
\[= 0\]
Note that this makes sense since the particles spends an equal amount of time traveling in the \(+x\) and \(–x\) direction.
- Interpretation:
-
It may seem that this means the particle in a box does not have any momentum, which is incorrect because we know the energy is never zero. In fact, the energy that we obtained for the particle-in-a-box is entirely kinetic energy because we set the potential energy at 0. Since the kinetic energy is the momentum squared divided by twice the mass, it is easy to understand how the average momentum can be zero and the kinetic energy finite
Time to Bring in the Heavy Guns: Dirac Notation
Kets
In Dirac’s notation what is known is put in a ket, \(| \, \rangle\). So, for example, \(| p \rangle\) expresses the fact that a particle has momentum \(p\). It could also be more explicit: \(| p=2 \rangle\), the particle has momentum equal to 2; \(| x=1.23 \rangle\), the particle has position 1.23. \(| \Psi \rangle\) represents a system in the state \( \Psi \) and is therefore called the state vector. The ket can also be interpreted as the initial state in some transition or event.
Bras
The bra \(\langle \, | \) represents the final state or the language in which you wish to express the content of the ket \(| \, \rangle\). For example,\( \langle 0.25 | \Psi \rangle\) is the probability amplitude that a particle in state \( \Psi\) will be found at position \(x = 0.25\). In conventional notation we write this as \( \Psi(x=0.25) \), the value of the function \( \Psi \) at \(x\)=0.25. The absolute square of the probability amplitude, \( \left| \langle x=0.25| \Psi \rangle \right|^2\), is the probability density that a particle in state \( \Psi \) will be found at \(x\) = 0.25. Thus, we see that a bra-ket pair can represent an event, the result of an experiment. In quantum mechanics an experiment consists of two sequential observations - one that establishes the initial state (ket) and one that establishes the final state (bra).
Bra-Ket Pairs
If we write \( \langle x| \Psi \rangle \), we are expressing \( \Psi \) in coordinate space without being explicit about the actual value of \(x\). \(\langle 0.25 | \Psi \rangle \) is a number, but the more general expression \(\langle x | \Psi \rangle \) is a mathematical function, a mathematical function of \(x\), or we could say a mathematical algorithm for generating all possible values of \( \langle x| \Psi \rangle \), the probability amplitude that a system in state \( | \Psi \rangle \) has position \(x\).
Heisenberg's Uncertainty Principle Redux
This Heisenberg Uncertainty Principles was originally introduces as
\[ \begin{align} \Delta{p_x}\Delta{x} &\ge \dfrac{h}{4\pi} \\[4pt] &\ge \dfrac{\hbar}{2} \label{1.9.5} \end{align}\]
with \(\hbar = \frac{h}{2\pi}= 1.0545718 \times 10^{-34}\; m^2 \cdot kg / s\).
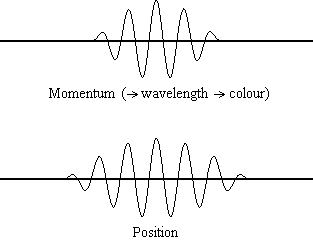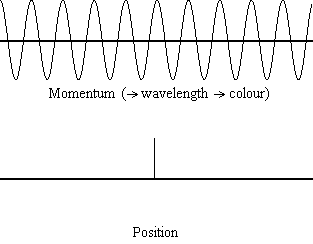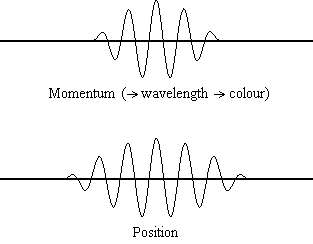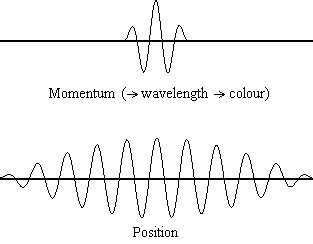
Equation \(\ref{1.9.5}\) relates the uncertainty of momentum and position. An immediate questions that arise is if \(\Delta x\) represents the full range of possible \(x\) values or if it is half (e.g., \(\langle x \rangle \pm \Delta x\)). \(\Delta x\) is the standard deviation and is a statistic measure of the spread of \(x\) values. The use of half the possible range is more accurate estimate of \(\Delta x\). Later, we can show that once a wavefunction can be constructed to describe the system, then both \(x\) and \(\Delta x\) can be explicitly derived.
In quantum mechanics,\(\langle x \rangle\) is the expected value of \(x\), which is the idea of a mean value in statistics. The expected value \(\langle x \rangle\) is equal to
\[\langle x \rangle = \int_{-\infty}^{\infty} \psi^* x \psi \,dx\]
where the wavefunctions are normalized (to satisfy the Born interpretation of wavefunctions)
\[\int_{-\infty}^{\infty} \psi^* \psi \,dx = 1 \]
This can be generalized to any operator such that
\[\langle \hat{A} \rangle= \int_{-\infty}^{\infty} \psi^* \hat{A} \psi \, dx \label{5}\]
The expected value of \(x\) in the 1D Particle in a Box problem can be found, because we know \(\psi (x)\), and we are given the operator \(\hat{x}\). Thus,
\[\langle x \rangle = \int_{-\infty}^{\infty} \psi^* (x) \hat{x} \psi (x) dx = \int_0^L \sqrt{\frac {2}{L}} \sin \left(\frac{n\pi x}{L}\right) x \sqrt{\frac {2}{L}} \sin \left(\frac{n\pi x}{L} \right)dx = \frac {2}{L} \int_0^a x\cdot \sin^2\left(\frac {n\pi x}{L}\right)dx \label{6}\]
Following through with the integral ultimately results in \(\langle x \rangle = L/2\), for all \(n\) values. The variance of the expected value of \(x\), represented as \(\sigma^2_x\) can be found by taking the difference of \(\langle x^2 \rangle\) and \(\langle x \rangle^2\), which is a measure of the "spread of the distribution" (see Worksheet #1) and is given by
\[ \langle \sigma_x^2 \rangle = \int_{a}^{b} (x-\langle x \rangle )^2 \psi^* \psi dx \label{5eq}\]
By using the same method to find \(\langle x \rangle\), Equation \(\ref{6}\) is solved to equal
\[\langle x^2 \rangle = \dfrac {L^2}{3} - \dfrac {L^2}{2n^2 \pi^2}\]
Square rooting the variance gives the standard deviation
\[\sigma_x = \sqrt{ \left(\dfrac {L}{2\pi n} \right)^2 \left(\dfrac{\pi^2 h^2}{3} -2\right)}.\]
The standard deviation for momentum is found in a similar fashion. Multiplying the resulting \(\sigma_p\) and \(\sigma_x\) gives Heisenberg's uncertainty principle product:
\[\sigma_x \sigma_p \geq \hbar/2\]
We can substitute the standard deviation for the uncertainty in the Heisenberg expression
\[\sigma_x = \Delta x\]
which provides a quantitative mechanism to interpret the uncertainty relationship.
The uncertainty of a position of a particle (\(\Delta x\)) is defined as
\[ \Delta x = \sqrt{ \langle x^2 \rangle - \langle x \rangle ^2} \]
For the particle in the box at the ground eigenstate (\(n=1\)), what is the uncertainty in the value \( x \)?
- Step 1: expectation value of the position
-
The expectation value of the position operator is:
\[\langle \hat{x}\rangle = \int_{0}^{a}\psi_n^*\hat{x}\psi_n dx\label{1}\]
or in Dirac notation
\[\langle \hat{x}\rangle = \langle n | \hat{x} | n \rangle\]
which expands to
\[\langle \hat{x}\rangle = \dfrac{2}{a}\int_{0}^{a}x\sin^2\dfrac{\pi x}{a}dx = \dfrac{a}{2}\tag{2}\]
Where we used the half angle formula and integration by parts to compute the integral.
- Step 2: expectation value of the position operator squared
-
The expectation value of the position operator squared is:
\[\langle \hat{x^2}\rangle = \int_{0}^{a}\psi_n^*\hat{x^2}\psi_n dx\label{3}\]
or in Dirac notation
\[\langle \hat{x}\rangle = \langle n | \hat{x^2} | n \rangle\]
which expands to
\[\langle \hat{x^2}\rangle = \dfrac{2}{a}\int_{0}^{a}x^2\sin^2\dfrac{\pi x}{a}dx = \dfrac{a^2}{3} - \dfrac{a^2}{2\pi^2}\tag{4}\]
Again we used the half angle formula and integration by parts to compute this integral.
- Answer
-
\[\Delta x = \sqrt{\langle \hat{x^2}\rangle - \langle \hat{x}\rangle^2 } \label{12}\]
Now insert \(\langle \hat{x^2}\rangle\) and \(\langle \hat{x}\rangle^2\).
\[\Delta x =\sqrt{\dfrac{a^2}{3} - \dfrac{a^2}{2\pi^2} - \dfrac{a^2}{4}}=a\sqrt{\dfrac{1}{12}-\dfrac{1}{2\pi^2} }=0.18a\]
Prove the following equality
\[ \langle \sigma_x^2 \rangle = \langle x^2 \rangle - \langle x \rangle^2\]

