3.6: IR and Raman Activity
- Page ID
- 366584
Selection Rule for IR
Recall, that for IR activity, we require that
\[\left(\frac{d \mu}{d q}\right)_{q_{\text {eq }}} \neq 0 \nonumber \]
If motion along the normal coordinate does not change the dipole moment, the transition is forbidden. In order for \(μ\) to be changed by the normal coordinate, at lease on of the following must be non-zero!
\[\langle v=0|\hat{x}| v \neq 0\rangle \nonumber \]
\[\langle v=0|\hat{y}| v \neq 0\rangle \nonumber \]
\[\langle v=0|\hat{z}| v \neq 0\rangle \nonumber \]
integrated over \(q\), the normal coordinate. This is since \(μ\) is a vector that transforms as x, y, z in the point group. The polarization of the IR transition is determined by which transition integral is non-zero. This is very much like the criterion for an electronically allowed transition.
All \(|v=0\rangle\) are a1 (totally symmetric) and \(|v=1\rangle\) has the same symmetry as the singly excited normal mode, \(q\). Since
\[A_{1} \otimes \Gamma_{x, y, z} \otimes \Gamma_{q} \supset A_{1} \nonumber \]
The transition will be IR active if the normal mode symmetry belongs to the same irreducible representation as x, y, or z for the point group of the molecule. This can be applied immediately to H2O.
Water has three vibrational modes.
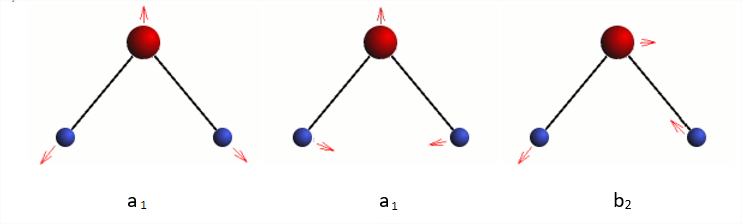
Three normal modes of water
Whether any of these modes is active in the infrared region of the spectrum is the question. This is determined by evaluating the quantum mechanical transition probability integral,
\[ P = e \int \Psi^f (vib) \hat{q} \Psi^i (vib) d \tau \nonumber \]
where q is the spatial coordinate and is either x, y, or z. If this integral is non-zero the transition is allowed. Group theory enables us to determine if the integral is non-zero as follows. We evaluate the direct product (note the similarity to the quantum mechanical transition probability integral) ΓvibfΓqΓvibi and if it turns out to be equal to, or contain, the irreducible representation A1 then the transition is allowed. If the direct product isn't equal to or contain A1 then the transition is forbidden.
Γvibi, the representation for the ground state is always equal to A1 and Γvibf is always equal to A1 and Γvibf has the symmetry of the vibrational mode being excited, which in our case is either A1 or B2. Thus we can see that a vibrational mode will be infrared active if it belongs to the same symmetry species as one of the Cartesian coordinates. You should verify that this is correct and also be able to show that all three vibrational modes of the water molecule are infrared active.
Selection Rule for Raman
Recall, for Raman activity, there must be a change in the polarizability with respect to the normal mode.
The components of the polarizability transform as the quadratic functions of x,y,z. i.e. x2, y2, z2, xy, xz, yz or combinations thereof (x2-y2). Thus we require that for the polarizability operator to transform as one of the quadratic terms e.g.
with
Thus since has the same symmetry as the singly excited normal mode, q. The transition integrals we know and love will be:
for at least one representation of polarization. At least one quadratic form transforms as each one of the irreducible representations. Therefore, all possible vibrations of any C2v molecule will be Raman allowed. But what about other point groups?
Centrosymmetric molecules – exclusion rules
There are important examples for which the IR allowed and Raman allowed transitions are mutually exclusive. There are molecules having a center of inversion. In this case, there normal coordinates, \(q\), must be either \(g\) or \(u\), depending on their behavior toward the \(\hat{i}\) operation. Thus \(|v=1\rangle\) must be either \(g\) or \(u\), while \(|v=0\rangle\) will always be \(g\).
In centrosymmetric molecules, the x,y,z operators are u-operators, while all components of \(\hat{P}\) are g-operators (go look it up on the Oh point group character table!) i.e.
\[\hat{x}^{2}=(-x)^{2} \quad \therefore \text { g symmetry } \nonumber \]
\[\hat{x}=-(-x) \quad \therefore \text { u symmetry } \nonumber \]
This symmetry behavior leads to the rule for centrosymmetirc molecules. Excitation of g-normal modes are forbidden in the IR, while excitation of u-normal modes are forbidden in Raman.
Carbon Dioxide is a linear triatomic molecule with 3N-5=4 normal modes:
e.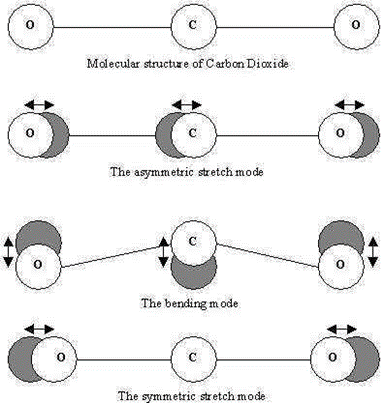
The point group is D∞h and the irreducible representations are \(\Sigma_{g}^{+}\), \Sigma_{u}^{+}, and \(\Pi_{u}\) respectively. Thus only asymmetric stretch and bends are found in the IR, while only the symmetric stretch is found in Raman spectra.
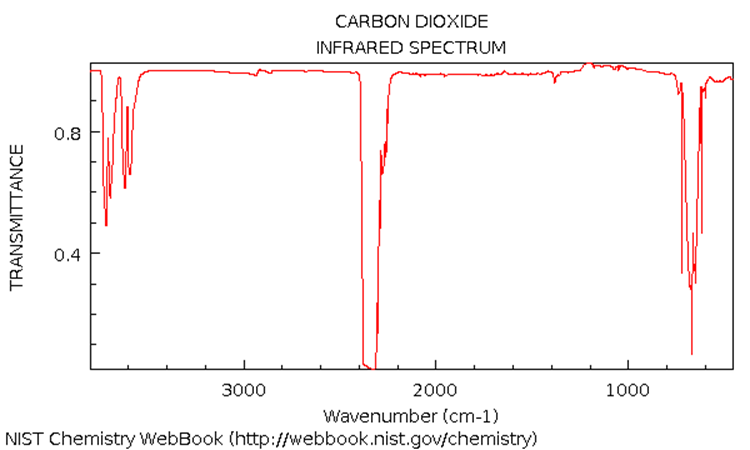
The IR spectrum of \(\ce{CO2}\) (4.0 kPa total pressure) is shown below. Note these extra bands: v3+v1=3610 cm-1 and v3+2*v2=3710 cm-1
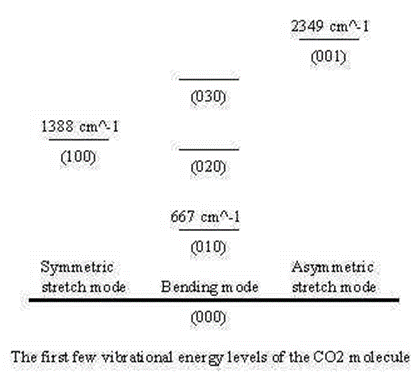
Vibrational frequency nomenclature
The \(3N-5\) (5) fundamental frequencies are usually numbered sequentially, \(\nu_1\), \(\nu_2\), \(\nu_3\),.. \(\nu_{3N-6}\). The convention is that the highest frequencies of totally symmetric vibrations in \(\nu_1\) follow all other totally symmetric vibrations in order of decreasing frequency. Once all totally symmetric vibrations are numbers, the next number goes to the highest frequency non-symmetric vibration.
For H2O:
- ν1 is the “symmetric stretch”
- ν2 is the “asymmetric stretch”
- ν3 is the “symmetric bend”
Exception, the bending mode of a linear molecule is ν2
For CO2:
- ν1 is the “symmetric stretch”
- ν2 is the “symmetric bend”
- ν3 is the “asymmetric stretch”
If IR and Raman spectra consisted only of fundamental and overtones, spectra would be easier to assign, but combinations bands, ν1 ± ν2 and overtones 2 ν1 also appear, complicating the assignment of the fundamental frequencies.

