3.5: Classification of Normal Modes
- Page ID
- 366583
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
Normal modes are used to describe the different vibrational motions in molecules. Each mode can be characterized by a different type of motion and each mode has a certain symmetry associated with it. Group theory is a useful tool in order to determine what symmetries the normal modes contain and predict if these modes are IR and/or Raman active. Consequently, IR and Raman spectroscopy is often used for vibrational spectra.
The normal modes that come out of the normal mode analysis are grouped displacements (linear combination of displacement vectors). They have the characteristic that each has the symmetry of an irreducible representation of the point group of the molecule.
The linear combination of displacements vectors that describe a normal mode transform among themselves as irreducible presentation of the point group of the molecule
We will not review how these irreducible representations are formed for each normal mode. We begin with the primitive Cartesians vectors on each atom. There are thus 3N vectors in the basis. This produced a 3N-dimensional (reducible, normally) representation of the group. We need that X3N for each group operation to use the reduction formula. Check out: https://sites.cns.utexas.edu/jones_c...odes-vibration
Water
Let’s begin with an example: H2O, which is a C2v molecule.
.png?revision=1)
Water belongs to the C2v symmetry group and has the following symmetry elements:
- \(\hat{E}\)
- \(\hat{C}_{2}(z)\)
- \(\hat{\rho}_{v}(x y)\)
- \(\hat{\rho}_{v^{\prime}}(y z)\)
Its character table is shown below.
\[ \begin{array}{|c|c|c|c|c|c|} \hline \text{C}_{2v} & \text{E} & \text{C}_2^z & \sigma_{xz} & \sigma_{yz} & \text{h = 4} \\ \hline \text{A}_1 & 1 & 1 & 1 & 1 & z,~ x^2,~y^2,~z^2 \\ \hline \text{A}_2 & 1 & 1 & -1 & -1 & \text{xy, R}_z \\ \hline \text{B}_1 & 1 & -1 & 1 & -1 & \text{x, xz, R}_y \\ \hline \text{B}_2 & 1 & -1 & -1 & 1 & \text{y, yz, R}_x \\ \hline \Gamma_{tot} & -9 & -1 & 1 & 3 \\ \hline \end{array} \nonumber \]
The Cartesian vectors form the basis of a 9-dimensional representation (three dimensions on each atom).
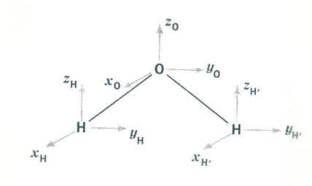
A symmetry analysis for water begins by determining how these 9 coordinates behave under the symmetry operations of the C2v group. You should be able to show that this generates the reducible representation \(Γ_{tot}\), which is given in the last row of the character table shown above. \(Γ_{tot}\) can also be calculated as
\[Γ_{uma} (Γ_x + Γ_y + Γ_z), \nonumber \]
where \(Γ_{uma}\) is the behavior of the atoms under the symmetry operations of the group. Of the 9 degrees of freedom possessed by the water molecule, three are for translation of the center of mass in the x-, y- and z-directions, and three are related to rotation about the x-, y-, and z-axes. This leaves three vibrational degrees of freedom. To determine the symmetry of the vibrational modes we decompose \(Γ_{tot}\) into the unit vectors or irreducible representations of the C2v character table. This involves taking the dot product of \(Γ_{tot}\) with each of the irreducible representations of the C2v symmetry.
\[ \begin{matrix} \Gamma_{tot} \text{A}_1 = \dfrac{[(9)(1) + (-1)(1) + (1)(1) + (3)(1)]}{4} = 3 \\ \Gamma_{tot} \text{A}_2 = \dfrac{[(9)(1) + (-1)(1) + (1)(-1) + (3)(-1)]}{4} = 1 \\ \Gamma_{tot} \text{B}_1 = \dfrac{[(9)(1) + (-1)(-1) + (1)(1) + (3)(-1)]}{4} = 2 \\ \Gamma_{tot} \text{B}_2 = \dfrac{[(9)(1) + (-1)(-1) + (1)(-1) + (3)(1)]}{4} = 3 \end{matrix} \nonumber \]
This procedure has revealed the that the reducible representation, \(Γ_{tot}\), is composed of the following irreducible representations:
\[ \Gamma_{tot} = 3 \text{A}_1 + \text{A}_2 + 2 \text{B}_1 + 3 \text{B}_2 \nonumber \]
From the right side of the character table we see that translation and rotation have the following symmetry properties:
\[ \begin{matrix} \Gamma_{trans} = \text{A}_1 + \text{B}_1 + \text{B}_2 \\ \Gamma_{rot} = \text{A}_2 + \text{B}_1 + \text{B}_2 \end{matrix} \nonumber \]
From this information we can determine the symmetry properties of the vibrational modes of the water molecule.
\[ \Gamma_{vib} = \Gamma_{tot} - \Gamma_{trans} - \Gamma_{rot} = 2 \text{A}_1 + \text{B}_2 \nonumber \]
There are three vibrational fundamentals. And, since there are two bonds there will be two stretching vibrations and one bending vibration. To determine which symmetry classification the bend belongs to, examine how the H-O-H bond angle transforms under the symmetry operations of the C2v group.
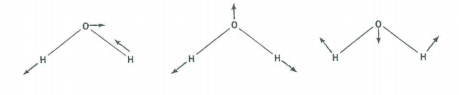
The vibrational modes are shown above. Convince yourself that their symmetry properties are captured in the table below.
\[ \begin{array}{|c|c|c|c|c|c|} \hline \text{C}_{2v} & \text{E} & \text{C}_2^z & \sigma_{xz} & \sigma_{yz} \\ \hline \Gamma_{bend} & 1 & 1 & 1 & 1 & \text{A}_1 \\ \hline \Gamma_{stretch} & 1 & 1 & 1 & 1 & \text{A}_1 \\ \hline \Gamma_{stretch} & 1 & -1 & -1 & 1 & \text{B}_2 \\ \hline \end{array} \nonumber \]
Therefore, the stretches have \(A_1\) symmetry and the bend has \(B_2\) symmetry.
Predict three vibrational normal modes, \(2a_1+b_2\). The two totally symmetric normal coordinates are linear combinations of symmetric stretch and bend (https://people.chem.ucsb.edu/laverma...water_vib.html).
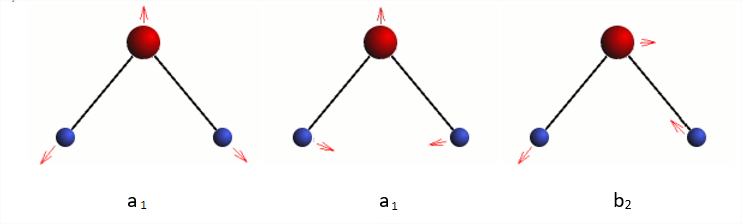
One of the two \(a_1\) modes is mostly the stretch (high frequency), while the other is mostly the bend (lower frequency). The \(b_2\) is the unsymmetrical stretch.
Other Molecules
Determination of normal modes becomes quite complex as the number of atoms in the molecule increases. Nowadays, computer programs that simulate molecular vibrations can be used to perform these calculations.
The example of [PtCl4]2- shows the increasing complexity. The molecule has five atoms and therefore 15 degrees of freedom, 9 of these are vibrational degrees of freedom. The nine normal modes are exemplified below along with the irreducible representation the normal mode belongs to (D4h point group).
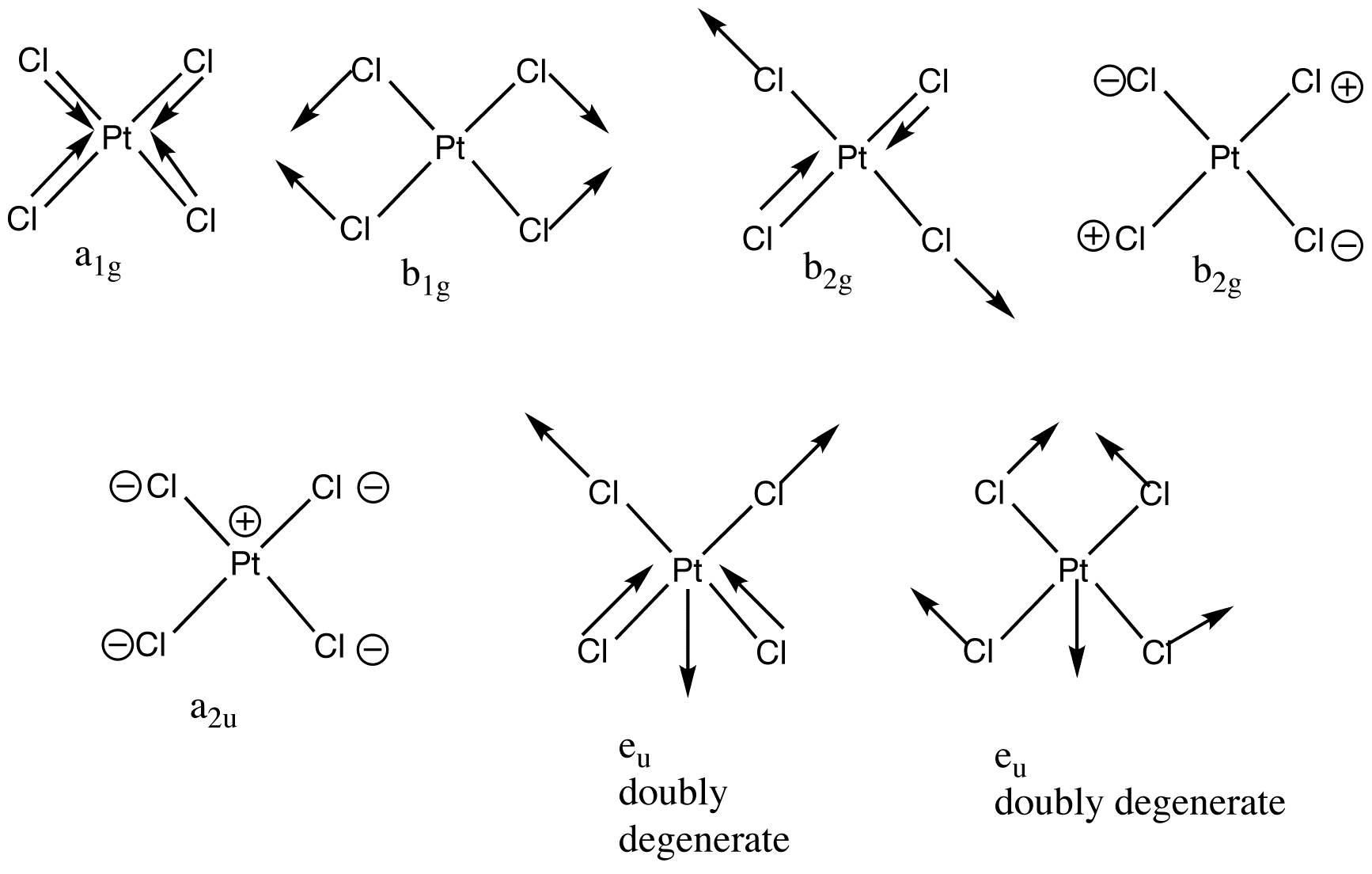
A1g, b1g and eu are stretching vibrations whereas b2g, a2u, b2u and eu are bending vibrations.

