3.4: Resonant Raman Spectroscopy
- Page ID
- 366529
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)In the previous discussion of Raman spectroscopy, the incident laser wavelength is not in resonance with the electronic transition, hence it is often referred to as non-resonant Raman scattering like below.

If \(\nu_o\) is tuned close to \(\nu_{el}\), the frequency of an electronic transition, normal modes that are vibronically active in the electronic transition are intensified in the Raman scattering. This is called the resonance Raman effect, because \(\nu_{o}\) comes close to being in resonance with \(\nu_{el}\). Because the laser photon can be absorbed by a real electronic state, and not a virtual state, the interaction of photons with vibrational is enhanced and there is a greater probability of the molecule being vibrationally excited after scattering. If the absorption is electronically allowed, mostly totally symmetric modes appear in the Raman spectrum.
Advantages
- Intensity is enhanced – allows measurements of dilute samples (i.e., metal centers of metalloproteins)
- Spectrum is simplified. Only a few vibrations are enhanced. Selects only vibrations that are associated with absorbing chromophores (or specifically the electronic transition).
- Long progression of a vibration are the often observed enabling the vibrational potential energy to be specified over large range of \(\nu\). This enables a greater description of the vibrational potential energy surfaces for the probe molecule.

Disadvantage
- Local heating that perturbs the sample during Raman Probing!
- Also fluorescence can obscure signals
Inducing a Dipole via the Polarizability Tensor (simple math)
The simple undergraduate description of polarizability, \(α\), is that it is a scalar whose amplitude describes the amplitude of the induced dipole moment on a molecule via an applied electric field, which is a vector oriented along its polarization (presuming linear polarization here). Hence:
\[\bar{\mu}_{i n d}=\alpha \bar{E} \nonumber \]
And the amplitude of the induced dipole moment is oriented directly along the same orientation as the polarization of the applied electric field. However, α is not really a scalar, but is a 2-rank tensor (matrix) consisting of nine elements:
\[\alpha=\left|\begin{array}{ccc}
\alpha_{x x} & \alpha_{x y} & \alpha_{x z} \\
\alpha_{y x} & \alpha_{y y} & \alpha_{y x} \\
\alpha_{z x} & \alpha_{x x} & \alpha_{z z}
\end{array}\right| \nonumber \]
Now a simplification, the tensor is symmetric (i.e., \(\alpha_{i j}=\alpha_{j i}\)), so there are only six independent elements. \(α\) can be separated into two tensors:
\[\left|\begin{array}{ccc}
\alpha_{x x} & \alpha_{x y} & \alpha_{x z} \\
\alpha_{y x} & \alpha_{y y} & \alpha_{y x} \\
\alpha_{z x} & \alpha_{z x} & \alpha_{z z}
\end{array}\right|=\left|\begin{array}{ccc}
\alpha_{x x} & 0 & 0 \\
0 & \alpha_{y y} & 0 \\
0 & 0 & \alpha_{z z}
\end{array}\right|+\left|\begin{array}{ccc}
0 & \alpha_{x y} & \alpha_{x z} \\
\alpha_{y x} & 0 & \alpha_{y x} \\
\alpha_{x} & \alpha_{z x} & 0
\end{array}\right| \nonumber \]
The first matrix is the isotropic contribution to α and the second is the anisotropic. Using vectors along the X, Y and Z axis you can confirm that using only the isotropic component of \(α\) the induced dipole moment, \(\vec{\mu}_{Pind}\), will be oriented only along the direction of \(\vec{E}\). The off-diagonal elements of \(α\) induce a dipole moment in one direction when the applied electric field it oriented in a normal orientation. Hence the term anisotropic to describe this component.
Polarization of Raman Bands
If a symmetric molecule with isotropic polarizability (i.e. no off axis non-zero elements) is irradiated by a polarized laser radiation along y, and the molecule is observed along x, we will observe z polarized Raleigh scattering only.
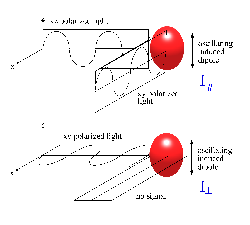
If \(α\) is not isotropic, induced dipole will have a component along y, and the scattering radiation is then partially or completely depolarized. Generally, \(α\) is not isotropic and some depolarization is observed. In Stokes Raman scattering, the polarization depends on the symmetry of the excited vibration. The following rules have been developed:
For liquid samples:
- Even if \(α\) is isotropic, for a totally symmetric (e..g \(A_g\)) normal mode, the Raman scattered light is polarized.
- For a non-totally symmetric normal mode, the scattered light is depolarized and we can construct a depolarization ratio:
\[\rho=\frac{I_{y}(\perp)}{I_{x}(\square)} \nonumber \]
Depolarized means \(ρ=3/4\) (non-symmetric) and polarized mean \(0<=ρ <= ¾\) (only for totally symmetric modes).

Below, we show the effect for the totally symmetric \(v_1\) mode of the \(\ce{ClO4^{–}}\) ion. The figure shows the spectra obtained using both vertically polarized and horizontally polarized light. The large \(v_1\) peak near 1000 cm–1 cannot be observed when the beam is horizontally polarized. The very small amount of scattered light observed at this wavelength in the horizontally polarized spectrum results from imperfect polarization of the laser beam.
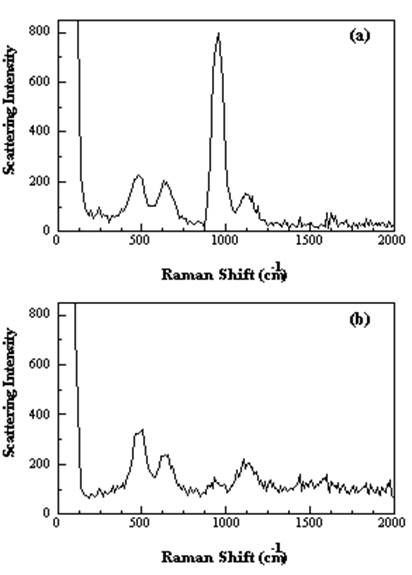
Figure 3. Raman spectra of a saturated solution of NaClO4 with (a) vertically and (b) horizontally polarized light impinged on the sample. https://www.thevespiary.org/library/...10mW.Diode.pdf

