3.3: Raman vs. IR Spectroscopies
- Page ID
- 366526
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)IR spectra
The vibrations of molecules can either be detected by direct absorption, which requires that the change in the dipole moment with normal coordinate be not equal to zero.
\[\left(\frac{d \mu}{d q}\right)_{q_{e q}} \neq 0 \nonumber \]
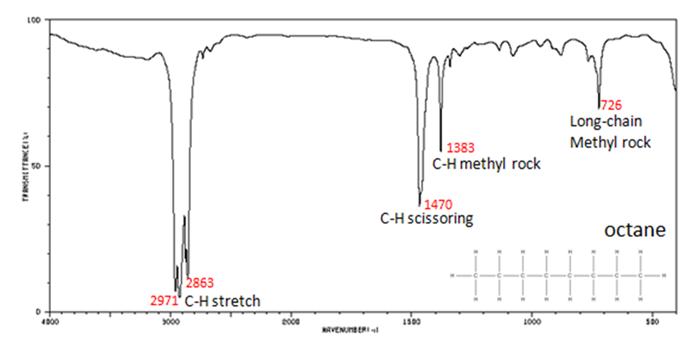
Infrared Spectrum of Octane
Raman
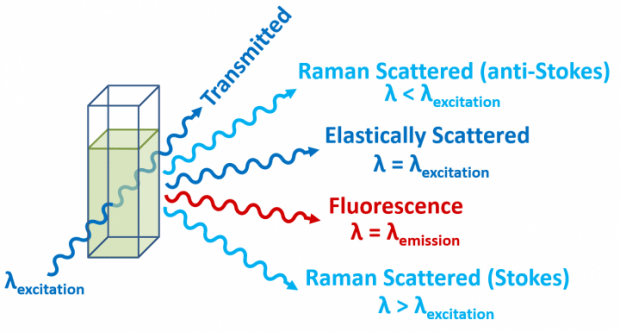
Or it can be detection by the Raman effect, which is the inelastic scattering of a high energy (visible or UV) photon. Vibrational frequencies can also be obtains by single level fluorescence (like vibronic features in the absorption spectrum).
_(2019)_1662-1683.png?revision=1&size=bestfit&width=417&height=641)
Schematic of one possible dispersive Raman spectroscopy setup. (CC BY-SA 4.0; Toommm via Wikipedia)

Energy-level diagram showing the states involved in Raman spectra. CC BY-SA 3.0; Moxfyre, via Wikipedia).
Energy level diagram showing the states involved in Raman signal. The line thickness is roughly proportional to the signal strength from the different transitions.
Requirement for Raman transition to be observed
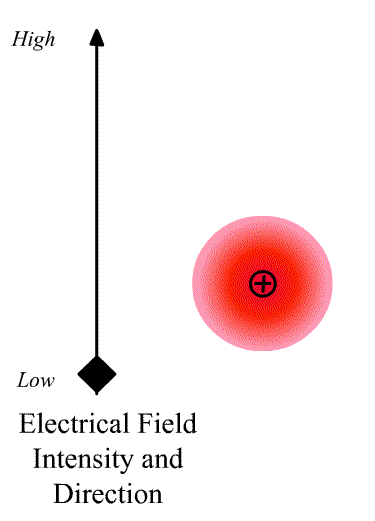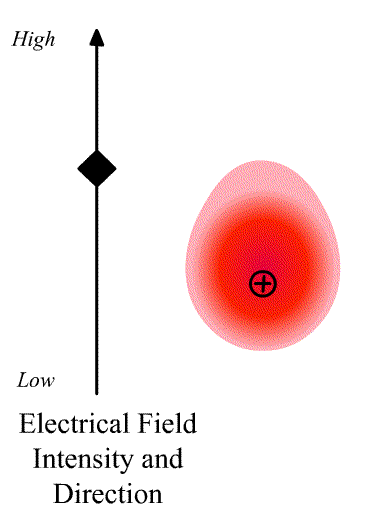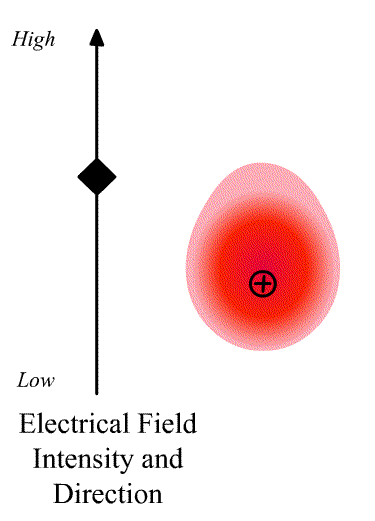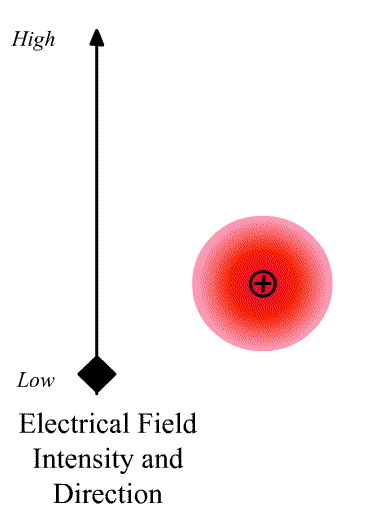
The intensity of the light scatter from a molecule depends upon the size of the induced dipole moment, which depends on the oscillating electric fiends, E of the radiation and the polarizability α. We can write
\[\vec{D}=\alpha\vec{E} \nonumber \]
where \(\vec{D}\) is a vector and \(\alpha\) is the polarizability tensor whose elements depends on the molecule (specifically the symmetry of the molecule).
The polarizability tensor is defined:
\[\alpha=\left[\begin{array}{lll}
\alpha_{x x} & \alpha_{x y} & \alpha_{x z} \\
\alpha_{y x} & \alpha_{y y} & \alpha_{y z} \\
\alpha_{z x} & \alpha_{z y} & \alpha_{z z}
\end{array}\right] \nonumber \]
The elements describing the response parallel to the applied electric field are those along the diagonal. A large value of {\displaystyle \alpha _{yx}}{\displaystyle \alpha _{yx}} here means that an electric-field applied in the {\displaystyle x}x-direction would strongly polarize the material in the {\displaystyle y}y-direction. Explicit expressions for {\displaystyle \alpha }\alpha have been given for homogeneous anisotropic ellipsoidal bodies.
\(\vec{D}\) is responsible for the Raleigh Scattering, which is the elastic scattering of the same frequency as the incident radiation. Raman (inelastic) scattering will occur at:
\[\nu-\nu_{0} \nonumber \]
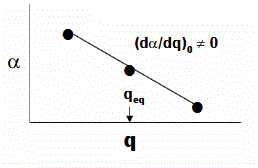
Where \(\nu_o\) is the frequency of the normal mode \(q_o\). If there is a change in the polarizability of the molecule for a small displacement around equilibrium (\(q_{eq}\)) with respect to the normal mode coordinate (\(q\)).
\[\alpha=\alpha_{0}+\left(\frac{\partial \alpha}{\partial q}\right)_{0} q+\ldots \nonumber \]
where
- \(\alpha_{0}\) is the polarizability at the equilibrium position and
- \(\left(\frac{\partial \alpha}{\partial q}\right)_{0}\) is the rate of change of the polarization wrt the coordinate evaluated at the equilibrium position
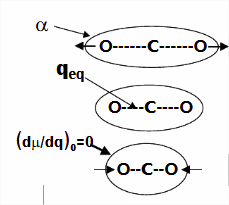
The Raman activity and Raman intensity of a particular normal mode are determined from the polarizability tensors for that mode, whereas infrared activity/intensity are determined from dipole moment tensors. These relationships are shown diagrammatically below, where \(\alpha\) is the polarizability, \(\mu\) is the dipole moment, and q is the motional coordinate associated with a particular normal mode. Note that the intensity, \(I\) of the transition, is proportional to:
- \((d\alpha / dq)_0\) for Raman
- and \((d\mu / dq)_0\) and infrared activity.
The zero subscript indicates that the derivative is evaluated at the equilibrium (ground state) condition of the motional coordinate.
Carbon Dioxide
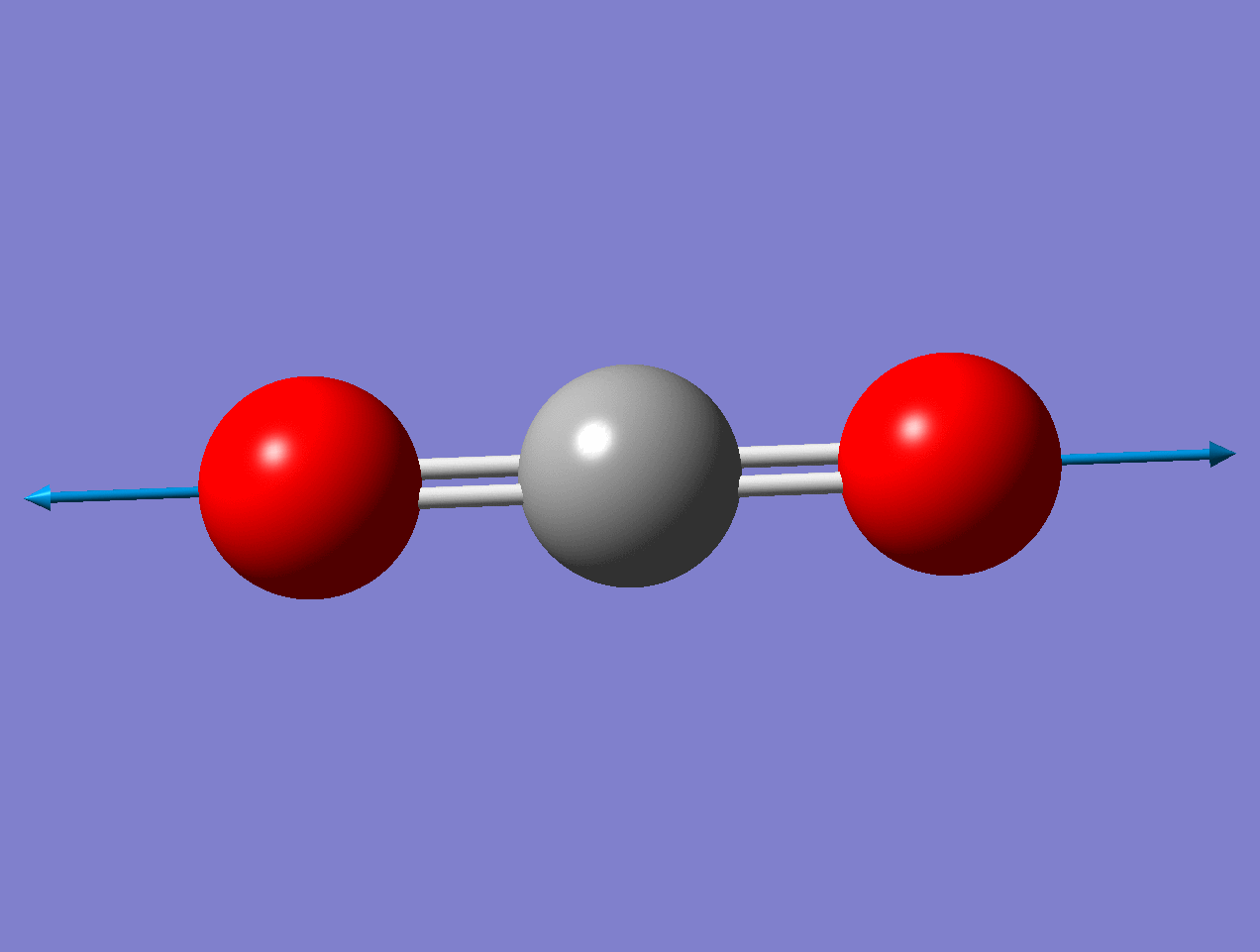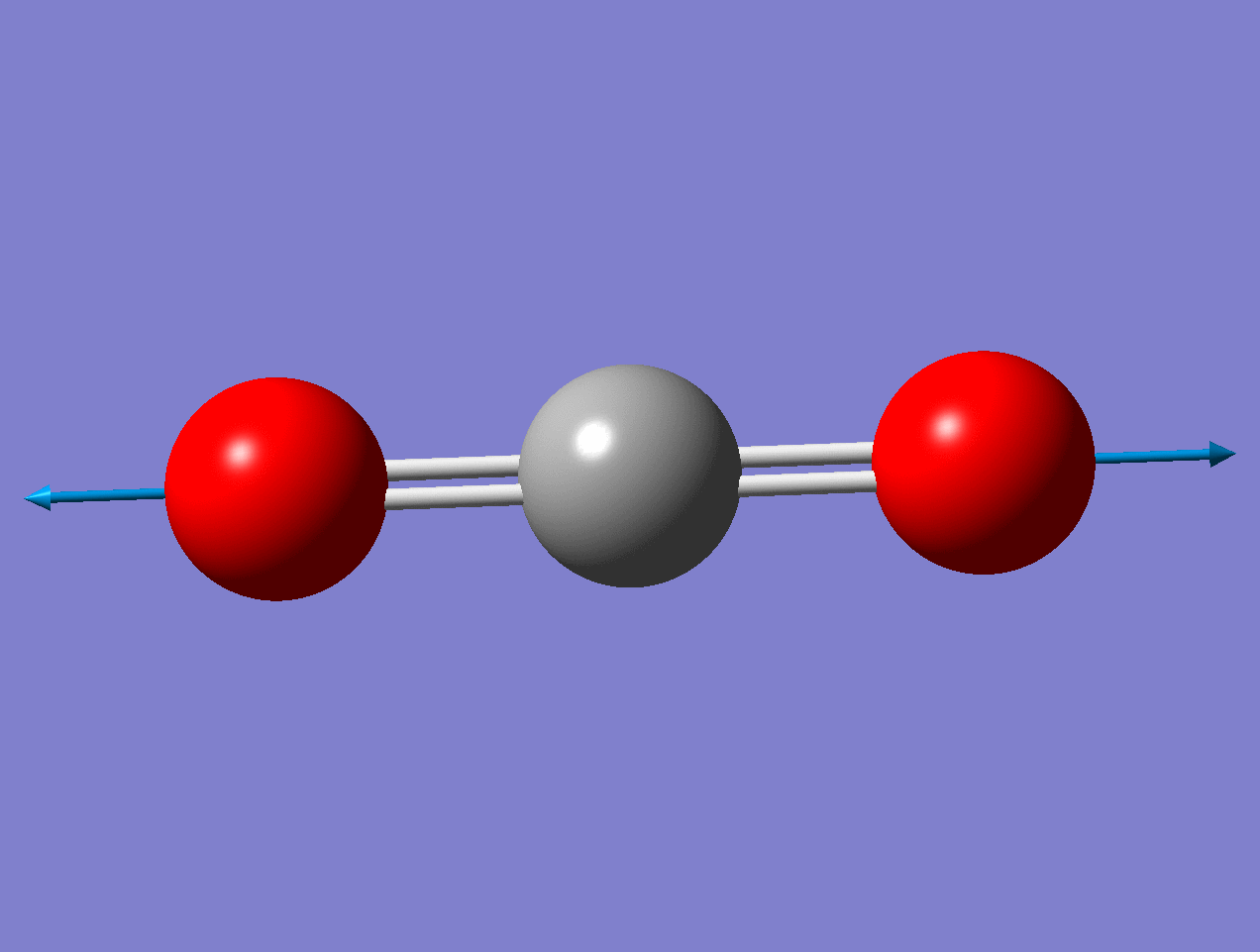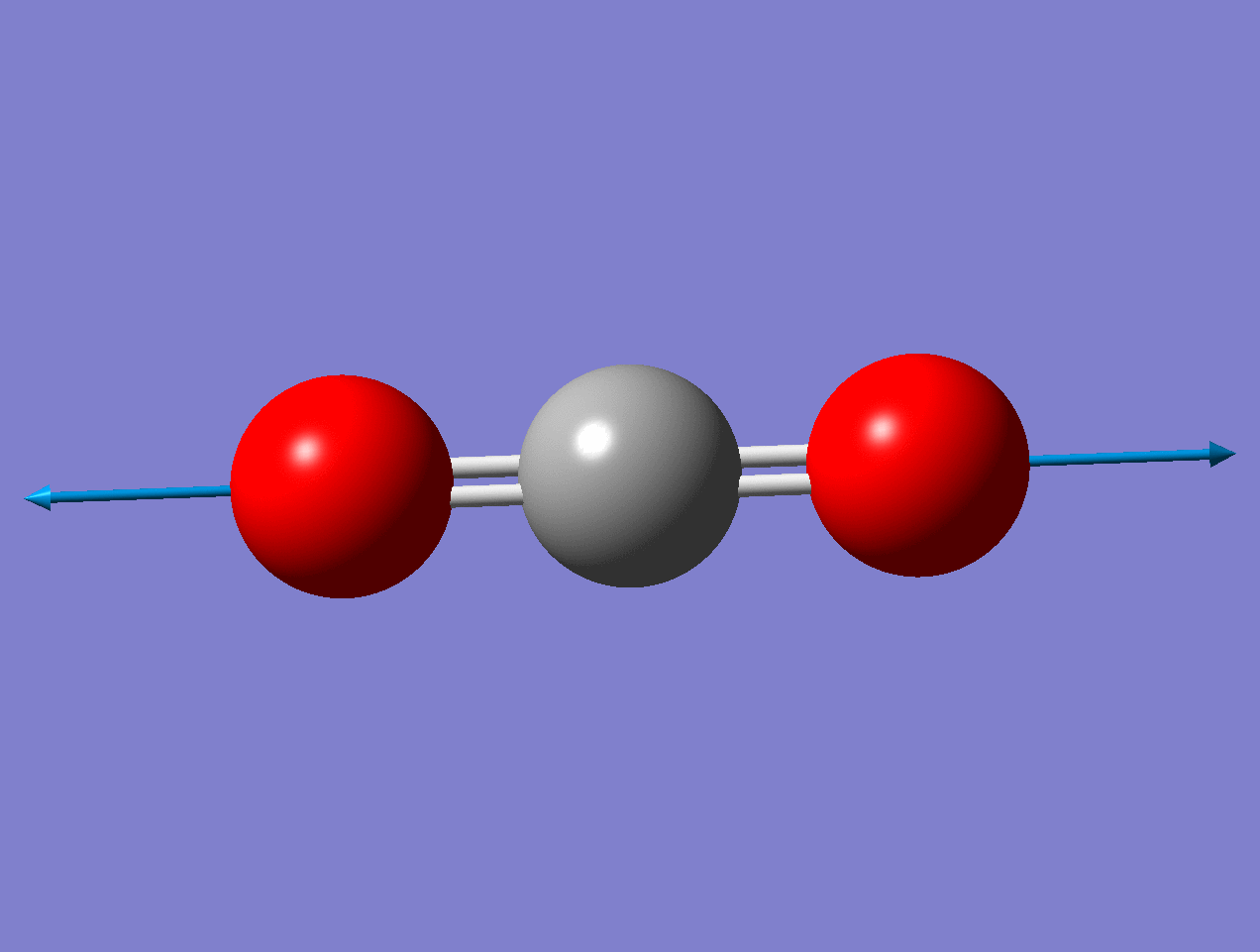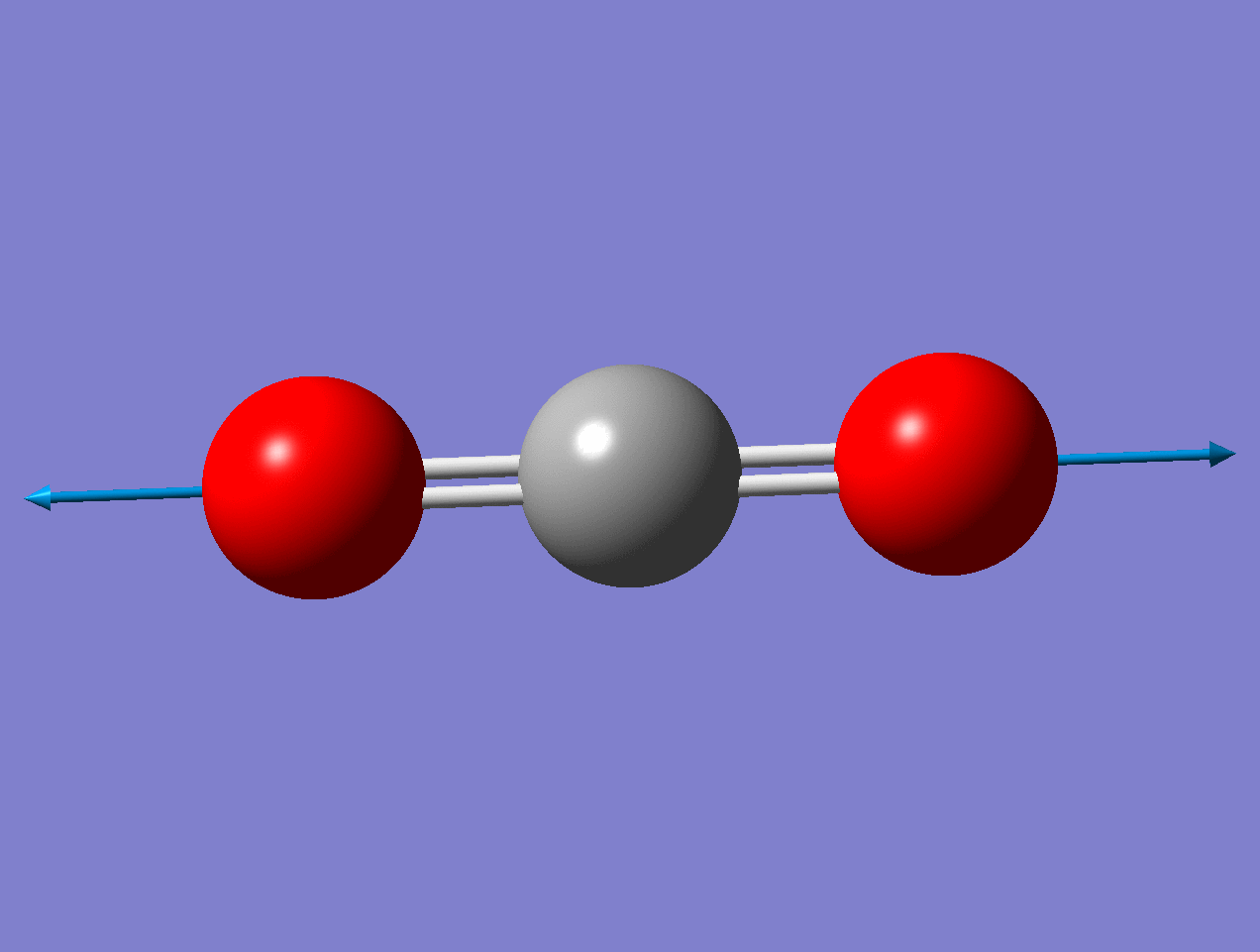
Using the carbon dioxide molecule (a molecule with a center of inversion) as an example, the diagrams below show that the symmetric stretching mode of \(CO_2\) has a non-zero \(d\alpha / dq)_0\) but a zero value for \(d\mu / dq)_0\), while the antisymmetric stretching mode has a non-zero \(d\mu / dq\) but a zero value for \((d\alpha / dq)_0\).
For the symmetric stretch in \(\ce{CO2}\), the \(α\) increases along z axis.
https://imgur.com/gallery/vnmaBrJ
As the mode vibrates, the electron cloud changes and the polarization changes

This a Raman Active mode since
\[\left(\frac{\partial \alpha}{\partial q}\right)_{0} \neq 0 \nonumber \]
This a IR Inactive mode since
The dipole moment of the molecule does not change during the vibration due to symmetry.
\[\left(\dfrac{d\mu}{dq} \right)_o = 0 \nonumber \]
For the asymmetric stretch in \(\ce{CO2}\), there is no change in \(α_{zz}\) (or any other components) for small displacements.
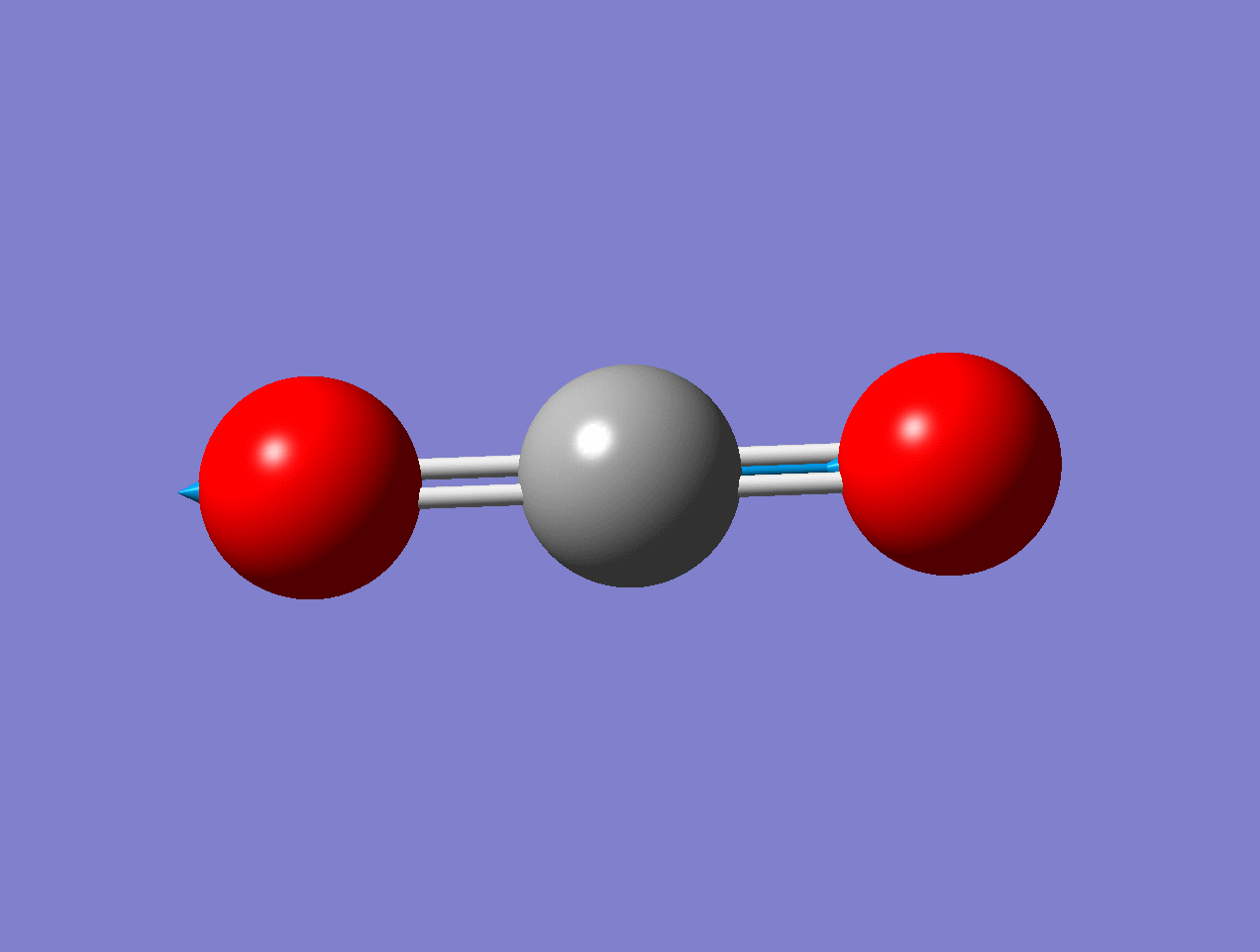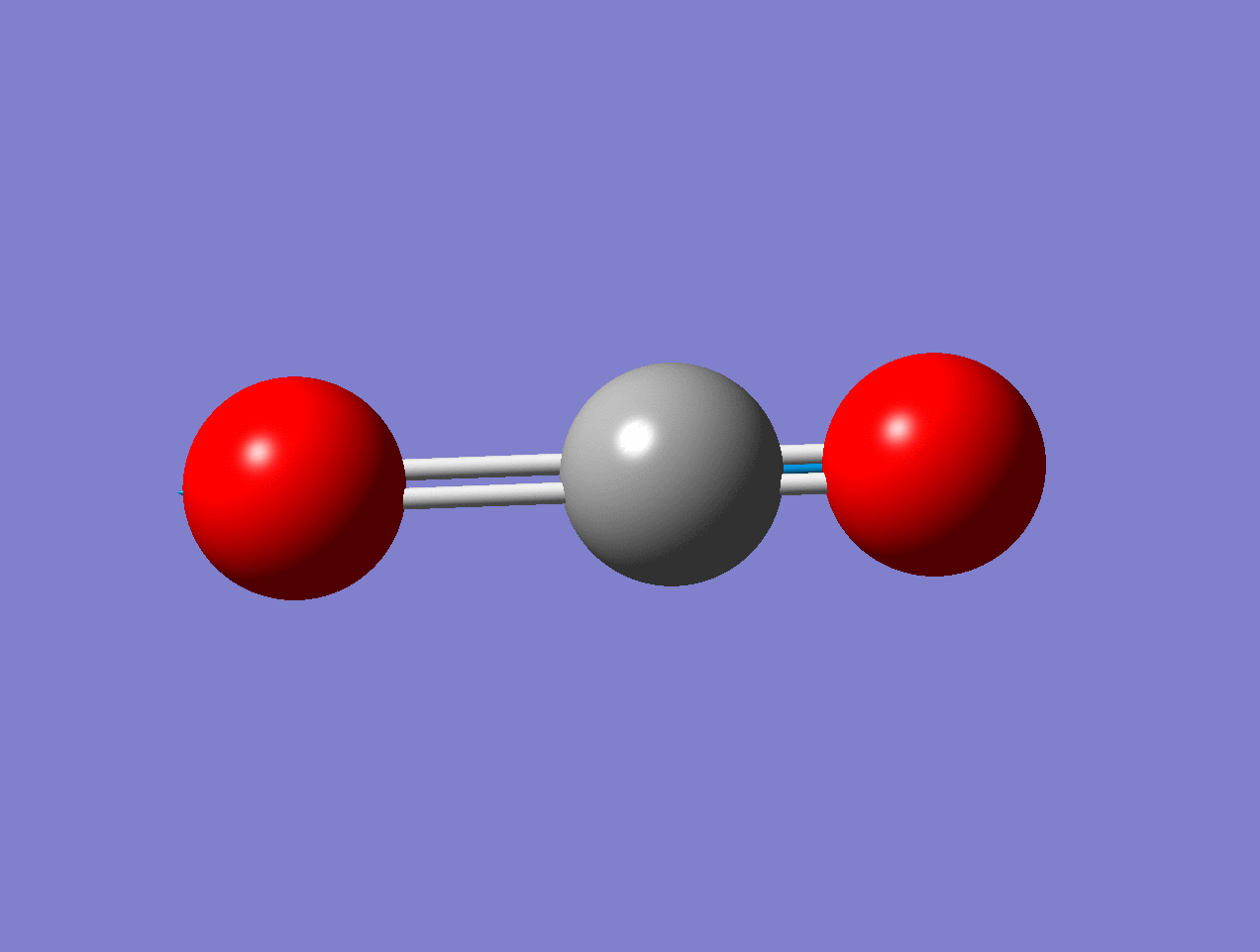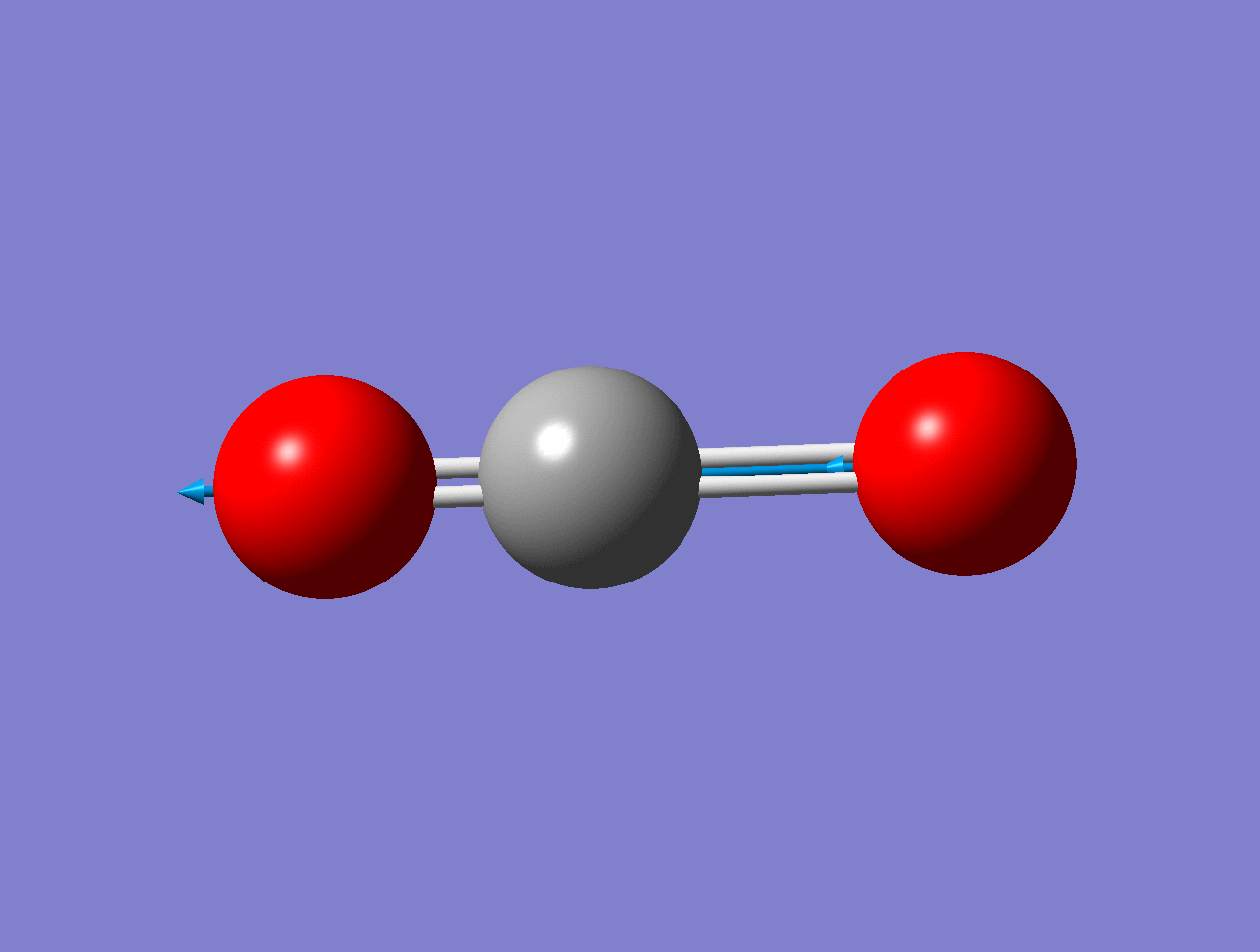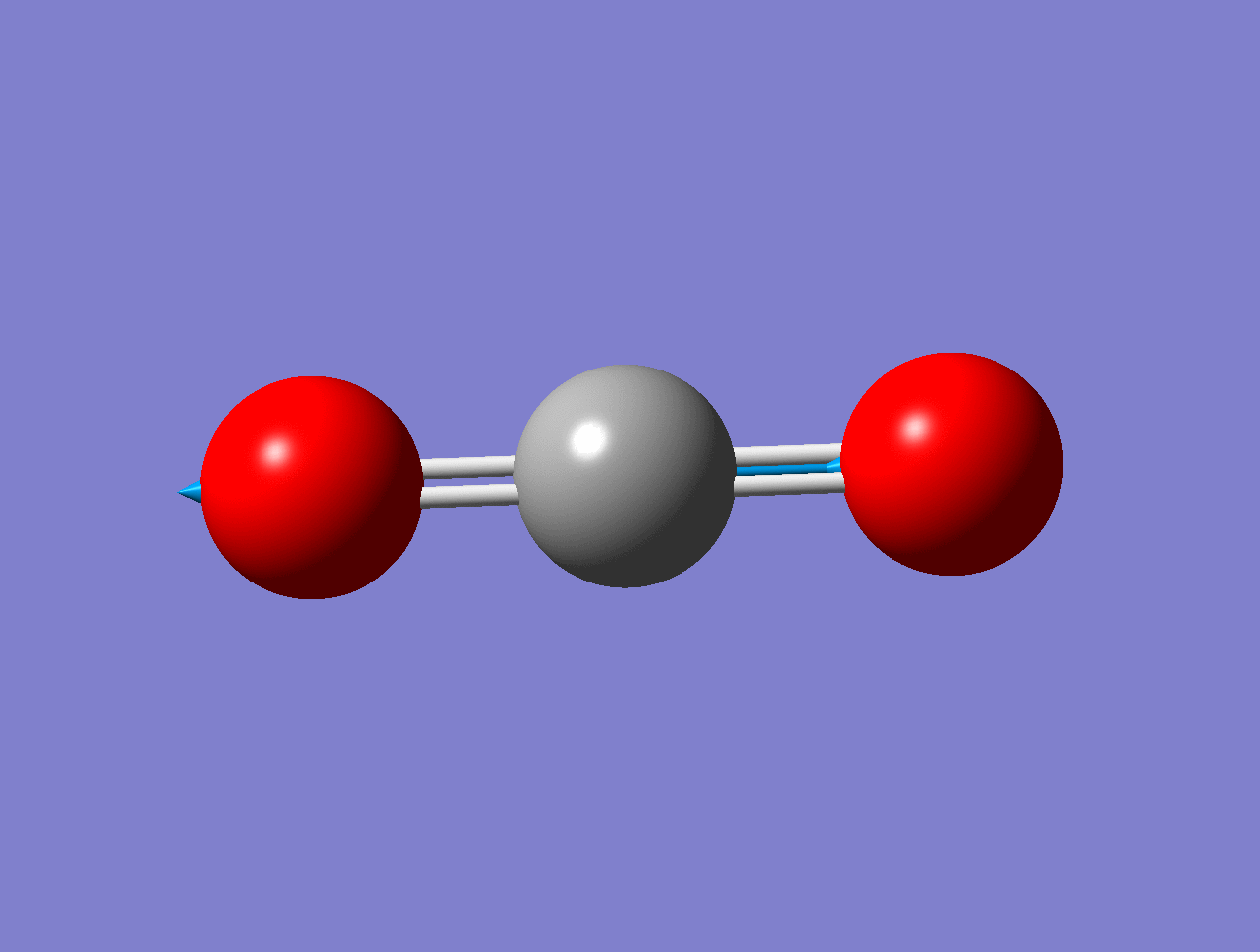
As the mode vibrates, the electron cloud changes and the polarization changes and the dipole moment.

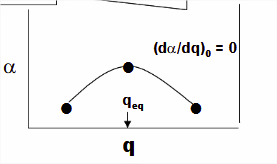
Raman Inactive
This a Raman Inactive mode since
\[\left(\frac{\partial \alpha}{\partial q}\right)_{0} = 0 \nonumber \]
This a Raman Active mode since
The dipole moment of the molecule does not change during the vibration due to symmetry.
\[\left(\dfrac{d\mu}{dq} \right)_o \neq 0 \nonumber \]
In the actual spectra of \(\ce{CO2}\), the symmetric stretch appears in the Raman spectrum but not in the infrared spectrum, and the antisymmetric stretch appears in the infrared but not the Raman. In a qualitative sense one can see that the polarizability ellipsoids in the stretched and compressed states of the symmetric stretch are not equivalent (in shape and volume), whereas they are for the antisymmetric stretch.
Comparison
We will see later how group theory helps us to decide about which transitions are IR active with
\[\left(\frac{d \mu}{d q}\right)_{q_{e q}} \neq 0 \nonumber \]
and which are Raman active with
\[\left(\frac{d \alpha}{d q}\right)_{q_{e q}} \neq 0 \nonumber \]
Unfortunately, a transition in a particular mode may be “Active" from a symmetry point of view, but the actual change in \(α\) or \(μ\) may be so small that the transition may not be observed. In IR and Raman, we often do not see all the predicted active vibrations.

