3.2: Polyatomic Molecules
- Page ID
- 366525
These have many more ways to vibrate (vibrational degrees of freedom) than a diatomic that had only one. Each bond can vibrate (stretch), and each pair of bonds attached to a common atom can bend. These motions are all described by their individual force constants., but these individual bonds stretches and bends are all coupled together so that all atoms vibration together in converted set of frequencies, call the normal modes frequencies. These group vibrations themselves are called normal modes. The normal modes and the force constants are not easy to find, but require a procedure called normal mode analysis.
Details behind normal mode analysis are beyond what we have time to develop in this course. Anyone who wants to really learn the mathematics behind this method should consult the classical textbook by Wilson, Decius and Corss, “Molecular Vibrations” or look at chapter 6 in Drago.
The gist is as follows: If we have a diatomic molecule, we can solve the force constant since we can measure the vibrations frequency and calculate the reduced mass, knowing the masses of the atoms. This is a principle problem which becomes more complicated in a polyatomic molecule. We must task first, how many Normal Modes are there? These normal modes are linear combinations of the possible Cartesian displacement of each atoms.
| Symmetric Stretching | Asymmetric Stretching | Wagging |
|---|---|---|
 |
 |
 |
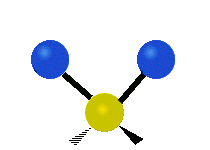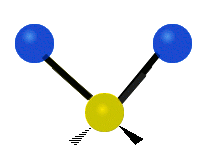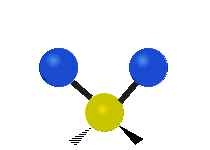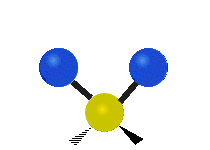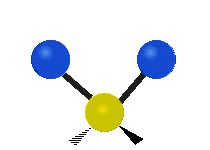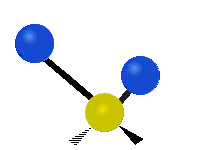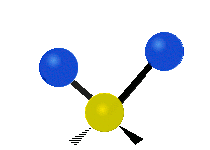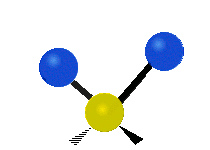| Twisting | Scissoring | Rocking |
 |
 |
 |
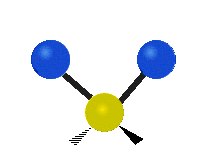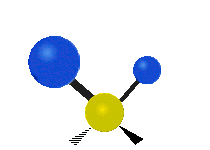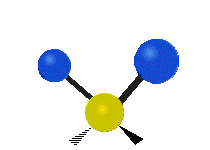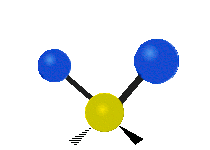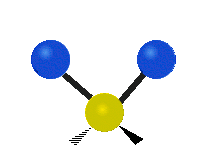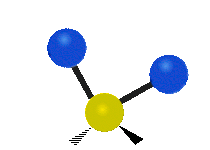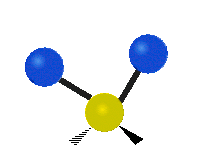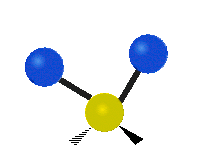Figure \(\PageIndex{1}\): Six types of Vibrational Modes. Images used with permission (Public Domain; Tiago Becerra Paolini).
Calculate Number of Vibrational Modes
Degree of freedom is the number of variables required to describe the motion of a particle completely. For an atom moving in 3-dimensional space, three coordinates are adequate so its degree of freedom is three. Its motion is purely translational. If we have a molecule made of N atoms (or ions), the degree of freedom becomes 3N, because each atom has 3 degrees of freedom. Furthermore, since these atoms are bonded together, all motions are not translational; some become rotational, some others vibration. For non-linear molecules, all rotational motions can be described in terms of rotations around 3 axes, the rotational degree of freedom is 3 and the remaining 3N-6 degrees of freedom constitute vibrational motion. For a linear molecule however, rotation around its own axis is no rotation because it leave the molecule unchanged. So there are only 2 rotational degrees of freedom for any linear molecule leaving 3N-5 degrees of freedom for vibration.
The degrees of vibrational modes for linear molecules can be calculated using the formula:
\[3N-5 \label{1} \]
The degrees of freedom for nonlinear molecules can be calculated using the formula:
\[3N-6 \label{2} \]
\(n\) is equal to the number of atoms within the molecule of interest. The following procedure should be followed when trying to calculate the number of vibrational modes:
- Determine if the molecule is linear or nonlinear (i.e. Draw out molecule using VSEPR). If linear, use Equation \ref{1}. If nonlinear, use Equation \ref{2}
- Calculate how many atoms are in your molecule. This is your \(N\) value.
- Plug in your \(N\) value and solve.
Each of the normal modes must preserve the center of mass of the molecule, but not the bond lengths and angles. Each has a characteristic frequency that MAY be measured by IR or Raman spectroscopy. These are assumed to be known. There is a lot more involved in constructing Normal Modes, but we will ignore it for now in this class.
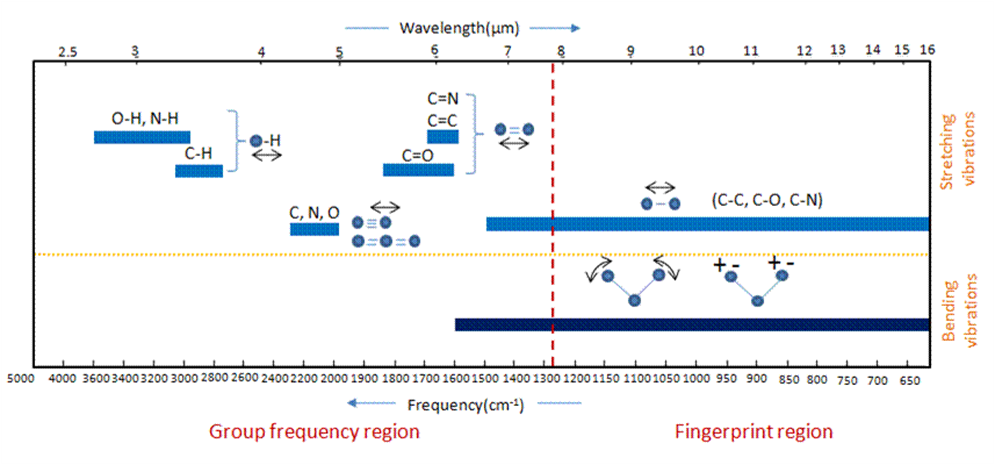
The region of the infrared spectrum from 1200 to 700 cm-1 is called the fingerprint region. This region is notable for the large number of infrared bands that are found there. Many different vibrations, including C-O, C-C and C-N single bond stretches, C-H bending vibrations, and some bands due to benzene rings are found in this region. The fingerprint region is often the most complex and confusing region to interpret, and is usually the last section of a spectrum to be interpreted. However, the utility of the fingerprint region is that the many bands there provide a fingerprint for a molecule.
Local vs. Normal modes
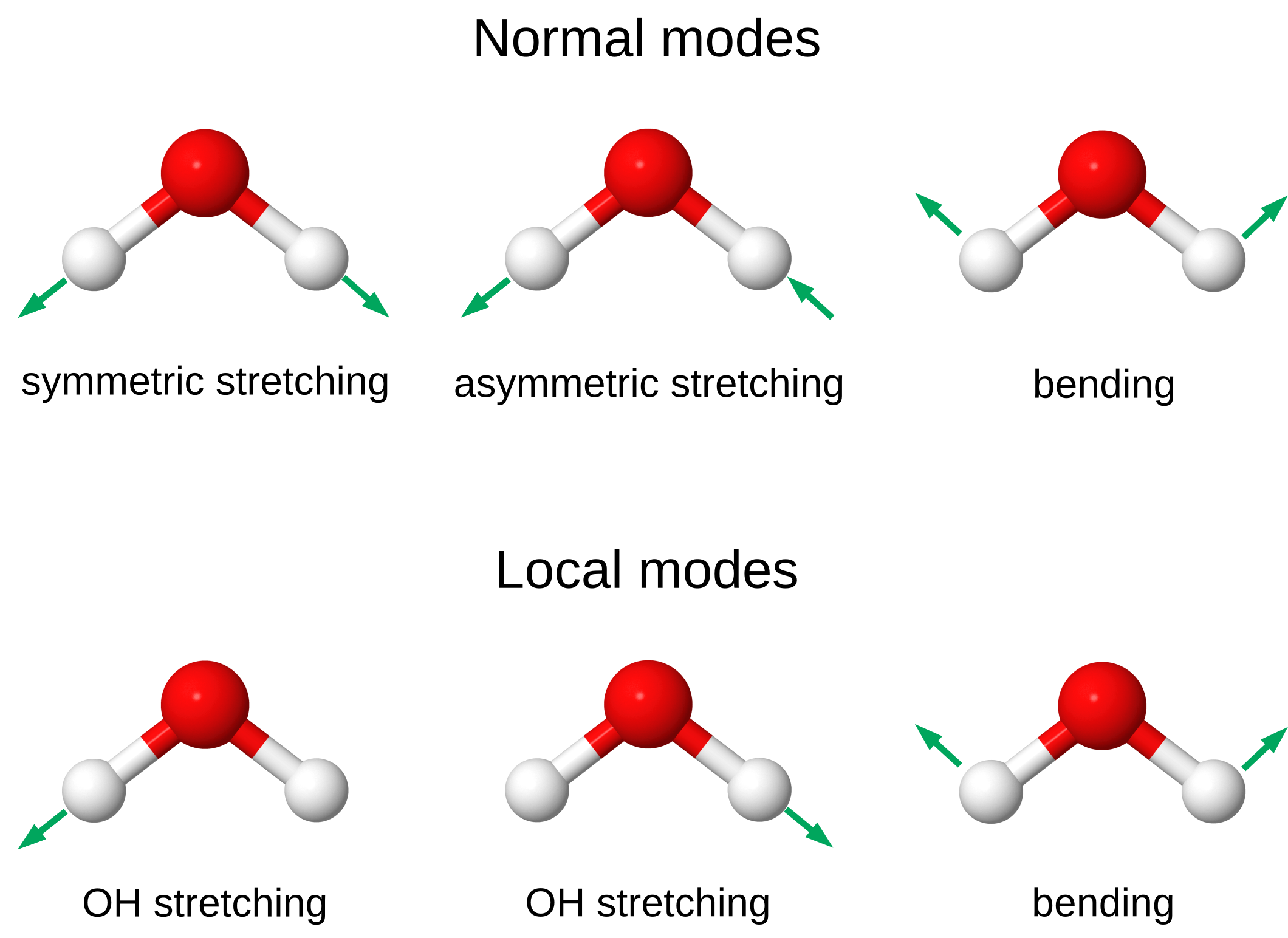
A useful tool for understanding vibrations is the concept of normal modes. These are patterns of vibration such that all components of a system move synchronously and with the same frequency, even if they do so in different directions. If a molecule is vibrating in a normal mode, its vibrational dynamics are straightforward: it continues to vibrate in the same pattern. More interesting is the situation where a polyatomic molecule vibrates in a pattern that is not a normal mode, e.g., when the vibration is localized on specific atomic positions or chemical bonds. These patterns are referred to as local modes, and their evolution in time is more challenging to predict and analyze.
- Water has three vibrational normal modes: the symmetric and asymmetric stretching modes, and a bending mode (below).
- These normal modes can be transformed to three local modes: two stretching modes describing the vibrations of the single OH bonds, and a bending mode.
https://strawberryfields.ai/photonic..._dynamics.html
The idea of group vibrations has a certain usefulness attached to it – information about vibrational motions of a molecule can sometimes be obtained without having to resort to a full blown normal mode analysis. Can we pick a vibrational frequency out of a spectrum and assign it to a particular functional group e.g. CH3-H, or CH2=0 or -C=-H?
Often we can, and this is the basis for the IR analytical method of identifying substance and the present of functional group in molecules. An IR band is usually found near 1700 cm-1 in a molecule with a --C=0 group, that is assigned to the stretching vibration. But it varies by quite a bit, depending on the other features of the molecules (-+ 150 cm-1).
If a particular group vibration involves largely a H, then deuteration will reduce the frequency of ~sqrt(2) confirming that the H is strongly involved. A good example of the interaction of group vibrations is the linear triatomic HCN. The displacement coordinate for the stretching are:
The individual force constants, F11 and F22 are such that the group frequencies are similar in the absence of coupling. In the absence of coupling, for L11, imaging H and a rigid C=-N moving like a diatomic and for L22 imagine a rigid H-C and a N moving like a diatomic. The symmetry of these vibrations are the same, so they can interact. Since the frequencies are similar, their interaction can be considerable.
For HCN, the two stretching frequencies are found at 3313 and 2089 cm-1. For deuterated (D-CN), these are lower to 2629 cm-1 and 1906 cm-1. If the 3313 cm-1 mode were a pure CH mode, it would have been reduced by sqrt(2) to 2360 cm-1; not quite as expected. But what of the 2089 cm-1 which could have been assigned as a “pure” CN stretch. It should have been reduced by only a minor factor about 2% (via reduced mass arguments). Actually, it was reduce by a factor of 1.1. This shows that the HC and the C-=N stretching vibrations are coupled in the normal modes and that the group vibration description is oversimplified. Since the deuteration has a larger effect on the higher frequency mode than the lower frequency, it is clear that the former has a larger contribution of C-H.
Chloroform
In chloroform (CHCl3), the small peak at 3019 cm–1 has been assigned to the C–H stretching vibration. Below illustrates the isotope effect in this vibrational mode when hydrogen is replaced by deuterium. The heavier isotope lowers the frequency of the C–H stretching vibration, which is well-described by the diatomic approximation (a local mode). The small Raman peak that appears just below 1205 cm–1 in the chloroform spectrum is attributed to the n4 asymmetric-stretching vibration. This vibrational mode involves motion of the hydrogen atom and its vibrational frequency is also decreased as the result of deuterium substitution.
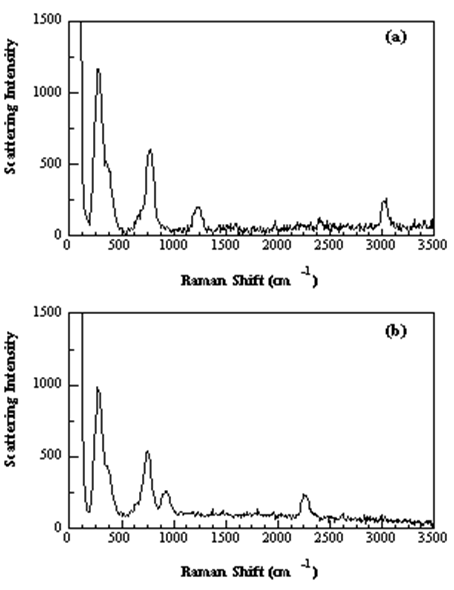
Figure 2. Raman spectra of neat chloroform (a) and deuterated chloroform (b).