3.1: Introduction to Vibrations

Last updated
Save as PDF

Page ID: 366524

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

We will begin with the vibrations of molecules since these are what we observed using IR and Raman spectroscopies. The vibrations of molecules can be modified by considering the atom as point mass that are attached to each other by massless springs (The electron pair bands). Thus for a simple diatomic molecules, we have only one vibration possible. The potential energy vs. internuclear distance, \(r\), can be represented by a Morse curve (as discussed earlier).

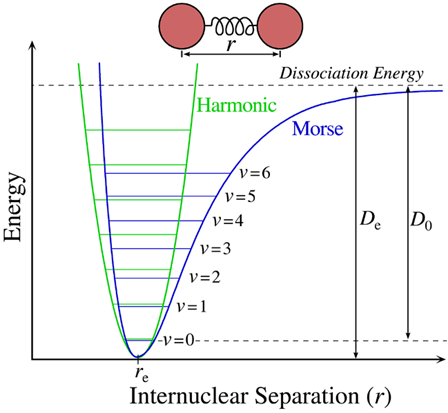
The Hooks law potential on the other hand is based on the ideal spring

\[F=-k x \nonumber \]

with \(x\) as the displacement from equilibrium (\(x=r-r_{eq}\)). This leads to the harmonic oscillator or Hooks’s law parabolic curve (green curve above) when integrating the definitions of the potential

\[F(x)=-\frac{d V(x)}{d x} \nonumber \]

in one dimensional space. This integration results in

\[V(r)=\frac{1}{2} k\left(r-r_{e q}\right)^2 \nonumber \]

The Harmonic and Morse potentials resemble each other for small displacements (\(x\)) from equilibrium. Solving the Schrödinger equation for the Harmonic Oscillator potentials results in the energy levels going as

\[E_{v}=\left(v+\frac{1}{2}\right) h \nu_{e} \nonumber \]

with \(v=0,1,2,3… \infty\) and

\[\nu_{e}=\frac{1}{2 \pi} \sqrt{\frac{k}{\mu}}. \nonumber \]

The Morse potential is an anharmonic potential that exhibits a more complicated expression for the vibrational energy levels.

\[E_{v}=h\left[\left(v+\frac{1}{2}\right) v_{e}-\left(v+\frac{1}{2}\right) \chi_{e} v_{e}\right]+\ldots \label{eq10} \]

plus other smaller terms.

The second term in Equation \ref{eq10} is the anharmonic coupling (deviations from the Harmonic Oscillator). The \(\chi_e\) term is a parameter that depends on details of \(V(r)\), \(D_e\) etc. Because of the 2nd term, the vibrational energy level spacing get closer together as \(v\) increases. For a Harmonic Oscillator, the spacings are equal.

Selection Rule for Vibrational Transitions

The vibrational molecule must interact with the oscillating electric field of the electromagnetic radiation, in order for a transition to take place. This means that there must be a change in the electric dipole moment for the particular transition. \[\left(\frac{d \mu}{d r}\right)_{r_{e q}} \neq 0 \nonumber \] The derivative of the mode with respect to the displacement must not equal zero.
\(Δv=+1\) (for absorption of radiation). This is rigorously true for a Harmonic Oscillator, but for any anharmonic oscillator (e.g. Morse Potential), then Δv=+2 (first overtone) transitions can occur. As well as the 2^nd overtone Δv=+3. The frequencies of the 1^st and 2^nd overtones provides information about the potential surface (i.e. χ_e can be determined.
For a diatomic, since \(μ\) is known, measurement of \(\nu_e\) provides a value for k, the force constant. \[k=\left(\frac{d^{2} V(r)}{d r^{2}}\right)_{r_{e q}} \nonumber \] The force constant is an important parameter, since it gives an indication of the strength of the bond.

Isotope Effects

Replacing of an atom with an isotope, had negligible effects on \(k\), but will affect \(μ\). The stretching vibrational of \(\ce{H-Cl}\) will be reduced by ~1.3 to 1.4 in frequency when H is substituted with D. This is because \(μ\) is increased by a factor of 2 and thus \(\nu_e\) is decreased by \(\sqrt{2}\).