3.7: Non-Fundamental Transations - Hot Bands, Combination Bands, and Fermi Resonances
- Page ID
- 366585
Hot bands
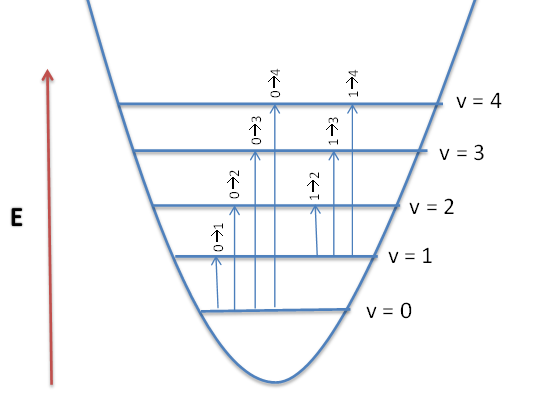
Hot bands are observed when an already excited vibration is further excited. For example an \(v_1\) to \(v_1'\) transition corresponds to a hot band in its IR spectrum. These transitions are temperature dependent, with lower signal intensity at lower temperature, and higher signal intensity at higher temperature. This is because at room temperature only the ground state is highly populated (kT ~ 200 cm-1), based on the Boltzmann distribution. The Boltzmann distribution states that if molecules in thermal equilibrium occupy two states of energy \(ε_j\) and \(ε_i\), the relative populations of molecules occupying these states will be,
\[ \large \dfrac{n_{j}}{n_{i}}=\dfrac{e^{-\varepsilon _{j}/RT}}{e^{-\varepsilon _{i}/RT}}=e^{-\Delta \varepsilon /RT} \nonumber \]
where \(k\) is the Boltzmann constant and \(T\) is the temperature in Kelvin.
In the harmonic oscillator model, hot bands are impossible to distinguished from fundamental transitions because the energy levels are equally spaced. Because the spacing between energy levels in the anharmonic oscillator decrease with increasing vibrational levels, the hot bands occur at lower frequencies than the fundamentals. Also, the transition moment integrals are slightly different since the ground state will not necessarily be totally symmetric since it is not in \(v=0\).
For a simple three vibration system, a hot band transition would look like this:
\[ \psi ^{_{1}} \left( 0 \right )\psi ^{_{2}}\left ( 0 \right )\psi ^{_{3}}\left ( 1 \right )\rightarrow \psi ^{_{1}}\left ( 0 \right )\psi ^{_{2}}\left ( 0 \right )\psi ^{_{3}}\left ( 2 \right ) \nonumber \]
Combination Bands
It frequently occurs that particular fundamental may not occur for symmetry reason (above) , but it can be excited in combinations with a different normal mode, because the doubly excited state has a symmetry that is allowed by IR (or Raman) selection rules. This shares some similarity to vibronic coupling in electronic transitions.
For a simple three vibration system, A combination transition would look like this:
\[ \psi ^{_{1}} \left( 0 \right )\psi ^{_{2}}\left ( 0 \right )\psi ^{_{3}}\left ( 0 \right )\rightarrow \psi ^{_{1}}\left ( 1 \right )\psi ^{_{2}}\left ( 1 \right )\psi ^{_{3}}\left ( 0\right ) \nonumber \]
The thing to keep in mind is that a doubly vibrationally excited state normal modes \(q_1\) and \(q_2\) have a wavefunction with symmetry
\[\Gamma_{q_{1}} \otimes \Gamma_{q_{2}}. \nonumber \]
BF3 is of symmetry D3h (see https://people.chem.ucsb.edu/laverma...e/BF3_vib.html).
- The symmetric stretch, \(ν_1\), is of symmetry A1’ and is IR inactive (x, y transform a E’, while z transforms as A2”).
- The \(ν_2\) vibration of symmetry A2” and double degenerate E’ vibrations ν3 (ν4).
A combination band is formed at frequency ν1 + ν3. The symmetry of this doubly excited band is the direct product of constituent modes:
\[\Gamma_{v_{1}} \otimes \Gamma_{v_{2}}=A_{1}^{\prime} \otimes E^{\prime}=E^{\prime}. \nonumber \]
and the transition \(ν_1 + ν_3\) is allowed and x, y-polarized. This \(ν_2\) vibration is IR active since \(q_2\) transforms as \(A_2”\) as does the \(\hat{z}\) operator so the \(ν_2\) vibration is z-polarized.
Overtones
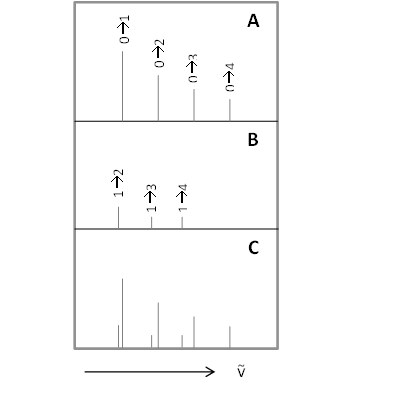
The Harmonic Oscillator approximation predicts that there will be only one line the spectrum of a diatomic molecule, and while experimental data shows there is in fact one dominant line-the fundamental--there are also other, weaker lines. How can we account for these extra lines?
These transitions are called overtones. For a simple three vibration system, An overtone transition would look like this:
\[ \psi ^{_{1}} \left( 0 \right )\psi ^{_{2}}\left ( 0 \right )\psi ^{_{3}}\left ( 0 \right )\rightarrow \psi ^{_{2}}\left ( 0 \right )\psi ^{_{2}}\left ( 2 \right )\psi ^{_{3}}\left ( 0\right ) \nonumber \]
In the IR spectrum, overtone bands are multiples of the fundamental absorption frequency. As you can recall, the energy levels in the Harmonic Oscillator approximation are evenly spaced apart. Energy is proportional to the frequency absorbed, which in turn is proportional to the wavenumber, the first overtone that appears in the spectrum will be twice the wavenumber of the fundamental. That is, first overtone \(v = 1 \rightarrow 2\) is (approximately) twice the energy of the fundamental, \(v = 0 \rightarrow 1\). This is demonstrated with the vibrations of the diatomic \(\ce{HCl}\) in the gas phase.
| Transition | Term | ṽobs [cm-1] | ṽHarmonic [cm-1] | ṽAnharmonic [cm-1] |
|---|---|---|---|---|
| \( 0 \rightarrow 1 \) | fundamental | 2,885.9 | 2,885.9 | 2,885.3 |
| \( 0 \rightarrow 2 \) | first overtone | 5,668.0 | 5,771.8 | 5,665.0 |
| \( 0 \rightarrow 3 \) | second overtone | 8,347.0 | 8,657.7 | 8,339.0 |
| \( 0 \rightarrow 4\) | third overtone | 10,923.1 | 11,543.6 | 10,907.4 |
| \( 0 \rightarrow 5\) | fourth overtone | 13,396.5 | 14,429.5 | 13,370 |
We can see from Table 1, that the anharmonic frequencies correspond much better with the observed frequencies, especially as the vibrational levels increase.
BF3 is of symmetry D3h (see https://people.chem.ucsb.edu/laverma...e/BF3_vib.html).
- The symmetric stretch, \(ν_1\), is of symmetry A1’ and is IR inactive (\(x\), \(y\) transform a \(E’\), while \(z\) transforms as \(A_2”\)).
- The \(ν_2\) vibration of symmetry \(A_2”\) and double degenerate \(E’\) vibrations \(ν_3\) (\(ν_4\)).
The first overtone of ν2 (2ν2 ) is a state with symmetry
\[A_{2}^{\prime \prime} \otimes A_{2}^{\prime \prime}=A_{1}^{\prime} \nonumber \]
and is not allowed in the IR, but the next overtone
\[A_{2}^{\prime \prime} \otimes A_{2}^{\prime \prime} \otimes A_{2}^{\prime \prime}=A_{2}^{\prime \prime} \nonumber \]
is symmetry allowed with z-polarization. The A1’ fundamentals are allowed in Raman as is the first overtone of ν2 .
Fermi Resonance
Fermi resonance is the shifting of the energies and intensities of absorption bands in an infrared or Raman spectrum. It is a consequence of quantum mechanical wavefunction mixing.
Two conditions must be satisfied for the occurrence of Fermi Resonance:
- The two vibrational modes of a molecule transform according to the same irreducible representation in their molecular point group. In other words, the two vibrations must have the same symmetries (Mulliken symbols).
- The transitions coincidentally have very similar energies.
Sometime a vibrationally excited state can have a nearby same frequency; e.g. ν1 + 2ν2 in CO2. Since ν1 = 1340 cm-1 and ν2= 2(667) = 1334 cm-1 these states can interact – provided a component of has the same symmetry as ν1. This phenomenon is call a Fermi Resonance. The interaction, as expected, looks something like the splitting we observed in a MO’s for the 1s atomic orbital in H2.

These state are mixture of \(|1,0\rangle\) and \(|0,2\rangle\) with \(\left|v_{1}, v_{2}\right\rangle\) the as the wavefunction for the molecule (vib.). So mixing gives:
\[|u p\rangle=a|10\rangle+b|02\rangle \nonumber \]
\[|l o w\rangle=b^{\prime}|10\rangle+a^{\prime}|02\rangle \nonumber \]
The for the linear \(\ce{CO2}\) molecules, the symmetry so these states are
\[\Gamma_{10}=\Sigma_{g}^{+} \nonumber \]
and
\[\Gamma_{02}=\Pi_{u} \otimes \Pi_{u} \nonumber \]
which in the D3h point group is
\[\Sigma_{g}^{+}+\Sigma_{g}^{-}+\Delta_{g} \nonumber \]
this contains the totally symmetry \(\Sigma_{g}^{+}\) representation.
So
\[\Gamma_{02}=\Pi_{u} \otimes \Pi_{u} \nonumber \]
contains the same symmetry as
\[\Gamma_{10}=\Sigma_{g}^{+} \nonumber \]
thus a Fermi resonance is allowed (still the similarity in energies is naturally required).
The \(v_1\) fundamental is allowed by Raman, as is \(2v_2\) and, but the latter is expected to be weak being an overtone. However, both \(|u p\rangle\) and \(\mid \text { low }\rangle\) bands of the Fermi Resonance doublet are intense since they both contain a large amount of \(|1,0\rangle\).

