2.8: Symmetry and Formaldehyde
- Page ID
- 364249
These five symmetry elements are tabulated in Table 2.8.1 with their corresponding operators.
| Symbol Elements | Description | Symbol Operator | Symbol |
|---|---|---|---|
| \(E\) | identity | \(\hat{E}\) | no change |
| \(C_n\) | \(n\)-fold axis of rotation | \(\hat{C}_n\) | Rotation by \(360°/n\) leaves the molecule unchanged |
| \(\sigma\) | plane of symmetry | \(\hat{\sigma}\) | Reflection in the plane leaves the molecule unchanged |
| \(i\) | center of symmetry. | \(\hat{i}\) | Inversion through the center of symmetry leaves the molecule unchanged. |
| \(S_n\) | \(n\)-fold improper rotation | \(\hat{S}_n\) | The rotary reflection operation consists of rotating through an angle \(360°/n\) about the axis, followed by reflecting in a plane perpendicular to the axis. |
Every molecule has a point group associated with it, which are assigned by a set for rules (explained by Group theory). The character tables takes the point group and represents all of the symmetry that the molecule has.
A symmetry operation is a permutation of atoms such that the molecule is transformed into a state indistinguishable from the starting state.
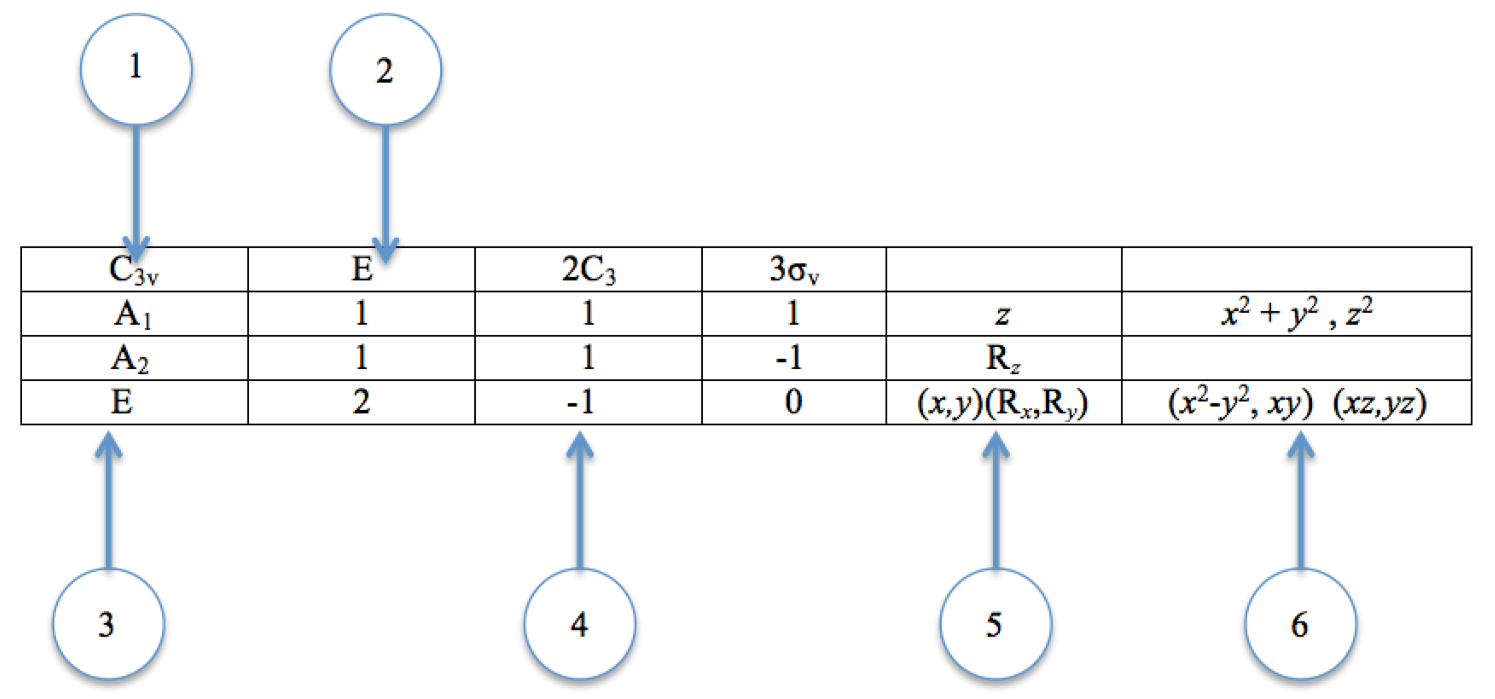
Character Tables
A character table is a two dimensional chart associated with a point group that contains the irreducible representations of each point group along with their corresponding matrix characters. It also contains the Mulliken symbols used to describe the dimensions of the irreducible representations, and the functions for symmetry symbols for the Cartesian coordinates as well as rotations about the Cartesian coordinates.
A character table can be separated into 6 different parts, namely:
- The Point Group
- The Symmetry Operation
- The Mulliken Symbols
- The Characters for the Irreducible Representations
- The Functions for Symmetry Symbols for Cartesian Coordinates and Rotations
- The Function for Symmetry Symbols for Square and Binary Products
In many applications of group theory, we only need to know the characters of the representative matrices. Luckily, when each basis function transforms as a 1D irreducible representation (which is true in many cases of interest) there is a simple shortcut to determining the characters. All we have to do is to look at the way the individual basis functions transform under each symmetry operation.
For a given operation, step through the basis functions as follows:
- Add \(1\) to the character if the basis function is unchanged by the symmetry operation (i.e. the basis function is mapped onto itself);
- Add \(-1\) to the character if the basis function changes sign under the symmetry operation (i.e the basis function is mapped onto minus itself);
- Add \(0\) to the character if the basis function moves when the symmetry operation is applied (i.e the basis function is mapped onto something different from itself).
Formaldehyde
The MO’s form a basis for irreducible representation of the \(C_{2v}\) point-group of \(\ce{H2CO}\). Conventionally, the z-axis is along the \(\ce{C=O}\) bond and the x-axis is \(┴\) to place of the molecule. The symmetry operations for \(C_{2v}\) are \(E\), \(C_2\), \(σ_v(xy)\) and \(σ_{v’}(yx)\). For :
\(π\) and \(π^{*}\)
\[\hat{E} \pi=(+1) \pi\nonumber \]
\[\hat{C}_2 \pi=(-1) \pi\nonumber \]
\[\hat{\sigma}_{v} \pi=(+1) \pi\nonumber \]
\[\hat{\sigma}_{v'} \pi=(-1) \pi\nonumber \]
So \(π\) and \(π^{*}\) transform as the \(B_1\) irreducible representation
\(σ\) and \(σ^{*}\)
\[\hat{E} \sigma=(+1) \sigma\nonumber \]
\[\hat{C}_2 \sigma=(+1) \sigma\nonumber \]
\[\hat{\sigma}_{v} \sigma=(+1) \sigma\nonumber \]
\[\hat{\sigma}_{v'} \sigma=(+1) \sigma\nonumber \]
So \(σ\) and \(σ^{*}\) transform as the \(A_1\) irreducible representation
na
\(n_a\) also transform as \(B_1\) it is a core electron in this orbital
nb
\[\hat{E} n_b=(+1) n_b\nonumber \]
\[\hat{C}_2 n_b=(-1) n_b\nonumber \]
\[\hat{\sigma}_{v} n_b=(-1) n_b\nonumber \]
\[\hat{\sigma}_{v'} n_b=(+1) n_b\nonumber \]
So \(n_b\) transforms as the \(B_2\) irreducible representation
Having ascertained the symmetry species of the MO’s: \(A_1(σ, σ^{*}, n_a)\); \(B_1(π, π^*)\); \(B_2(n)b)\), we can ask about the symmetry of the state produced by a configuration.
Direct Products of Representations
Here are listed some helpful general rules for the product of two irreducible representations. For specific combinations not listed here, one can work out the product by multiplying the characters of each irreducible representation and solving the linear combination of the irreducible representations from the point group that generates that product. Often this process is simple, especially when one or both of the irreducible representations are non-degenerate (in most cases A or B).
Representation of an Electronic State
The representation of a specific quantum electronic state can be evaluated by the direct product of the representations of the molecular orbitals of the occupied electrons. Direct products can be extracted from the tables above. For example, the non-degenerate representations below
\[A \times A = A \nonumber \]
\[B \times B = A \nonumber \]
\[A \times B = B \nonumber \]
Remember that the ground state valence electronic configuration of formaldehyde is:
\[n_{a}^{2} \sigma^{2} \pi^{2} n_{b}^{2}\left(\pi^{*}\right)^{0}\left(\sigma^{*}\right)^0 \nonumber \]
so the representation of the ground-state is
\[\Gamma = (B_1 \times B_1) (A_1 \times A_1) (B_1 \times B_1) (B_2 \times B_2) \label{pre} \]
This can be simplified using the direct product tables
\[\Gamma = (A_1) (A_1) (A_1) (A_1) \nonumber \]
so the ground state has a representation of \(A_1\). We can make a general "rule" from this. This is a “closed shell” configuration and corresponds to a state with all molecular orbitals doubly occupied or empty and must be a singlet state! Since there are no odd electrons in the orbitals in the ground state, the configuration has a \(^1A_1\) symmetry (totally symmetry).
The symmetry representation of an electronic state is the direct product of the symmetry representations of each of the odd electrons orbitals. Since doubly filled orbitals do not contribute since their products are always totally symmetry:
\[B_1 \times B_1=A_1\nonumber \]
\[A_2 \times A_{2}=A_1\nonumber \]
etc.
There are no odd electrons in the orbitals in the ground state. Possible excited state symmetry includes:
\[n_{b} \rightarrow \pi^{*} \text { or }^{1}\left(n_{b}, \pi^{*}\right)\nonumber \]
and pay attention to only the unpair electrons give the following representation
- We use lower case representations for designating 1e- orbitals.
- We use capital case representation for designated are electronic states
\[\Gamma=b_{2} \times b_{1}=A_{2}\nonumber \]
The electronic state symmetry is thus \(^1A_2\). Conventionally, the \(n_{b} \rightarrow \pi^{*}\) transition, in terms of states, is described as
\[{ }^{1} A_{2} \leftarrow{ }^{1} A_{1}\nonumber \]
or
\[{ }^{1} A_{2}\left(n, \pi^{*}\right) \leftarrow{ }^{1} A_{1}\nonumber \]
Higher energy state is conventionally places on the left hand side and the arrow points in the direction of the transition.
The \({ }^{1}\left(\pi, \pi^{*}\right)\) state has the symmetry of
\[\mathrm{b}_{1} \times \mathrm{b}_{1}=\mathrm{a}_{1}\nonumber \]
thus this transition is designated
\[{ }^{1} A_{1}\left(\pi, \pi^{*}\right) \leftarrow{ }^{1} A_{1}\nonumber \]
and this transition moves electron density from the O to the C, this is because
\[\pi=a\left(2 p_{x}^{C}\right)+b\left(2 p_{x}^{o}\right)\nonumber \]
\(b > a\) since \(O\) is more electronegative
\[\pi^{*}=b^{\prime}\left(2 p_{x}^{C}\right)+a^{\prime}\left(p_{x}^{O}\right)\nonumber \]
\(b’ > a’\) since for orthogonality with \(π\).
Now, the \({ }^{1} A_{2} \leftarrow{ }^{1} A_{1}\) transition also moves electron density from the O to the C. (For a similar argument).