2.2: Vibronic Transitions
- Page ID
- 362598
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)As mentioned Earlier, electronic excitations occur with wavelengths in the visible and ultraviolet regions of the EM spectrum. Transitions also usually involve vibrational excitations (as previously discussed with the diatomic molecule). Plot the total energy of molecule (except for nuclear translational kinetic energy) vs. \(r\), the intermolecular distance. This is effectively, the potential energy function, \(V(r)\), for the intramolecular nuclear motion (vibration). This is due to the Born-Oppenheimer approximation. Often, we introduce vibrations as a quadratic function (Harmonic Oscillator), however, a Morse potential function gives a good fit to the true potential (within the BO approximation).
\[V(r)=D\left(1-\mathrm{e}^{-v_{o}\left(2 \pi^{2} / D\right)^{1 / 2}\left(r-r_{e q}\right)}\right)^{2} \nonumber \]
where \(D\) is the dissociation energy, \(μ\) is the reduced mass, \(r_{eq}\) is the equilibrium bond length and \(\nu_o\) is the fundamental vibrational frequency.
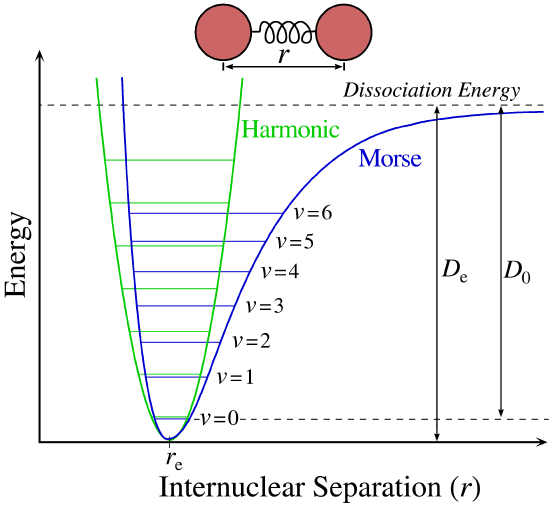
The actual energy levels for the molecule are shown by the horizontal lines. These lie above \(V(r)\) and represent the contributions of nuclear kinetics energy of the total energy of the molecule. The classical turning points for a given vibrational state (\(v=3\)) are shown by point A and B. At these points, classically, the nuclear kinetic energy is 0 and the vibrational energy is all potential. At \(r=r_{eq}\), the kinetic Energy of the nuclear, classically, is at the maximum, which is where \(V(r)\) is 0.
In quantum mechanics, it does not quite work that way. The only things we know is that \(\langle V \rangle_{av}=\langle T\rangle\) on the average. Note that the spacing between the vibration energy levels decrease with increasing vibrational energy. If enough energy is absorbed, the molecule will dissociate into atoms. The vibration spacing becomes smaller since the bond is not an ideal Hook’s law spring: \(V(r)=1/2k(r-r_{eq})\), and becomes weaker as it is stretched, thus \(Δν\) decreases between adjacent energy levels.
Each bound state also can be described by a different (in general) Morse potential curve, displaced upwards by the electronic energy different. \(V_o\), \(r_{eq}\), and \(D\) will differ in principle for each vibration (if more than two atoms in the molecule) in each electronic state (Figure \(\PageIndex{3}\)).
Transitions usually originate from the v=0 (because they are not thermally occupied at kT=200 cm-1), but can end up in \(v’=0\), \(v’=1\), \(v’’=2\) etc. No selection rules on this transition. Electronic transitions in molecules are governed by the Frank-Condon approximation. Since an electronic transition task place in a short time (1fs), the nuclei do not have time to move during an electronic transition (similar separation of velocities as in the Born Oppenheimer approximation, but that did not involve spectroscopic transitions). Thus, all transitions are vertical on a potential energy diagram (plotted energy versus nuclear position) = \(r\) is fixed in a diatomic. Note: the vibrational wavefunctions are drawn above.
The Born-Oppenheimer approximation allows us to write the wavefunction of a state as
\[\Psi_{\text {int }}=\Psi_{e l} \Psi_{\text {nucl }}(Q) \nonumber \]
where Q is the nuclear distances or positions. To be more exact, we should
\[\psi_{\text {int }}=\Psi_{e l}(q ; Q) \psi_{\text {nucl }}(Q) \nonumber \]
with \(q\) representing the electron distances (or positions). The semi-colon represents a parametric dependence on \(Q\).
The separation of the internal wavefunction (excluding transitional effects) into a product of two functions is the same as splitting the Hamiltonian into a sum of two components
\[H_{\mathrm{int}}=\Psi_{e l}(q ; Q)+\Psi_{m c l}(q) \nonumber \]
and the corresponding energies
\[E_{\text {int }}=E_{e l}+E_{\text {nucl }} . \nonumber \]
If \(\ce{H^{(1)}}\) is the interaction of the electromagnetic radiation with the electrons, then the integral
\[\int \psi_{\text {int }}^{i} H^{(1)} \psi_{\text {int }}^{f} d \Gamma \nonumber \]
can be factored and do NOT depend on vibration (just parametrically). So
\[\int \psi_{\text {int }}^{i} H^{(1)} \psi_{\text {int }}^{f} d \Gamma=\int \psi_{e l}^{i} H^{(1)} \psi_{e l}^{f} d \Gamma \times \int \psi_{\text {mucl }}^{i} \psi_{\text {mucl }}^{f} d Q \nonumber \]
And the transition probability is
\[W_{i \rightarrow f} \propto\left|\int \psi_{e l}^{i} H^{(1)} \psi_{e l}^{f} d\right|^{2} \times\left|\int \psi_{\text {nucl }}^{i} \psi_{\text {nucl }}^{f} d Q\right|^{2} \nonumber \]
The last term is the square of the nuclear overlap integral and is call the Frank-Condon (FC) Factor. This first term is an integral over the electronic wavefunction as this does not depend strongly on the nuclear coordinate (well, parametrically). So the intensity of the v=0 to v’=0, v=0 to v’=1, and v=0 to v’=2, transitions is mainly controlled by the Franck-Condon factor also referred to as \(S\).
To see which vibrational mode changes can accompany an electronic transition, we need to look at the Franck-Condon (FC) factors
Franck-Condon Progressions
To understand the significance of the above formula for the FC factor, let us examine a ground and excited state potential energy surface at \(T = 0\) Kelvin. Shown below are two states separated by 8,000 cm-1 in energy. This is energy separation between the bottoms of their potential wells, but also between the respective zero-point energy levels. Let us assume that the wavenumber of the vibrational mode is 1,000 cm-1 and that the bond length is increased due to the fact that an electron is removed from a bonding orbital and placed in an anti-bonding orbital upon electronic excitation.
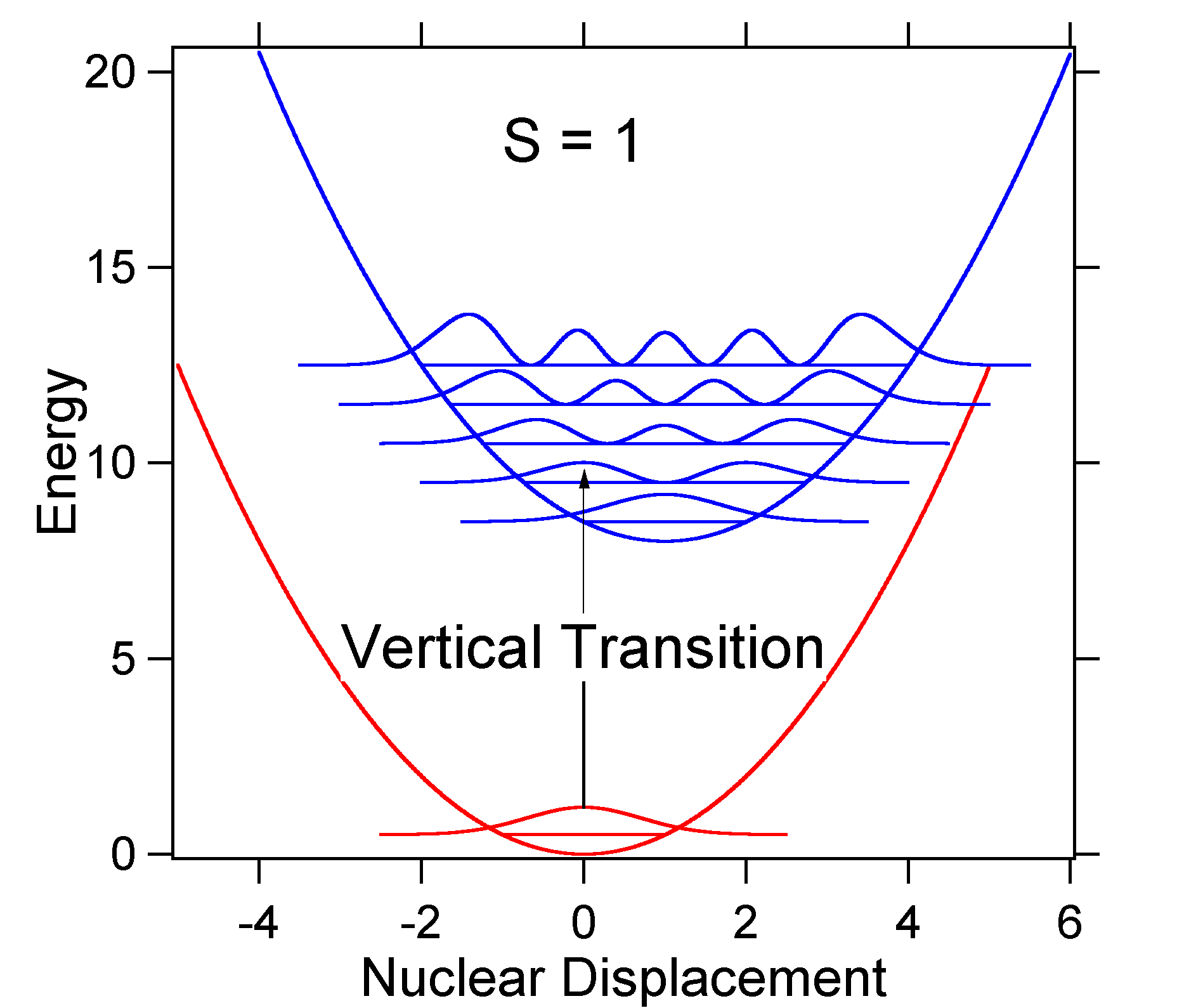
According to the above model for the Franck-Condon factor we would generate a "stick" spectrum (Figure \(\PageIndex{3}\)) where each vibrational transition is infinitely narrow and transition can only occur when \(E = h\nu\) exactly. For example, the potential energy surfaces were given for \(S = 1\) and the transition probability at each level is given by the sticks (black) in Figure \(\PageIndex{3}\).
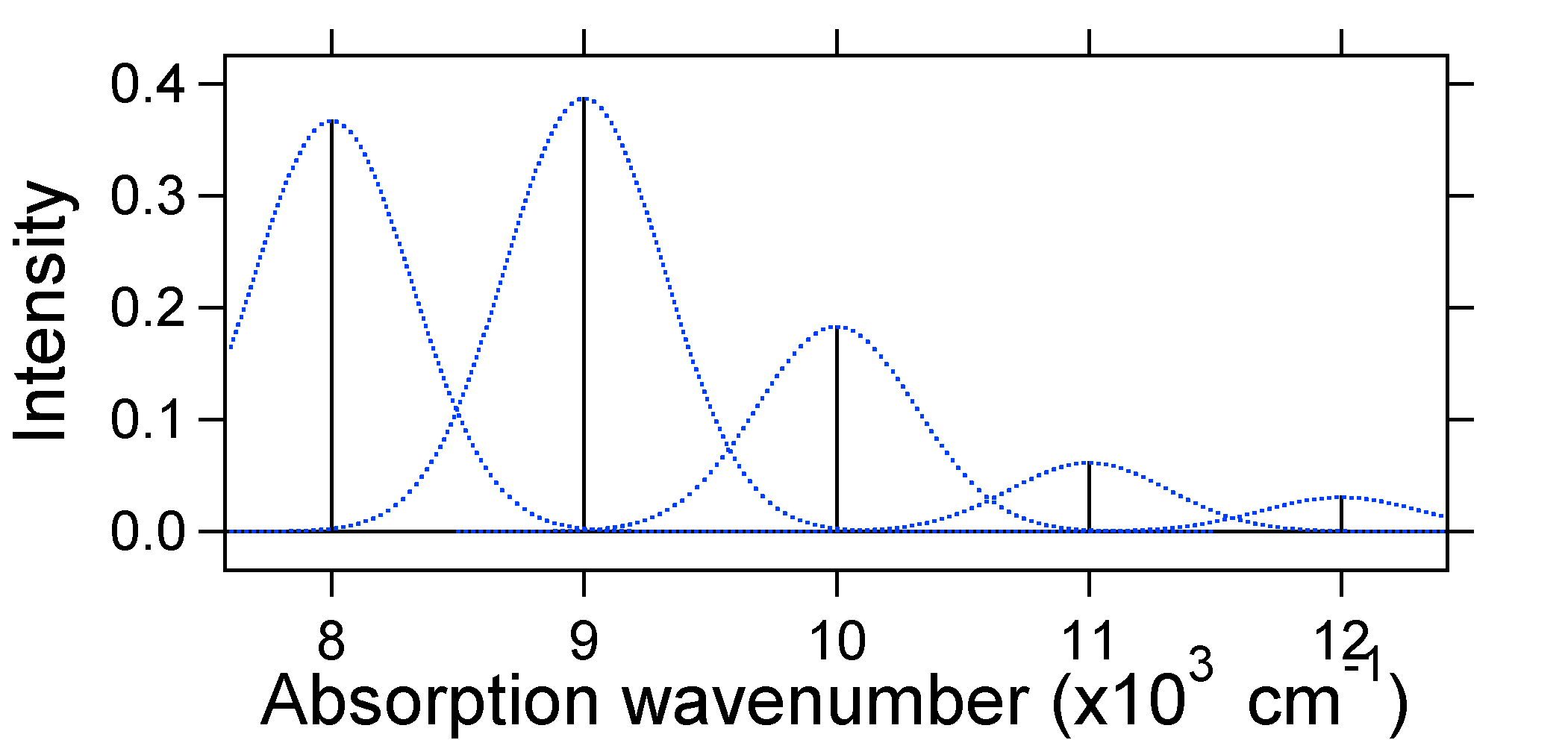
The dotted Gaussians that surround each stick give a more realistic picture of what the absorption spectrum should look like. In this first place each energy level (stick) will be given some width by the fact that the state has a finite lifetime. Such broadening is called homogeneous broadening since it affects all of the molecules in the ensemble in a similar fashion. There is also broadening due to small differences in the environment of each molecule. This type of broadening is called inhomogeneous broadening. Regardless of origin the model above was created using a Gaussian broadening
The nuclear displacement between the ground and excited state determines the shape of the absorption spectrum. Let us examine both a smaller and a large excited state displacement. If \(S = ½\) and the potential energy surfaces in this case are:
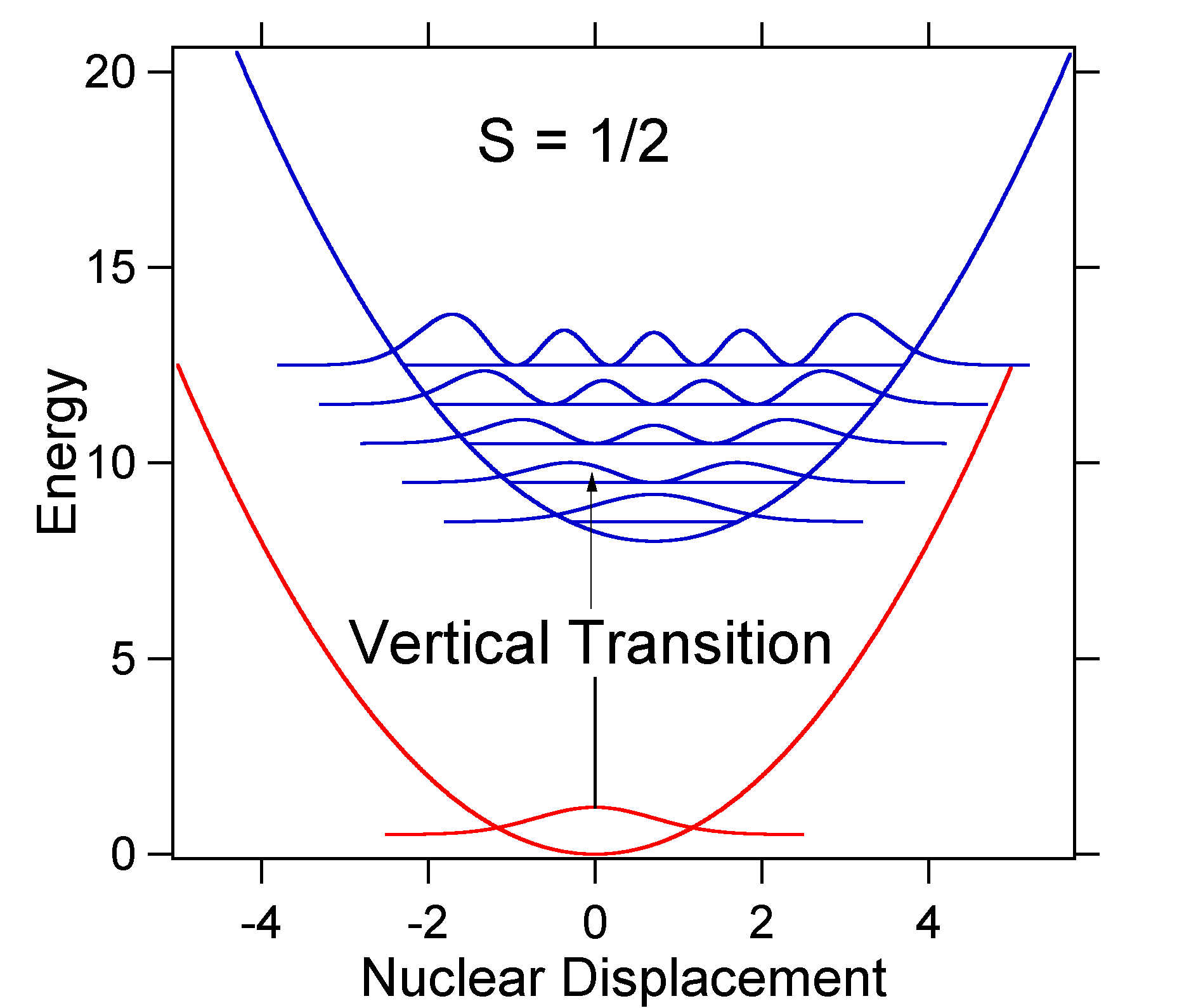
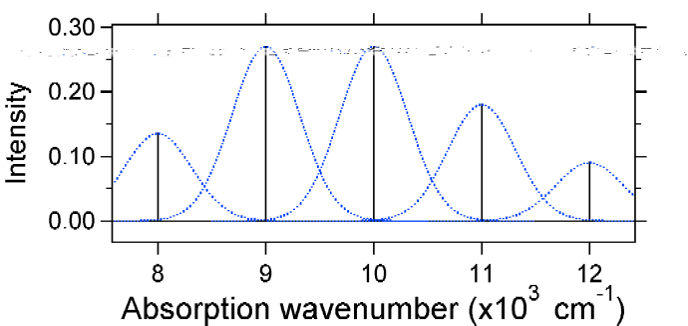
For this case the "stick" spectrum has the appearance in Figure \(\PageIndex{5}\)
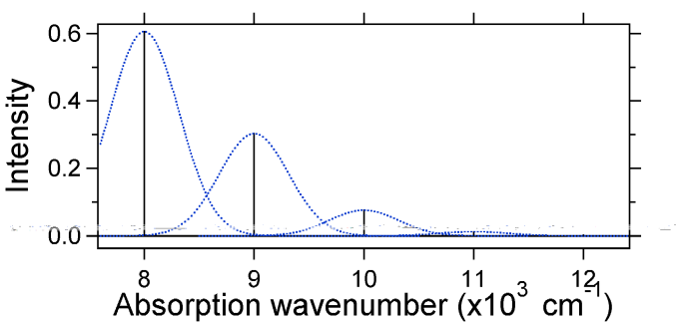
Note that the zero-zero or \(S_{0,0}\) vibrational transition is much large in the case where the displacement is small.
As a general rule of thumb the \(S\) constant gives the ratio of the intensity of the \(v = 2\) transition to the \(v = 1\) transition. In this case since \(S = 0.5\), the \(v=2\) transition is 0.5 the intensity of \(v=1\) transition.
As an example of a larger displacement the disposition of the potential energy surfaces for S = 2 is shown below.
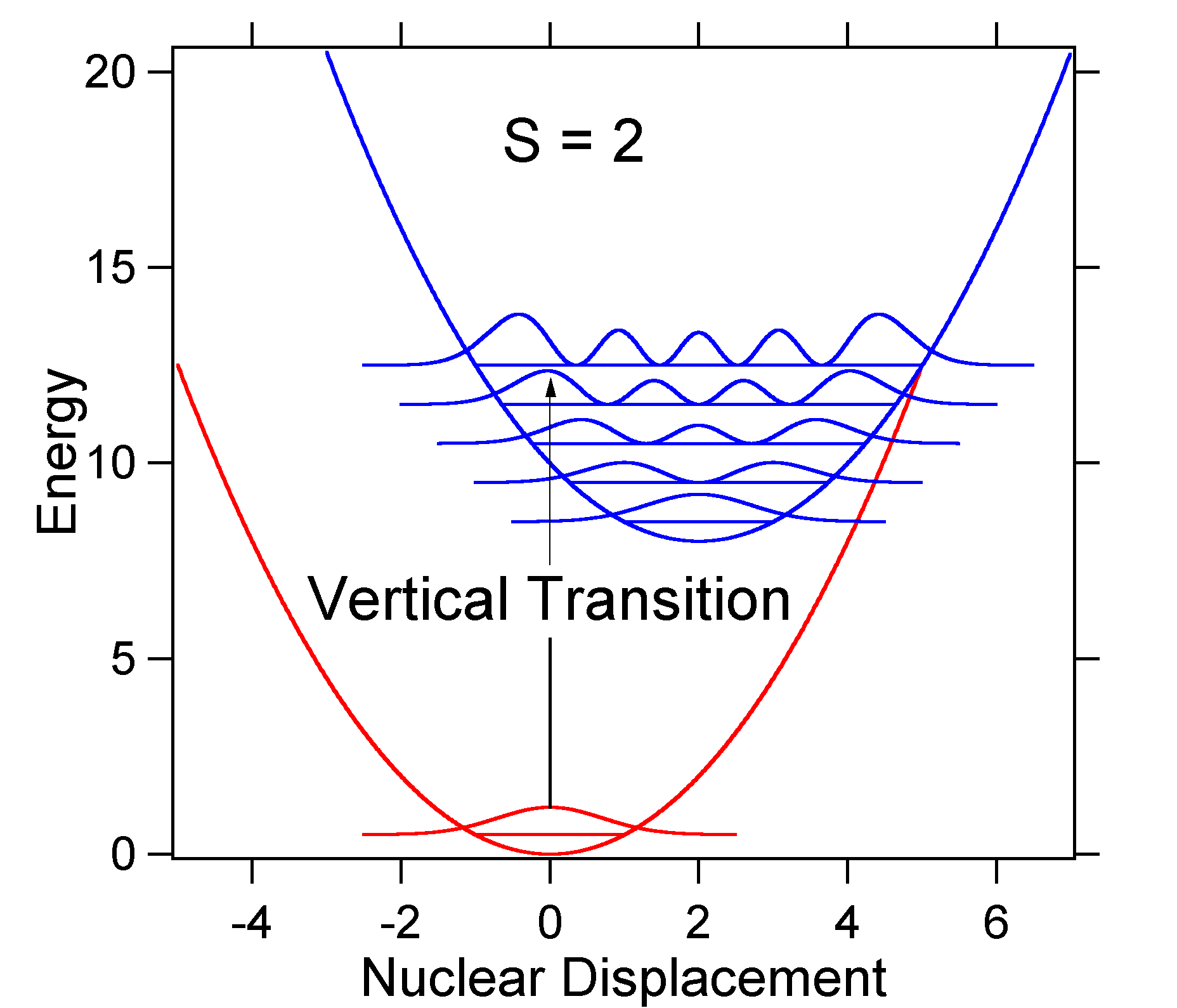
The larger displacement results in decreased overlap of the ground state level with the v = 0 level of the excited state. The maximum intensity will be achieved in higher vibrational levels as shown in the stick spectrum.
The absorption spectra plotted below all have the same integrated intensity, however their shapes are altered because of the differing extent of displacement of the excited state potential energy surface.
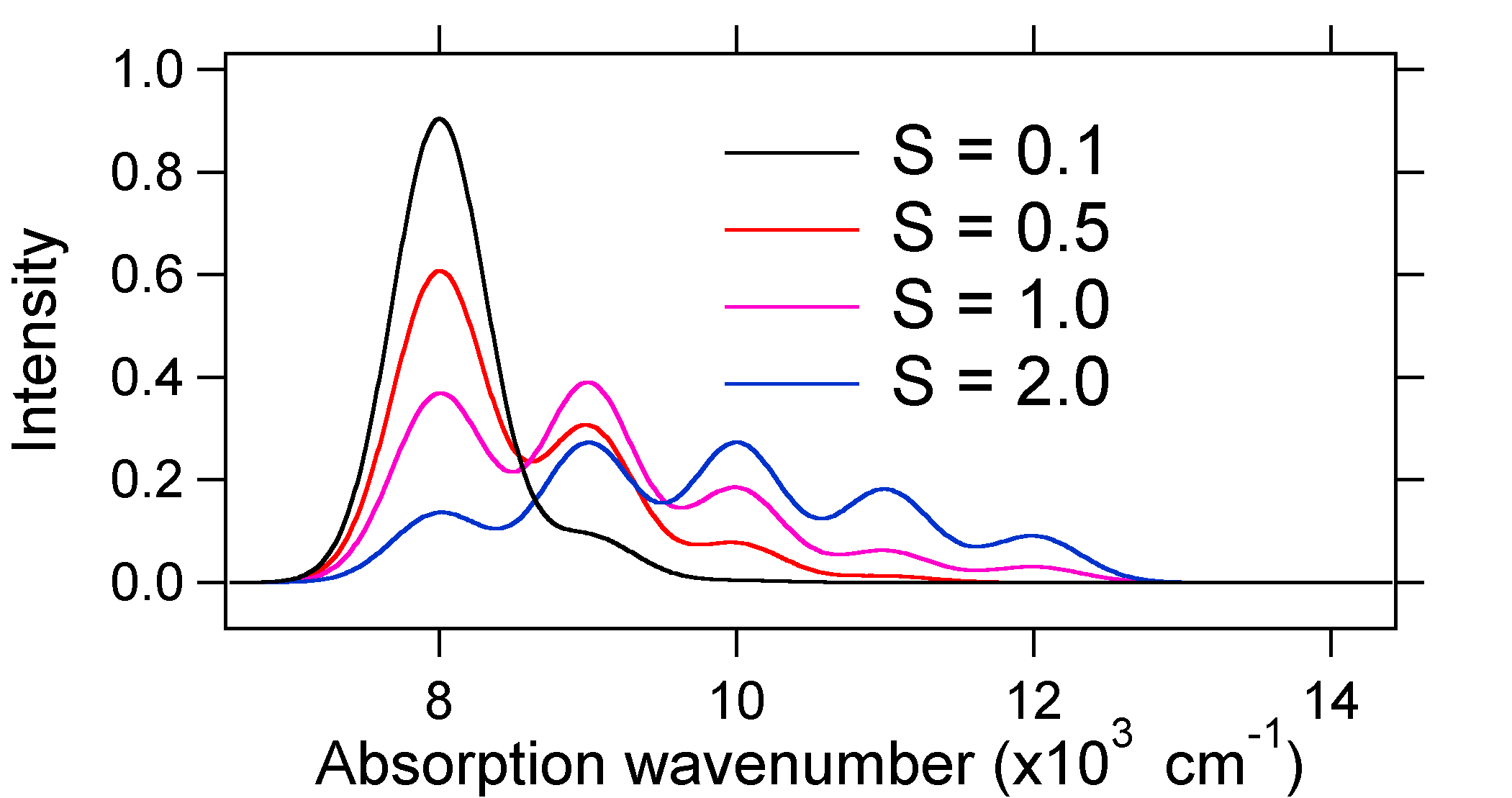
So the nature of the relative vibronic band intensities can tell us whether there is a displacement of the equilibrium nuclear coordinate that accompanied a transition. When will there be an increase in bond length (i.e., \(Q_e > R_e\))? This occurs when an electron is promoted from a bonding molecular orbital to a non-bonding or anti-bonding molecular orbitals (i.e., when the bond order is less in the excited state than the ground state).
- Non-bonding molecular orbital \(\rightarrow\) bonding molecular orbital
- Anti-bonding molecular orbital \(\rightarrow\) bonding molecular orbital
- Anti-bonding molecular orbital \(\rightarrow\) non-bonding molecular orbital
In short, when the bond order is lower in the excited state than in the ground state, then \(Q_e > R_e\); an increase in bond length will occur when this happens.

