16.2: van der Waals and Redlich-Kwong Equations
- Page ID
- 57448
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The ideal gas law is valid for low pressures, where the finite volume of particles and intermolecular attractions do not have a large impact. At higher pressures, we must account for these factors. The van der Waals and Redlich-Kwong equations of states are equations of state that attempt to account for real gas behavior by modifying the ideal gas law with two additional parameters.
The Van der Waals Equation of State
The van der Waals Equation of State is an equation relating the density of gases and liquids to the pressure, volume, and temperature conditions (i.e., it is a thermodynamic equation of state). It can be viewed as an adjustment to the ideal gas law that takes into account the non-zero volume of gas molecules and inter-particle attraction using correction terms \(a\) and \(b\). It was derived in 1873 by Johannes Diderik van der Waals, who received the Nobel Prize in 1910 for this work. The van der Waals equation of state is:
\[P = \dfrac{nRT}{V - nb} - \dfrac{an^2}{V^2} \label{Eq7} \]
Equation \(\ref{Eq7}\) can also be rewritten as
\[\left(P+{\dfrac {n^{2}a}{V^{2}}}\right)\left(V-nb\right)=nRT \nonumber \]
If the correction terms \(a\) and \(b\) go to zero, the equation reduces to the ideal gas equation of state:
\[PV=nRT \nonumber \]
Let's first look first at the correction term \(b\), which represents the volumes of the particles and assumes a hard-wall potential, \(u_o(r)\). This potential energy term describes a system of hard sphere “billiard balls” of diameter \(\sigma\). Figure 16.2.1 shows two of these billiard ball type particles at the point of contact (i.e, the distance of closest approach). At this point, they undergo a collision and separate, so they cannot be closer than that distance.

The distance between their centers is also \(\sigma\). Because of this distance of closest approach, the total volume available to the particles is not the volume of the container, \(V\), but some volume less than \(V\). This reduction in volume can be calculated. Figure 16.2.1 shows a shaded sphere that just contains the pair of billiard ball particles. The volume of this sphere is the volume excluded from any two particles. The radius of the sphere is \(\sigma\) and the excluded volume for the two particles is \(4 \pi \sigma^3/3\), which is the volume of the shaded sphere. From this, we see that the excluded volume for any one particle is just half of this or \(\frac{2}{3} \pi \sigma^3\). The excluded volume for a mole of such particles is the parameter \(b\):
\[b = \dfrac{2}{3} \pi \sigma^3 N_0 \nonumber \]
Given \(n\) moles of gas, the total excluded volume is then \(nb\), so that the total available volume is \(V - nb\).
Let's turn our attention the \(a\), which represents the intermolecular attractions of the particles. Molecular attractions tend to make the \(P\) exerted by the gas less than that predicted by the ideal gas law at low pressures. \(P\) is force over area:
\[P=\frac{F}{A} \nonumber \]
Pressure is proportion to the net force on the wall of the container:
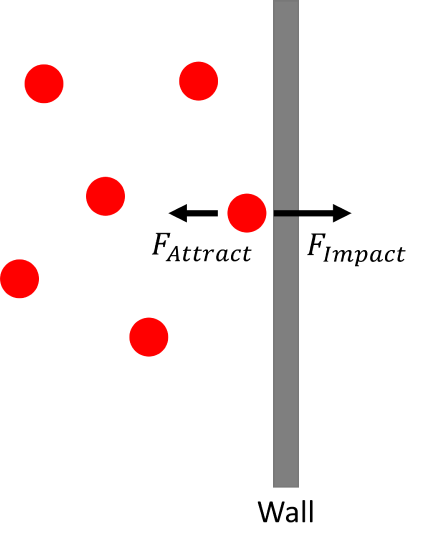
The net force is the force of the molecules impacting the container wall minus the intermolecular attraction of the molecules:
\[{\bar{F}}_{Net}={\bar{F}}_{Impact}-{\bar{F}}_{Attract} \nonumber \]
Therefore, the pressure will be less for the real gas than the ideal gas. We can add a correction term to pressure to account for intermolecular attractions:
\[P_{VDW}=P_{Real}+a\left(?\right) \nonumber \]
\(V\) does influence the amount of intermolecular attraction because \(P\) is reduced as \(V\) is increased:
\[P\propto\frac{1}{V} \nonumber \]
And pressure is proportional to the number of attractive interactions:
# of molecular interactions \(\propto P^2\)
# of molecular interactions \(\propto \frac{1}{V^2}\)
We now have an expression for the van der Waals \(P\):
\[P=P_{Real}+\frac{an^2}{V^2} \nonumber \]
The constants \(a\) and \(b\) depend on the substance. Some typical values are:1
| Molecule | \(a\;\sf\left(\frac{L^2\cdot bar}{{mol}^2}\right)\) | \(b\;\sf\left(\frac{L}{mole}\right)\) |
|---|---|---|
| \(\sf H_2O\) | 5.536 | 0.03049 |
| \(\sf N_2\) | 1.43 | 0.03913 |
| \(\sf CH_4\) | 2.283 | 0.04278 |
| \(\sf C_2H_6\) | 5.562 | 0.0638 |
1. R. C. Weast (1972). Handbook of Chemistry and Physics 53rd Edition. Chemical Rubber Pub.
Redlich-Kwong Equation of State
The van der Waals Equation of State had to wait almost 100 years before a real, successful improvement was introduced to it. This progress occurred once researchers committed themselves to finding the empirical temperature dependency of the attraction parameter \(a\) proposed by van der Waals. In contrast, very little attention has been paid to modifying the parameter \(b\) for co-volume. It makes a lot of sense that \(b\) would not be modified by temperature, because it represents the volume of the molecules, which should not be affected by their kinetic energy (measured in terms of temperature). The very first noteworthy successful modification to the attraction parameter came with the publication of the equation of state of Redlich-Kwong in 1949.
The Redlich–Kwong equation of state is an empirical, algebraic equation that relates temperature, pressure, and volume of gases. It is generally more accurate than the van der Waals and the ideal gas equations of state at temperatures above the critical temperature. It was formulated by Otto Redlich and Joseph Neng Shun Kwong in 1949, who showed that a simple two-parameter equation of state could well reflect reality in many situations. Redlich and Kwong revised the van der Waals Equation of State (Equation \(\ref{Eq7}\)) and proposed the following expressions:
\[ \left( P + \dfrac{a}{\sqrt{T} \bar{V} (\bar{V} + b)} \right) ( \bar{V}-b) = RT \label{10.1} \]
The fundamental change they introduced was to the functional form of \(\partial P_\text{attraction}\). Additionally, they introduced the co-volume \(b\) into the denominator of this functional form. The important concept here is that the attraction parameter \(a\) of van der Waals needed to be made a function of temperature to do a better job of quantitatively matching experimental data. This was a realization that van der Waals had suggested, but no actual functional dependency had been introduced until the Redlich-Kwong equation.
We know what follows at this point. To come up with an expression for \(a\) and \(b\) of Equation \(\ref{10.1}\), we apply the criticality conditions to this equation of state. As we recall, imposing the criticality conditions allows us to relate the coefficients \(a\) and \(b\) to the critical properties (\(P_c\), \(T_c\)) of the substance. Once we have done that, we obtain the definition of \(a\) and \(b\) for the Redlich-Kwong equation of state:
\[ a =0.42780 \dfrac{R^2T_c^{2.5}}{P_c} \label{10.2a} \]
\[ b =0.086640 \dfrac{RT_c}{P_c} \label{10.2b} \]
The Redlich-Kwong equation of state radically improved, in a quantitative sense, the predictions of the van der Waals equation of state. We now recall that van der Waals-type equations are cubic because they are cubic polynomials in molar volume and compressibility factor. It comes as no surprise then, that we can transform Equation \(\ref{10.1}\) into:
\[ \bar{v} ^3 - \left( \dfrac{RT}{P} \right)\bar{v}^2 + \dfrac{1}{P} \left( \dfrac{1}{T^{0.5}} - bRT - Pb^2 \right) \bar{v} - \dfrac{ab}{PT^{0.5}} = 0 \label{10.3} \]
and, by defining the following parameters:
\[ A = \dfrac{aP}{R^2T^{2.5}} \label{10.3a} \]
\[ B =\dfrac{bP}{RT} \label{10.3b} \]
and introducing the compressibility factor definition:
\[Z = \dfrac{P\bar{v}}{RT} \nonumber \]
we get:
\[ Z^3 -Z^2 + (A -B -B^2) Z -AB =0 \label{10.4} \]
We may also verify the two-parameter corresponding state theory by introducing Equations \(\ref{10.2a}\), \(\ref{10.2b}\), and \(\ref{10.3}\) into Equation \(\ref{10.4}\):
\[Z^3−Z^2+\dfrac{P_r}{T_r} \left( \dfrac{0.42748}{T_r^{1.5}} −0.08664−0.007506 \dfrac{P_r}{T_r} \right)Z−0.03704 \dfrac{P^2_r}{T^{3.5}_r}=0 \label{10.5} \]
Where:
\[P_r=\frac{P}{P_c} \nonumber \]
\[T_r=\frac{T}{T_c} \nonumber \]
\(P_r\) and \(T_r\) are the pressure and temperature at the reduced state. See Section 16.4 for more information on reduced states. In Equation \(\ref{10.5}\), we can observe the same thing that we saw with the van der Waals equation of state: gases at corresponding states have the same properties. Equation \(\ref{10.5}\) is particularly clear about it: any two different gases at the same \(P_r\), \(T_r\) condition have the same compressibility factor.
Just as any other cubic equation of state, Equations \(\ref{10.1}\) through \(\ref{10.5}\), as they stand, are to be applied to pure substances. For mixtures, however, we apply the same equation, but we impose certain mixing rules to obtain \(a\) and \(b\), which are functions of the properties of the pure components. Strictly speaking, we create a new “pseudo” pure substance that has the average properties of the mixture. Redlich-Kwong preserved the same mixing rules that van der Waals proposed for his eqution of state:
\[ a_m = \sum_i \sum_j y_iy_j a_{ij} \nonumber \]
with
\[a_{ij} = \sqrt{a_ia_j} \nonumber \]
and
\[ b_{m}=\sum_i y_ib_i \nonumber \]
Naturally, Redlich and Kwong did not have the last word on possible improvements to the van der Waals equation of state. The Redlich-Kwong equation of state, as shown here, is no longer used in practical applications. Research continued and brought with it new attempts to improve the Redlich-Kwong equation of state. After more than two decades, a modified Redlich-Kwong equation of state with very good potential was developed.
Contributors and Attributions
Michael Adewumi (The Pennsylvania State University) Vice Provost for Global Program, Professor of Petroleum and Natural Gas Engineering
Jerry LaRue (Chapman University)

