2.5: The Effect of Temperature on Reaction Rates
- Page ID
- 20274
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
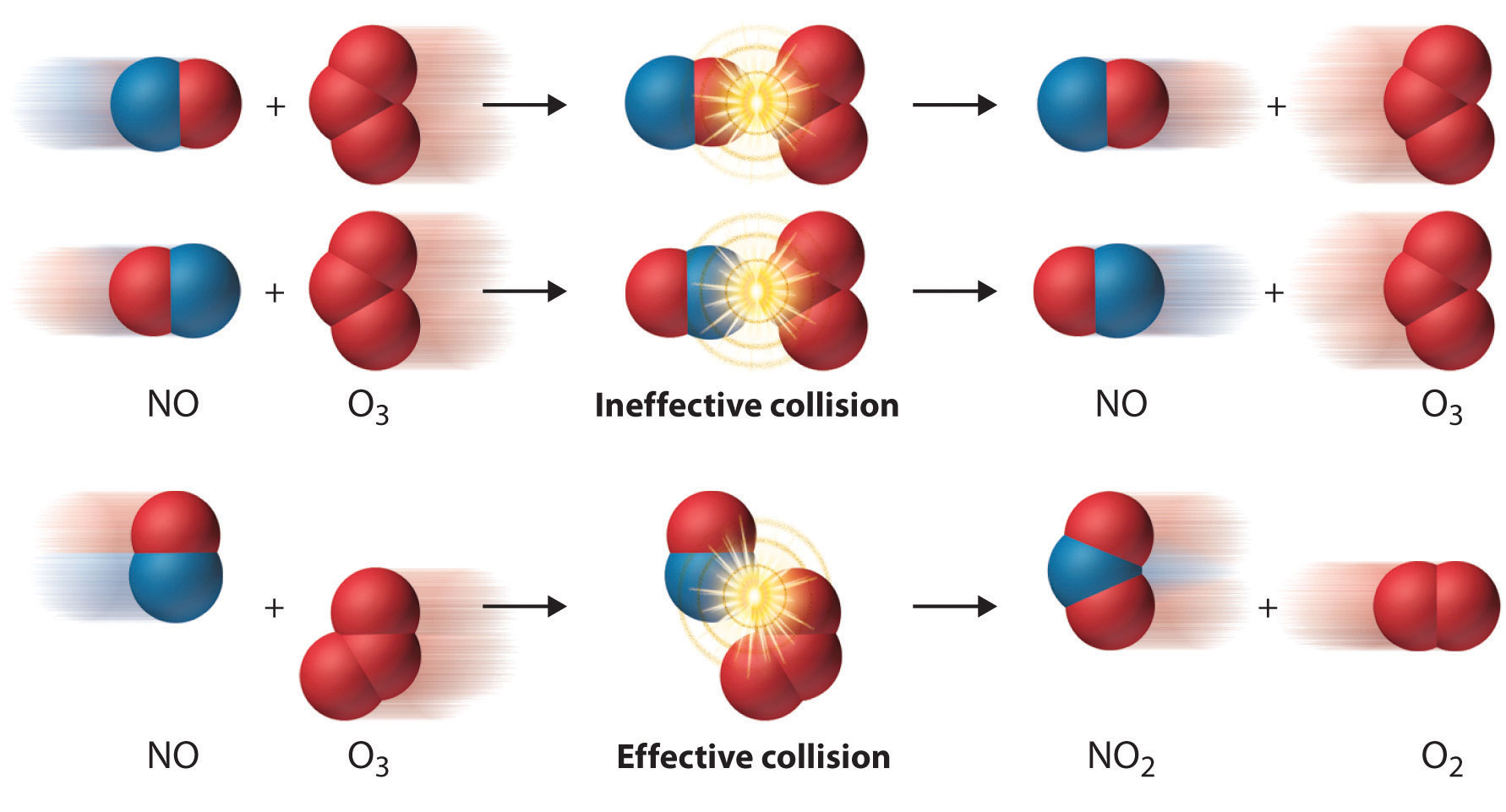
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)When molecules collide, the kinetic energy of the molecules can be used to stretch, bend, and ultimately break bonds, leading to chemical reactions. If molecules move too slowly with little kinetic energy, or collide with improper orientation, they do not react and simply bounce off each other. However, if the molecules are moving fast enough with a proper collision orientation, such that the kinetic energy upon collision is greater than the minimum energy barrier, then a reaction occurs. The minimum energy requirement that must be met for a chemical reaction to occur is called the activation energy, \(E_a\).

The reaction pathway is similar to what happens in Figure \(\PageIndex{1}\). To get to the other end of the road, an object must roll with enough speed to completely roll over the hill of a certain height. The faster the object moves, the more kinetic energy it has. If the object moves too slowly, it does not have enough kinetic energy necessary to overcome the barrier; as a result, it eventually rolls back down. In the same way, there is a minimum amount of energy needed in order for molecules to break existing bonds during a chemical reaction. If the kinetic energy of the molecules upon collision is greater than this minimum energy, then bond breaking and forming occur, forming a new product (provided that the molecules collide with the proper orientation).
The activation energy (\(E_a\)), labeled \(\Delta{G^{\ddagger}}\) in Figure \(\PageIndex{2}\), is the energy difference between the reactants and the activated complex, also known as transition state. In a chemical reaction, the transition state is defined as the highest-energy state of the system. If the molecules in the reactants collide with enough kinetic energy and this energy is higher than the transition state energy, then the reaction occurs and products form. In other words, the higher the activation energy, the harder it is for a reaction to occur and vice versa.
Overcoming the energy barrier from thermal energy involves addressing the fraction of the molecules that possess enough kinetic energy to react at a given temperature. According to kinetic molecular theory, a population of molecules at a given temperature is distributed over a variety of kinetic energies that is described by the Maxwell-Boltzman distribution law.
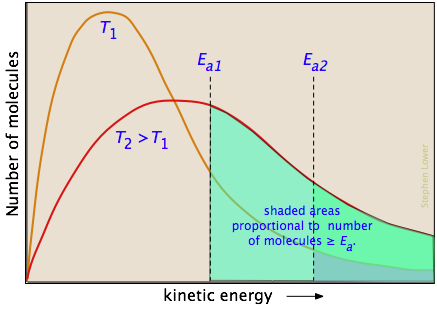
The two distribution plots shown here are for a lower temperature T1 and a higher temperature T2. The area under each curve represents the total number of molecules whose energies fall within particular range. The shaded regions indicate the number of molecules which are sufficiently energetic to meet the requirements dictated by the two values of Ea that are shown. It is clear from these plots that the fraction of molecules whose kinetic energy exceeds the activation energy increases quite rapidly as the temperature is raised. This the reason that virtually all chemical reactions (and all elementary reactions) proceed more rapidly at higher temperatures.
Arrhenius Equation
By 1890 it was common knowledge that higher temperatures speed up reactions, often doubling the rate for a 10-degree rise, but the reasons for this were not clear. Finally, in 1899, the Swedish chemist Svante Arrhenius (1859-1927) combined the concepts of activation energy and the Boltzmann distribution law into one of the most important relationships in physical chemistry:
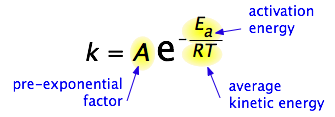
Take a moment to focus on the meaning of this equation, neglecting the A factor for the time being. First, note that this is another form of the exponential decay law discussed in the previous section of this series. What is "decaying" here is not the concentration of a reactant as a function of time, but the magnitude of the rate constant as a function of the exponent –Ea /RT. And what is the significance of this quantity? Recalling that RT is the average kinetic energy, it becomes apparent that the exponent is just the ratio of the activation energy Ea to the average kinetic energy. The larger this ratio, the smaller the rate (hence the negative sign). This means that high temperature and low activation energy favor larger rate constants, and thus speed up the reaction. Because these terms occur in an exponent, their effects on the rate are quite substantial.
Svante August Arrhenius
Svante August Arrhenius (19 February 1859 – 2 October 1927) was a Swedish scientist, originally a physicist, but often referred to as a chemist, and one of the founders of the science of physical chemistry. He received the Nobel Prize for Chemistry in 1903, becoming the first Swedish Nobel laureate, and in 1905 became director of the Nobel Institute where he remained until his death. The Arrhenius equation, Arrhenius definition of an acid, lunar crater Arrhenius, the mountain of Arrheniusfjellet and the Arrhenius Labs at Stockholm University are named after him. Today, Arrhenius is best known for his study published in 1896, on the greenhouse effect.

The two plots in Figure \(\PageIndex{4}\) show the effects of the activation energy (denoted here by E‡) on the rate constant. Even a modest activation energy of 50 kJ/mol reduces the rate by a factor of 108.
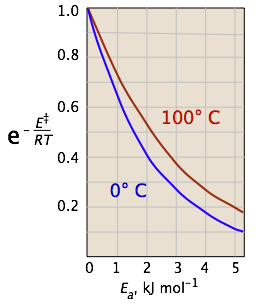
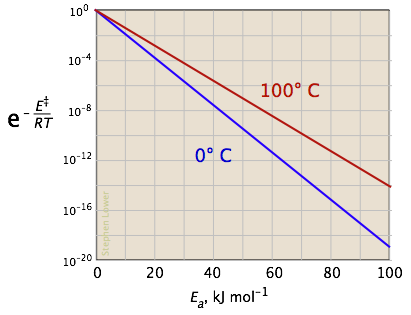
Looking at the role of temperature, a similar effect is observed. (If the x-axis were in "kilodegrees" the slopes would be more comparable in magnitude with those of the kilojoule plot at the above right.)
Determining the activation energy
The Arrhenius equation
\[k = A e^{-E_a/RT} \label{1}\]
can be written in a non-exponential form that is often more convenient to use and to interpret graphically (Figure \(\PageIndex{4}\)). Taking the logarithms of both sides and separating the exponential and pre-exponential terms yields
\[ \ln k = \ln \left(Ae^{-E_a/RT} \right) = \ln A + \ln \left(e^{-E_a/RT}\right) \label{2}\]
\[\ln k = \ln A + \dfrac{-E_a}{RT} = \left(\dfrac{-E_a}{R}\right) \left(\dfrac{1}{T}\right) + \ln A \label{3}\]
which is the equation of a straight line whose slope is \(–E_a /R\). This affords a simple way of determining the activation energy from values of k observed at different temperatures, by plotting \(\ln k\) as a function of \(1/T\).
Example \(\PageIndex{1}\): Isomerization of Cyclopropane
For the isomerization of cyclopropane to propene,

the following data were obtained (calculated values shaded in pink):
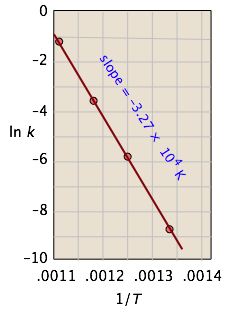
| T, °C | 477 | 523 | 577 | 623 |
|---|---|---|---|---|
| 1/T, K–1 × 103 | 1.33 | 1.25 | 1.18 | 1.11 |
| k, s–1 | 0.00018 | 0.0027 | 0.030 | 0.26 |
| ln k | –8.62 | –5.92 | –3.51 | –1.35 |
From the calculated slope, we have
– (Ea/R) = –3.27 × 104 K
Ea=– (8.314 J mol–1 K–1) (–3.27 × 104 K) = 273 kJ mol–1
This activation energy is high, which is not surprising because a carbon-carbon bond must be broken in order to open the cyclopropane ring. (C–C bond energies are typically around 350 kJ/mol.) This is why the reaction must be carried out at high temperature.
Calculating \(E_a\) without a plot
Because the ln k vs.-1/T plot yields a straight line, it is often convenient to estimate the activation energy from experiments at only two temperatures. The ln A term is eliminated by subtracting the expressions for the two ln-k terms via the following steps:
\[ \ln k_{1}=\ln A - \dfrac{E_{a}}{k_{B}T_1} \]
at \(T_1\) and
\[ \ln k_{2}=\ln A - \dfrac{E_{a}}{k_{B}T_2} \]
at \(T_2\). By rewriting the second equation:
\[ \ln A = \ln k_{2} + \dfrac{E_{a}}{k_{B}T_2} \]
and substitute for \(\ln A\) into the first equation:
\[ \ln k_{1}= \ln k_{2} + \dfrac{E_{a}}{k_{B}T_2} - \dfrac{E_{a}}{k_{B}T_1} \]
This simplifies to:
\[ \ln k_{1} - \ln k_{2} = -\dfrac{E_{a}}{k_{B}T_1} + \dfrac{E_{a}}{k_{B}T_2} \]
\[ \ln \dfrac{k_{1}}{k_{2}} = -\dfrac{E_{a}}{k_{B}} \left (\dfrac{1}{T_1}-\dfrac{1}{T_2} \right )\]
Example \(\PageIndex{2}\)
A widely used rule-of-thumb for the temperature dependence of a reaction rate is that a ten degree rise in the temperature approximately doubles the rate. This is not generally true, especially when a strong covalent bond must be broken. For a reaction that does show this behavior, what would the activation energy be?
Solution
Center the ten degree interval at 300 K. Substituting into the above expression yields
\[E_a = \dfrac{(8.314)(\ln 2/1)}{\dfrac{1}{295} – \dfrac{1}{305}} = \dfrac{(8.314)(0.693)}{0.00339 K^{-1} – 0.00328 \; K^{-1}} \]
= (5.76 J mol–1 K–1) / (0.00011 K–1) = 52400 J mol–1 = 52.4 kJ mol–1
Example \(\PageIndex{3}\)
It takes about 3.0 minutes to cook a hard-boiled egg in Los Angeles, but at the higher altitude of Denver, where water boils at 92°C, the cooking time is 4.5 minutes. Use this information to estimate the activation energy for the coagulation of egg albumin protein.
Solution
The ratio of the rate constants at the elevations of Los Angeles and Denver is 4.5/3.0 = 1.5, and the respective temperatures are \(373 \; \rm{K }\) and \(365\; \rm{K}\). With the subscripts 2 and 1 referring to Los Angeles and Denver respectively:
\[E_a = \dfrac{(8.314)(\ln 1.5)}{\dfrac{1}{365\; \rm{K}} – \dfrac{1}{373 \; \rm{K}}} = \dfrac{(8.314)(0.405)}{0.00274 \; \rm{K^{-1}} – 0.00268 \; \rm{K^{-1}}}\]
\[\\ = \dfrac{(3.37\; \rm{J\; mol^{–1} K^{–1}})}{5.87 \times 10^{-5}\; \rm{K^{–1}}} = 5740\; \rm{ J\; mol^{–1}} = 5.73 \; \rm{kJ \;mol^{–1}}\]
Comment: This low value seems reasonable because thermal denaturation of proteins primarily involves the disruption of relatively weak hydrogen bonds; no covalent bonds are broken (although disulfide bonds can interfere with this interpretation).
The pre-exponential factor
Up to this point, the pre-exponential term, A in the Arrhenius equation, has been ignored because it is not directly involved in relating temperature and activation energy, which is the main practical use of the equation.
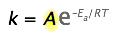
However, because A multiplies the exponential term, its value clearly contributes to the value of the rate constant and thus of the rate. Recall that the exponential part of the Arrhenius equation expresses the fraction of reactant molecules that possess enough kinetic energy to react, as governed by the Maxwell-Boltzmann law. This fraction can run from zero to nearly unity, depending on the magnitudes of \(E_a\) and of the temperature.
If this fraction were 0, the Arrhenius law would reduce to
\[k = A\]
In other words, \(A\) is the fraction of molecules that would react if either the activation energy were zero, or if the kinetic energy of all molecules exceeded \(E_a\) — admittedly, an uncommon scenario (although barrierless reactions have been characterized).
The Role of Collisions
What would limit the rate constant if there were no activation energy requirements? The most obvious factor would be the rate at which reactant molecules come into contact. This can be calculated from kinetic molecular theory and is known as the frequency- or collision factor, \(Z\).
In some reactions, the relative orientation of the molecules at the point of collision is important, so a geometrical or steric factor (commonly denoted by \(\rho\) (Greek lower case rho) can be defined. In general, we can express \(A\) as the product of these two factors:
\[A=Z\rho\]
Values of ρ are generally very difficult to assess; they are sometime estimated by comparing the observed rate constant with the one in which \(A\) is assumed to be the same as \(Z\). Usually, the more complex the reactant molecules, the lower the steric factors. The deviation from unity can have different causes: the molecules are not spherical, so different geometries are possible; not all the kinetic energy is delivered into the right spot; the presence of a solvent (when applied to solutions) and other factors (Figure \(\PageIndex{4}\)).
Contributors and Attributions
Stephen Lower, Professor Emeritus (Simon Fraser U.) Chem1 Virtual Textbook
- Wikipedia

