19.5: Standard Electrochemical Potentials
- Page ID
- 60806
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Standard Cell Potential
In the last section we saw how the cell potential could be related to Gibbs Free Energy:
\[\Delta G = -nRE_{Cell}\]
If at standard state conditions we have:
\[\Delta G^o_{redox \; rxn} = -nRE^o_{Cell}\]
We know from chapter 19 that there are thermodynamic tables of standard state free energies of formation \(\Delta G^o_f\) that can be used to calculate \(\Delta G^o_{rxn}\), and in this section we will learn how to create a table of standard state reduction potentials for half reactions, and use those to calculate Eocell. This table is similar to the activity series for oxidation half reactions (Section 3.6.1.1) we covered in general chemistry one, but is written as a reduction instead of an oxidation.
The challenge is how do we measure a potential, and what is zero potential? According to Coulomb's Law, zero potential would be when two charged particles are separated by infinity, which is not an attainable situation.
\[E=K\frac{q_1q_2}{r}\]
For a redox reaction to occur one species must be reduced (gain electrons) and the other species must be oxidized (lose electrons), it is thus physically impossible to measure the potential of a single electrode. But you can measure the difference between the potentials of two electrodes. This means the value of the difference does not depend on the definition of zero potential. Consider the Zinc/Copper voltaic cell.
\[Zn_{(s)} ∣ Zn^{2+}(aq, 1 M)∥Cu^{2+}(aq, 1 M) ∣ Cu (s)\;\;\; E°=1.1\; V \]
The difference between the zinc anode of the copper cathode of the zinc/copper voltaic cell does not depend on what the true zero value is, along as both copper and zinc are measured against the same zero value. This is analogous to the difference between the boiling and freezing point of water being being the same in the kelvin (373.15-273.15) and Celsius (100 - 0), as they both have the same scale, just different zero points (0 Kelvin is absolute zero, 0 Celsius is the normal freezing point of water).

At standard state conditions the cell potential is the oxidation potential of the oxidation half reaction in the anode (because that species is being oxidized) and the reduction potential of the reduction half reaction in the cathode (because that species is getting reduced).
The potential of any half reaction can be written as either a reduction or oxidation potential (by simply writing the equation in the opposite direction and switching the sign). We will use a subscript to indicate the type of potential (oxidation or reduction potential) and parenthesis to indicate which half reaction is being described.
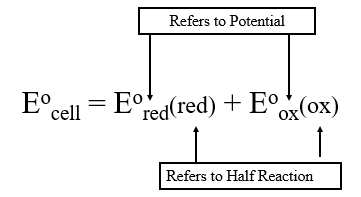
Since reduction is the opposite of oxidation, we can simply subtract the reduction potential of the oxidation half reaction.
Note:
Since \(\Delta G_{redox \; rxn} = -nRE_{Cell}\) we can see that if you reverse a reaction, the sign of the cell potential is reversed. This means the reduction potential of a half reaction is the negative of its oxidation potential
\[ \begin{align} E^o_{cell} & = E^o_{red}(red) \;+\;E^o_{ox}(ox) \\ & =E^o_{red}(red) \;-\;E^o_{red}(ox) \nonumber\end{align}\]
Simply add the reduction potential of the species being reduced and subtract the reduction potential of the species being oxidized.
In this class we will use the standard hydrogen reference electrode (SHE) and define its reduction potential as zero. If you find a table with different values, it is probably using a different standard electrode. There are situations where the SHE will simply not work, like non aqueous systems or when measuring transient (short-lived) chemicals that disappear before the SHE electrode achieves equilibrium.
Standard Hydrogen Electrode (SHE)
The following figure shows the basic structure of the SHE (Standard Hydrogen Electrode). This electrode may act as a cathode (reduction) or as an anode (oxidation). Note, at standard conditions the gas pressure is 1 atm and the hydronium ion concentration is 1 M. The platinum electrode is an inert electrode that does not get oxidized or reduced, but allows electrons to transfer between the aqueous and gaseous phases within the cell.
The standard potential of a reference electrode is 0 V, and we will write these as reduction potentials. So the standard reduction potential of the SHE is:
\[2H^+_{(aq)}+2e^− \rightleftharpoons H_{2(g)} \; \;\; \; V=0\]
Because it is impossible to measure the potential of any electrode directly, defining a reference electrode like the standard hydrogen electrode (SHE) as having zero potential allows us to measure the reduction potential of any other substance by measuring it against the SHE. When the SHE half cell is connected to another half cell, it may be the anode or the cathode, depending on which process is spontaneous. At standard conditions, any substance that spontaneously oxidizes hydrogen in the SHE has a positive reduction potential (it gets reduced) and the SHE is functioning as an Anode. Any substance at standard state that gets oxidized by hydrogen in the SHE has a negative reduction potential and the SHE functions as a Cathode. These different processes are described in the next section.
SHE as Anode
A galvanic cell consisting of a SHE and Cu2+/Cu half-cell can be used to determine the standard reduction potential for Cu2+ (Figure \(\PageIndex{1}\)), which is shown to have a voltage of 0.337V at standard state conditions.
In cell notation, the reaction is
\[\ce{Pt}(s)│\ce{H2}(g,\:1\: \ce{atm})│\ce{H+}(aq,\:1\:M)║\ce{Cu^2+}(aq,\:1\:M)│\ce{Cu}(s)\]
Electrons flow from the anode to the cathode. The reactions, which are reversible, are
&\textrm{Anode (oxidation): }\ce{H2}(g)⟶\ce{2H+}(aq) + \ce{2e-}\\
&\textrm{Cathode (reduction): }\ce{Cu^2+}(aq)+\ce{2e-}⟶\ce{Cu}(s)\\
&\overline{\textrm{Overall: }\ce{Cu^2+}(aq)+\ce{H2}(g)⟶\ce{2H+}(aq)+\ce{Cu}(s)}
\end{align*}\]
If a cell with the \(\ce{Cu(s)|Cu^{+2}(aq)}\) half reaction at standard conditions is connected to the SHE, the open circuit potential is 0.337V (Figure \(\PageIndex{4}\)).
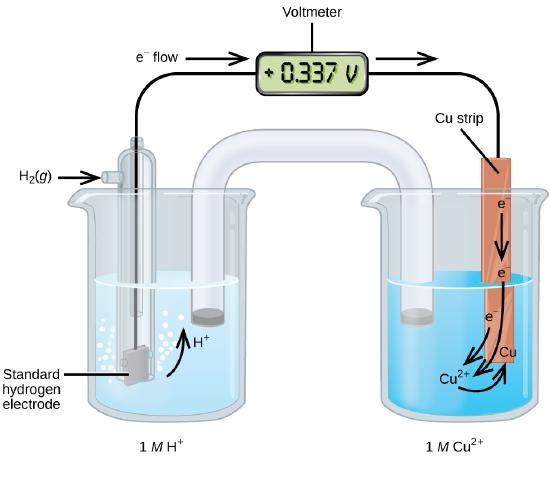
The standard reduction potential can be determined by subtracting the standard reduction potential for the reaction occurring at the anode from the standard reduction potential for the reaction occurring at the cathode. The minus sign is necessary because oxidation is the reverse of reduction.
\[E^\circ_\ce{cell}=\underbrace{E^\circ_\ce{cathode}−E^\circ_\ce{anode}}_{\text{all potentials are reduction potentials}}\]
\[\mathrm{+0.34\: V}=E^\circ_{\ce{Cu^2+/Cu}}−E^\circ_{\ce{H+/H2}}=E^\circ_{\ce{Cu^2+/Cu}}−0=E^\circ_{\ce{Cu^2+/Cu}}\]
Figure \(\PageIndex{2}\): A galvanic cell can be used to determine the standard reduction potential of Cu2+.
Remember, Oxidation occurs at the Anode and Reduction occurs at the cathode. The Reduction Potential of Cu+2 is Positive because it is getting reduced (the SHE is getting oxidized in the anode, but by definition, its potential is zero, and so we are measuring the reduction potential of copper.)
SHE as Cathode
A galvanic cell consisting of a SHE and Cu2+/Cu half-cell can be used to determine the standard reduction potential for Cu2+ (Figure \(\PageIndex{2}\)), which is shown to have a voltage of 0.337V at standard state conditions.
In cell notation, the reaction is
\[\ce{Zn}(s)│\ce{Zn^2+}(aq,\:1\:M)║\ce{H+}(aq,\:1\:M)│\ce{H2}(g,\:1\: \ce{atm})│\ce{Pt}(s)\]
Electrons flow from the anode to the cathode. The reactions, which are reversible, are
&\textrm{Anode (oxidation): }\ce{Zn}(s)⟶\ce{Zn^2+}(aq)+\ce{2e-}\\
&\textrm{Cathode (reduction): }\ce{2H+}(aq) + \ce{2e-}⟶\ce{H2}(g)\\
&\overline{\textrm{Overall: }\ce{Zn}(s)+\ce{2H+}(aq)⟶\ce{Zn^2+}(aq)+\ce{H2}(g)}
\end{align*}\]
If a cell with the \(\ce{Zn(s)|Zn^{+2}(aq)}\) half reaction at standard conditions is connected to the SHE, the open circuit potential is 0.76V (Figure \(\PageIndex{5}\)).

The standard reduction potential can be determined by subtracting the standard reduction potential for the reaction occurring at the anode from the standard reduction potential for the reaction occurring at the cathode. The minus sign is necessary because oxidation is the reverse of reduction.
\[E^\circ_\ce{cell}=\underbrace{E^\circ_\ce{cathode}−E^\circ_\ce{anode}}_{\text{all potentials are reduction potentials}}\]
\[\mathrm{+0.76\: V}=E^\circ_{\ce{H^+/H2}}-E^\circ_{\ce{Zn^2+/Zn}}=0-E^\circ_{\ce{Zn^2+/Zn}}=-E^\circ_{\ce{Zn^2+/Zn}}\]
therefor the reduction potential of zinc is
\[E^\circ_{\ce{Zn^2+/Cu}}=-0.76V\]
Remember, Oxidation occurs at the Anode and Reduction occurs at the cathode. The Reduction Potential of Zn+2 is Negative because it is getting oxidized (the SHE is getting reduced in the cathode, but by definition, its potential is zero, and so we are measuring the reduction potential of zinc.).
Standard Reduction Potential Tables
By selectively measuring different substance against the standard hydrogen electrode we can build a table of Reduction potentials that can then be used to calculate the standard state potential for any reaction from the standard reduction potential of the reductant and oxidant.
Note
LibreText gives you access to tables through the reference tab in the header of every webpage. There are two Standard reduction tables you can use: P1: Standard Reduction Potentials by Element and P2: Standard Reduction Potentials by Value
The following table is sorted by value.
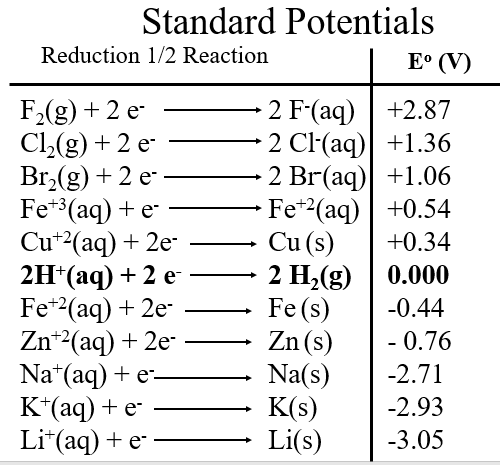
There are several things worth noting in Table \(\PageIndex{1}\). First, the highly electronegative fluorine has a very high reduction potential, meaning it tends to accept electrons, and likewise, its ion is very stable and does not want to lose electrons (fluoride's oxidation potential would b -2.87 V). Second, metals tend to lose electrons and so have very low oxidation potential, in fact many have negative reduction potentials, meaning they will give electrons to water).
Calculating Standard Reduction Potentials
With a table of reduction potentials you can calculate the Standard Reduction Potential for a chemical reaction. You note that in any redox reaction, one species must gain electrons (get reduced), while another loses electrons (gets oxidized). If you use the same standard state electrode (hydrogen in this class), the reduction potential for the reaction is the reduction potential of the cathode half reaction (where reduction occurs) minus that of the reduction potential of the anode half reaction (where oxidation occurs).
\[\ce{Zn}(s)│\ce{Zn^2+}(aq,\:1\:M)║\ce{Cu^2+}(aq,\:1\:M)│\ce{Cu}(s)\]
The overall reaction is:
\[E^\circ_\ce{cell}=\underbrace{E^\circ_\ce{cathode}−E^\circ_\ce{anode}}_{\text{all potentials are reduction potentials}}\]
\[E°_{cell} =.34V −.76V = 1.1V\]
Contributors and Attributions
Robert E. Belford (University of Arkansas Little Rock; Department of Chemistry). The breadth, depth and veracity of this work is the responsibility of Robert E. Belford, rebelford@ualr.edu. You should contact him if you have any concerns. This material has both original contributions, and content built upon prior contributions of the LibreTexts Community and other resources, including but not limited to:


