16.3: Equilibrium Constants for Acids and Bases
- Page ID
- 60742
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Introduction
In general chemistry 1 we calculated the pH of strong acids and bases by considering them to completely dissociate, that is, undergo 100% ionization. We will now look at weak acids and bases, which do not completely dissociate, and use equilibrium constants to calculate equilibrium concentrations. We could solve all these problems using the techniques from the last chapter on equilbria, but instead we are going to develop short cut techniques, and identify when they are valid. But first, we need to define what are equilibrium constants for acid base reactions.
Weak Acids
\[HA(aq)+H_2O(l)⇌H_3O^+(aq)+A^-(aq)\]
At first glance this gives an equilibrium constant of
\[K=\frac{[H_{3}O^{+}][A^{-}]}{[HA][H_{2}O]}\]
But we can consider the water concentration constant because it is much greater than of acid that has ionized. There are two factors at work here, first that the water is the solvent and so [H2O] is larger than [HA], and second, that [HA] is a weak acid, and so at equilibrium the amount ionized is smaller than [HA]. It should be noted that this is a homogenous equlibria, and although we are ignoring the water and treating it as a liquid, it is for a different reason than was used in the last chapter for heterogeneous equilibria.
This results in Acid Dissociation Constant (Ka) for aqueous systems:
\[K_{a}=\frac{[H_{3}O^{+}][A^{-}]}{[HA]}\]
where, \(K_a=K[H_2O]\)
Ka is only used for weak acids. Strong acids have a large Ka and completely dissociate and so you just state the reaction goes to completion.
Weak Bases
There are two types of weak bases, those as modeled by ammonia and amines, which grab a proton from water, and the conjugate bases of weak acids, which are ions, and grab the proton to form the weak acid.
Type 1:
\[B(aq) + H_2O(l) ⇌ HB^+(aq) + OH^-(aq)\]
Note, in this reaction the base removes a proton from the water and following the same logic for weak acids, we consider the water concentration to stay constant because only a small fraction of it reacts with the weak base, so:
\[K_b=\frac{[HB^+][OH^-]}{[B]}\]
An example of the first type would be that of methyl amine, CH3NH2.
\[CH_3NH_2(aq) + H_2O(l) ⇌CH_3NH_3^+(aq)+OH^- (aq) \\ \\ K=\frac{[CH_3NH_3^+][OH^-]}{[CH_3NH_2]} = 5.0x10^{-4}\]
Type 2:
\[A^-(aq) + H_2O(l) ⇌ HA(aq) + OH^-(aq)\]
\[K'_b=\frac{[HA][OH^-]}{[A^-]} \\ \text{ where} \; K_b \; \text{is the basic equilibrium constant of the conjugate base} \; A^- \; \text{of the weak acid HA}\]
Acid Base Conjugate Pairs
We will use K(a or b) to represent the acid or base equilibrium constant and K'(b or a) to represent the equilibrium constant of the conjugate pair.
For an Acid Base Conjugate Pair
\[\large K_aK_{b'}=K_w\]
Consider the generic acid HA which has the reaction and equilibrium constant of
\[HA(aq)+H_2O(l)⇌H_3O^+(aq)+A^-(aq), \; K_{a}=\frac{[H_{3}O^{+}][A^{-}]}{[HA]}\]
its conjugate base A- has the reaction and equilibrium constant of:
\[A^-(aq) + H_2O(l) ⇌ HA(aq) + OH^-(aq), K'_b=\frac{[HA][OH^-]}{[A^-]}\]
\[K_aK'_{b}=\left ( \frac{[H_{3}O^{+}] \textcolor{red}{\cancel{[A^{-}]}}}{ \textcolor{blue}{\cancel{[HA]}}}\right )\left (\frac{ \textcolor{blue}{\cancel{[HA]}}[OH^-]}{ \textcolor{red}{\cancel{[A^-]}}} \right )=[H_{3}O^{+}][OH^-]=K_w=10^{-14}\]
So there is an inverse relationship across the conjugate pair
- The Stronger an Acid the Weaker it's Conjugate Base
- The Weaker an Acid the Stronger it's Conjugate Base
- The Stronger the Base the Weaker it's Conjugate Acid
- The Weaker the Base the Stronger it's Conjugate Acid
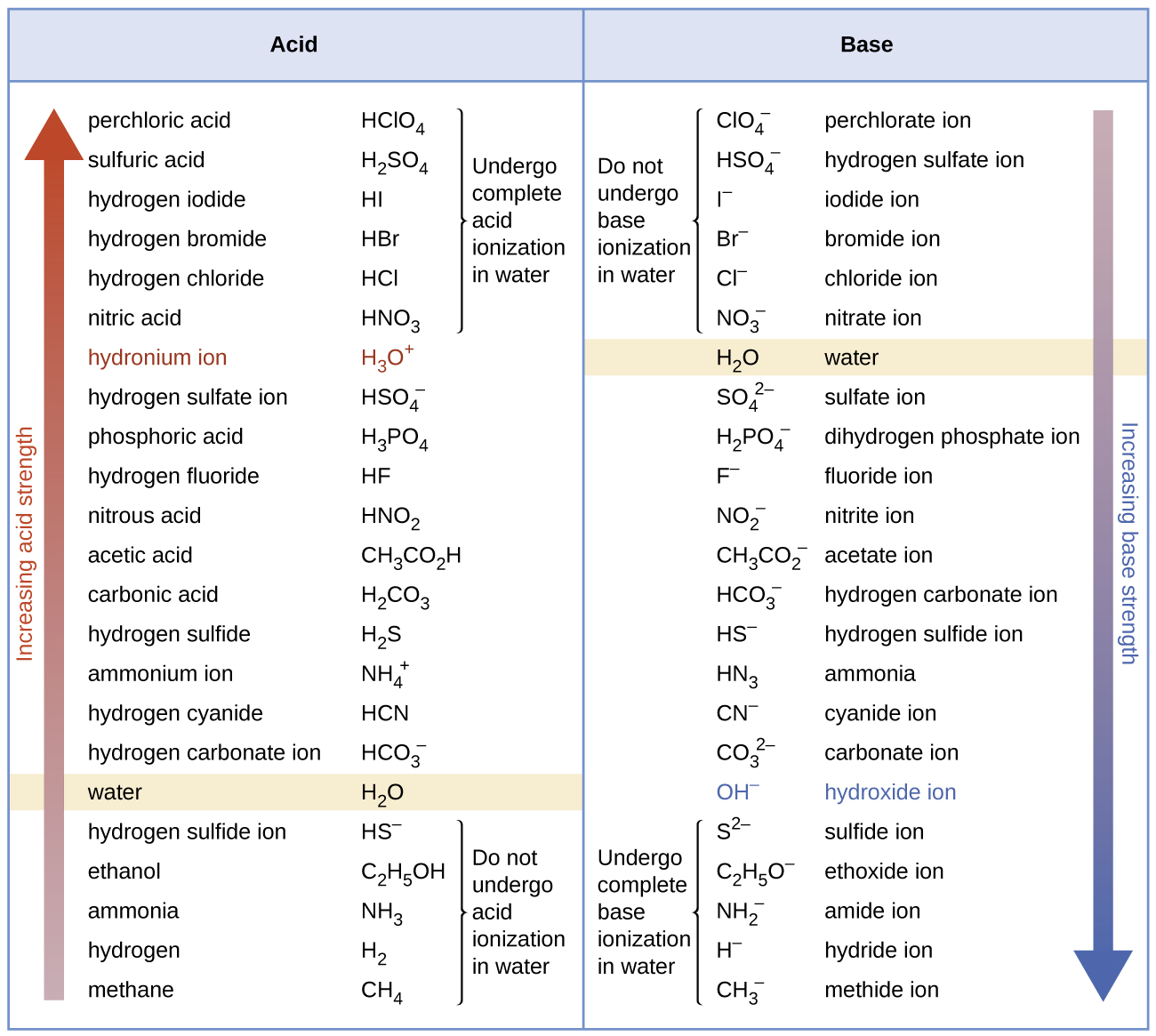
Figure\(\PageIndex{1}\): Relationship between acid or base strength and that of their conjugate base or acid.
Ka and Kb Values for PolyProtic Acids
PolyProtic Acids
It is always harder to remove a second proton from an acid because you are removing it from a negative charged species, and even harder to remove the third, as you are removing it from a dianion.
Consider a triprotic acid
\[H_3A + H_2O ⇌H_2A^- +H_3O^+ \; \; K_{a1}\]
\[H_2A^- + H_2O ⇌HA^{-2} +H_3O^+ \; \; K_{a2}\]
\[HA^{2}- + H_2O ⇌A^{-3} +H_3O^+ \; \; K_{a3}\]
\[K_{a1}>K_{a2}>K_{a3}\]
pKa and pKb
Because pKa and pKb values are so small they are often recorded a pX values, where pX= -logX. So
pKa = -logKa and Ka =10-pka
pKb = -logKb and Kb =10-pkb
Table of Ka
Table \(\PageIndex{1}\): Table of Acid Ionization Constants
| Name | Formula | Conjugate Base | K a1 | pKa1 | K a2 | pKa2 | K a3 | pKa3 | K a4 | pKa4 |
|---|---|---|---|---|---|---|---|---|---|---|
| Acetic acid | CH3CO2H | CH3CO2- | 1.75 × 10−5 | 4.756 | ||||||
| Arsenic acid | H3AsO4 | H2AsO4- | 5.5 × 10−3 | 2.26 | 1.7 × 10−7 | 6.76 | 5.1 × 10−12 | 11.29 | ||
| Benzoic acid | C6H5CO2H | C6H5CO2- | 6.25 × 10−5 | 4.204 | ||||||
| Boric acid | H3BO3 | H2BO3- | 5.4 × 10−10* | 9.27* | >1 × 10−14* | >14* | ||||
| Bromoacetic acid | CH2BrCO2H | CH2BrCO2- | 1.3 × 10−3 | 2.90 | ||||||
| Carbonic acid | H2CO3 | HCO3- | 4.5 × 10−7 | 6.35 | 4.7 × 10−11 | 10.33 | ||||
| Chloroacetic acid | CH2ClCO2H | CH2ClCO2- | 1.3 × 10−3 | 2.87 | ||||||
| Chlorous acid | HClO2 | ClO2- | 1.1 × 10−2 | 1.94 | ||||||
| Chromic acid | H2CrO4 | HCrO4- | 1.8 × 10−1 | 0.74 | 3.2 × 10−7 | 6.49 | ||||
| Citric acid | C6H8O7 | C6H7O7- | 7.4 × 10−4 | 3.13 | 1.7 × 10−5 | 4.76 | 4.0 × 10−7 | 6.40 | ||
| Cyanic acid | HCNO | HCNO- | 3.5 × 10−4 | 3.46 | ||||||
| Dichloroacetic acid | CHCl2CO2H | CHCl2CO2- | 4.5 × 10−2 | 1.35 | ||||||
| Fluoroacetic acid | CH2FCO2H | CH2FCO2- | 2.6 × 10−3 | 2.59 | ||||||
| Formic acid | CH2O2 | CHO2- | 1.8 × 10−4 | 3.75 | ||||||
| Hydrazoic acid | HN3 | N3- | 2.5 × 10−5 | 4.6 | ||||||
| Hydrocyanic acid | HCN | CN- | 6.2 × 10−10 | 9.21 | ||||||
| Hydrofluoric acid | HF | F- | 6.3 × 10−4 | 3.20 | ||||||
| Hydrogen selenide | H2Se | HSe- | 1.3 × 10−4 | 3.89 | 1.0× 10−11 | 11.0 | ||||
| Hydrogen sulfide | H2S | HS- | 8.9 × 10−8 | 7.05 | 1 × 10−19 | 19 | ||||
| Hydrogen telluride | H2Te | HTe- | 2.5 × 10−3‡ | 2.6‡ | 1 × 10−11 | 11 | ||||
| Hypobromous acid | HBrO | BrO- | 2.8 × 10−9 | 8.55 | ||||||
| Hypochlorous acid | HClO | ClO- | 4.0 × 10−8 | 7.40 | ||||||
| Hypoiodous acid | HIO | IO- | 3.2 × 10−11 | 10.5 | ||||||
| Iodic acid | HIO3 | IO3- | 1.7 × 10−1 | 0.78 | ||||||
| Iodoacetic acid | CH2ICO2H | CH2ICO2- | 6.6 × 10−4 | 3.18 | ||||||
| Nitrous acid | HNO2 | NO2- | 5.6 × 10−4 | 3.25 | ||||||
| Oxalic acid | C2H2O4 | C2HO4- | 5.6 × 10−2 | 1.25 | 1.5 × 10−4 | 3.81 | ||||
| Periodic acid | HIO4 | IO4- | 2.3 × 10−2 | 1.64 | ||||||
| Phenol | C6H5OH | C6H5O- | 1.0 × 10−10 | 9.99 | ||||||
| Phosphoric acid | H3PO4 | H2PO4- | 6.9 × 10−3 | 2.16 | 6.2 × 10−8 | 7.21 | 4.8 × 10−13 | 12.32 | ||
| Phosphorous acid | H3PO3 | H2PO3- | 5.0 × 10−2* | 1.3* | 2.0 × 10−7* | 6.70* | ||||
| Pyrophosphoric acid | H4P2O7 | H3P2O7- | 1.2 × 10−1 | 0.91 | 7.9 × 10−3 | 2.10 | 2.0 × 10−7 | 6.70 | 4.8 × 10−10 | 9.32 |
| Resorcinol | C6H4(OH)2 | C6H4O2H- | 4.8 × 10−10 | 9.32 | 7.9 × 10−12 | 11.1 | ||||
| Selenic acid | H2SeO4 | HSeO4- | Strong | Strong | 2.0 × 10−2 | 1.7 | ||||
| Selenious acid | H2SeO3 | HSeO3- | 2.4 × 10−3 | 2.62 | 4.8 × 10−9 | 8.32 | ||||
| Sulfuric acid | H2SO4 | HSO4- | Strong | Strong | 1.0 × 10−2 | 1.99 | ||||
| Sulfurous acid | H2SO3 | HSO3- | 1.4 × 10−2 | 1.85 | 6.3 × 10−8 | 7.2 | ||||
| meso-Tartaric acid | C4H6O6 | C4H5O6- | 6.8 × 10−4 | 3.17 | 1.2 × 10−5 | 4.91 | ||||
| Telluric acid | H2TeO4 | HTeO4- | 2.1 × 10−8‡ | 7.68‡ | 1.0 × 10−11‡ | 11.0‡ | ||||
| Tellurous acid | H2TeO3 | HTeO3- | 5.4 × 10−7 | 6.27 | 3.7 × 10−9 | 8.43 | ||||
| Trichloroacetic acid | CCl3CO2H | CCl3CO2- | 2.2 × 10−1 | 0.66 | ||||||
| Trifluoroacetic acid | CF3CO2H | CF3CO2- | 3.0 × 10−1 | 0.52 | ||||||
| * Measured at 20°C, not 25°C. | ||||||||||
| ‡ Measured at 18°C, not 25°C. | ||||||||||
Source of data: CRC Handbook of Chemistry and Physics, 84th Edition (2004).
Table of Kb
Table\(\PageIndex{2}\): Base Ionization Constants
| Name | Formula | \(K_b\) | \(pK_b\) | |
|---|---|---|---|---|
| Ammonia | NH3 | NH4+ | 1.8 × 10−5 | 4.75 |
| Aniline | C6H5NH2 | C6H5NH3+ | 7.4 × 10−10 | 9.13 |
| n-Butylamine | C4H9NH2 | C4H9NH3+ | 4.0 × 10−4 | 3.40 |
| sec-Butylamine | (CH3)2CHCH2NH2 | (CH3)2CHCH2H3+ | 3.6 × 10−4 | 3.44 |
| tert-Butylamine | (CH3)3CNH2 | (CH3)3CH3+ | 4.8 × 10−4 | 3.32 |
| Dimethylamine | (CH3)2NH | (CH3)2H2+ | 5.4 × 10−4 | 3.27 |
| Ethylamine | C2H5NH2 | C2H5NH3+ | 4.5 × 10−4 | 3.35 |
| Hydrazine | N2H4 | N2H5+ | 1.3 × 10−6 | 5.9 |
| Hydroxylamine | NH2OH | NH3OH+ | 8.7 × 10−9 | 8.06 |
| Methylamine | CH3NH2 | CH3NH3+ | 4.6 × 10−4 | 3.34 |
| Propylamine | C3H7NH2 | C3H7NH3+ | 3.5 × 10−4 | 3.46 |
| Pyridine | C5H5N | C5H6N+ | 1.7 × 10−9 | 8.77 |
| Trimethylamine | (CH3)3N | (CH3)3NH+ | 6.3 × 10−5 | 4.20 |
Source of data: CRC Handbook of Chemistry and Physics, 84th Edition (2004).
Weak Acid pH Calculations
We typically write the acid dissociation as:
\[HA \rightleftharpoons H^+ + A^- \]
Noting that water is omitted and hydronium is written as H+ (implicitly meaning H3O+ and not a free proton). This gives the following equilibrium constant
\[ K_a=\frac{[H^{+}][A^{-}]}{[HA]} \]
If we know K we can determine the pH or hydronium ion concentration using a rice diagram where we start with pure acid and measure determine how much dissociates.
| Reaction | \(HA\) | \(H^+\) | \(A^-\) |
|---|---|---|---|
| Initial | [HA]i | 0 | 0 |
| Change | -x | +x | +x |
| Equilibrium | [HA]i-x | x | x |
Noting that \(x=10^{-pH}\) (at equilibrium) and substituting, gives\[K_a =\frac{x^2}{[HA]_i-x}\]
Now by definition, a weak acid means very little dissociates and if x<< [HA]initial we can ignore the x in the denominator. The rule of thumb we will for this approximation is if [HA]initial >100Ka we will ignore x in the denominator and simplify the math
\[If \; [HA]_{i}>100K_a \\ \; \\ then \\ \; \\ [HA]_{i}-x \approxeq [HA]_{i} \\ \; \\ and \\ \; \\ K_a=\frac{x^2}{[HA]_{i}}\]
This allows us to avoid the quadratic equation and quickly solve for the hydronium ion concentration
\[ [H^+] =x =\sqrt{K_a[HA]_i}\]
and we can calculate pH for a weak acid
\[ pH=-log[H^+] = -log\sqrt{K_a[HA]_i}\]
Weak Base pH Calculations
A base reacts with water to accept a proton:
\[B + H_2O \rightleftharpoons BH^+ + OH^- \]
The water is omitted from the equilibrium constant expression giving.
\[ K_b=\frac{[BH^{+}][OH^{-}]}{[B]} \]
If we know K we can determine the pOH from the rice diagram, and once we know pOH, we can determine pH (because pH + pOH =14). So we follow a similiar calculation as that of the weak acid, but now we are calculating [OH-] and not [H+].
| Reaction | \(B\) | \(H_2O\) | \(BH^+\) | \(OH^-\) |
|---|---|---|---|---|
| Initial | [B]i | 0 | 0 | |
| Change | -x | +x | +x | |
| Equilibrium | [B]i-x | x | x |
Noting that \(x=10^{-pOH}\) (at equilibrium) and substituting, gives\[K_b =\frac{x^2}{[B]_i-x}\]
Now by definition, a weak base means very few protons are accepted and if x<< [B]initial we can ignore the x in the denominator. The rule of thumb we will for this approximation is if [B]initial >100Kb we will ignore x in the denominator and simplify the math
\[If \; [B]_{i}>100K_b \\ \; \\ then \\ \; \\ [B]_{i}-x \approxeq [B]_{i} \\ \; \\ and \\ \; \\ K_b=\frac{x^2}{[B]_{i}}\]
This allows us to avoid the quadratic equation and quickly solve for the hydroxide ion concentration
\[ [OH^-] =x =\sqrt{K_b[B]_i}\]
and we can calculate pOH for a weak acid
\[ pOH=-log[OH^-] = -log\sqrt{K_b[B]_i}\]
and now we can calculate pH
\[pH=14-pOH \\ \; \\ or \\ \; \\ pH=14+log\sqrt{K_b[B]_i}\]
Diprotic Acid pH Calculation
Consider a generic diprotic acid H2A, like carbonic acid, H2CO3. Remember that diprotic acids donate protons stepwise and there is an amphoteric intermediate HA-, so in the reaction of a diprotic acid there are 5 chemical species, H2A, HA-, A-2, H+ and OH-.
\[H_2A \rightleftharpoons H^+ + HA^- \;\;\;\;K_{1}=\frac{[H^+][HA^-]}{[H_2A]} \\ \; \\ HA^- \rightleftharpoons H^+ + A^{-2} \;\;\;\;K_{2}=\frac{[H^+][A^{-2}]}{[HA^-]}\]
From section 16.3.5 (Ka for polyprotic acids) and from table 16.3.1 (table of Ka) we see Ka1>>Ka2 and we can ignore the effect of the second dissociation on the hyrdonium ion concentration, so if [H2A]initial >100Ka1 we can use the weak acid approximation to solve for hydronium. Othewise we need to solve the quadratic equation
\[ [H^+] = [HA^-] = \sqrt{k_{a1}[H_2A]_i}\]
The H2A can now be determined
\[[H_2A] = H_2A]_i - [H^+]\]
From K2 we can calculate A-2 as [H+] = [HA-] and they cancel
\[K_2=\frac{\cancel{[H^+]}[A^{-2}]}{\cancel{[HA^-]}} \\ \; \\ so \\ \; \\ [A^{-2}]=K_2\]
and we can get hydroxide from the water ionization constant K_w
\[K_w=[H^+][OH^-] \\ \; \\ so \\ \; \\ [OH^-]=\frac{K_w}{[H^+]}\]
Percent Ionization and Dilution
Before completing this section we want to look at the effect of dilution on percent ionization and our rule of thumb that we can ignore the extent of dissociation when [HA]i>100Ka. For the generic acid:
\[HA \rightleftharpoons H^+ + A^- \\ \; \\ K_a=\frac{[H^{+}][A^{-}]}{[HA]} \]
We can write the RICE diagram
| Reaction | \(HA\) | \(H^+\) | \(A^-\) |
|---|---|---|---|
| Initial | [HA]i | 0 | 0 |
| Change | -x | +x | +x |
| Equilibrium | [HA]i-x | x | x |
noting that the amount ionized is x=[A-], where [A-] is the amount that formed the conjugate base.
So we can define the percent ionization of a weak acid as
\[\% I = \frac{[A^-]}{[HA]_i}(100)\]
Let's calculate the % Ionization of 1.0M and 0.01 M Acetic acid (Ka=1.8x10-5). Since both of these concentrations are greater than 100Ka, we will use the relationship
\[ [A^-]=[H^+]=\sqrt{K_a[HA]_i} \]
\[\% I = \frac{[A^-]}{[HA]_i}(100) = \frac{[\sqrt{K_a[HA]_i}]}{[HA]_i}(100)\]
For 1.0 M Acetic Acid
\[ \% I = \frac{\sqrt{1.8x10^{-5}[1.0]}}{[1.0]}(100) = 0.42%\]
For 0.01M Acetic Acid
\[ \% I = \frac{\sqrt{1.8x10^{-5}[0.01]}}{[0.01]}(100) = 4.2%\]
Note that as the solution becomes more dilute the percent ionization goes up, and the 0.01 M solution is barely greater than 100Ka , given less than 5% ionized, and our shortcut is saying this in negligible.
Now lets look at 0.0001M Acetic Acid. If we used the above formula we would get 42% ionized, and so x is not insignificant compared to the initial concentration and we would need to use the quadratic formula to solve the RICE diagram.
Robert E. Belford (University of Arkansas Little Rock; Department of Chemistry). The breadth, depth and veracity of this work is the responsibility of Robert E. Belford, rebelford@ualr.edu. You should contact him if you have any concerns. This material has both original contributions, and content built upon prior contributions of the LibreTexts Community and other resources, including but not limited to:


