14.1: Prelude
- Page ID
- 96776
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Introduction
Kinetics deals with the time evolution of a system that undergoes a change as it approaches equilibrium. Chemical kinetics is the branch of chemistry dealing with the rates of chemical reactions, that is, how fast they proceed. If a system is at equilibrium, there appears to be no reaction occurring on a macroscopic scale. If a reaction is occurring, the system is in a non-equilbrium state, and kinetics is the study of how it evolves over time until equilibrium is achieved. The next chapter will describe systems in equilibrium.
An easy to understand system can be described by the heat transfer from a hot object to a cold object. The hot object cools and the cold object warms until the reach the same temperature, Tequilibrium. At this point, heat is still being transferred, but the rate between the two objects is the same, and so the temperature does not change.
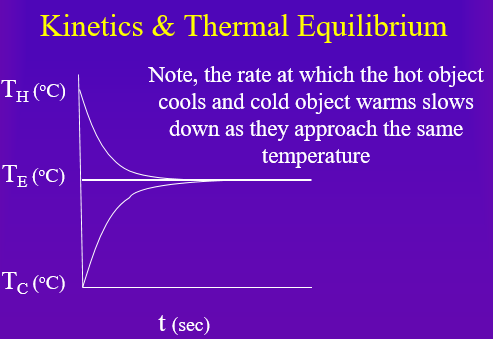
Calculus is the mathematics that studies how variables change with respect to each other, and kinetics is the study of how something changes with respect to time. In chemical kinetics it is the change of the concentration with respect to time. Figure \(\PageIndex{1}\) shows the kinetics of temperature change as heat is transferred from a hot object to a cold object. The instantaneous slope of the line is called the derivative, and represents the rate of temperature change. Figure \(\PageIndex{1}\) is of interest, because the rate of temperature change is related to the temperature difference. The greater the temperature difference, the faster the rate of change, and as the temperatures of the hot and cold objects approach the same temperature, the slower the rate of change. From calculus, such a dependency results in an exponential/logarithmic relationship, and it is because of this that chemical kinetics often shows exponential relationships that require students to master logarithms. That is, the rate of many chemical reactions depend on the concentration of the chemical, and this often requires students to be able to use both power functions (f(x)=Axm) and exponential functions (f(x)=Aemx), and their logarithmic relationships.
You need to be familiar with the following relationships
Math Review
Exponentials and Logarithims
102=100 log10100 = 2
Relationships in Base-10 Logarithms
| Numerical Value | Exponential Form | Logarithm |
|---|---|---|
| 100 | 102 | 2 |
| 10 | 101 | 1 |
| 1 | 100 | 0 |
| 0.1 | 10−1 | −1 |
| 0.01 | 10−2 | −2 |
Comparing logarithms to scientific notation
Video \(\PageIndex{1}\): 3:07 YouTube relating logarithms to scientific notation (https://youtu.be/i9K9fIF__6g)
Note, the log of a number between 1 and 10 is a fraction, and an easy way to understand logarithms is to relate them to scientific notation.
Let’s consider the number 26794
It can be expressed in scientific notation or as a log
So logarithms are very similar to scientific notation, where the number being multiplied by 10 to a power is expressed as 10 to the power of a fraction.
You are required to know these operations.
If the above do not make sense to you, try doing them with base 10, or base 2, but something you can do off your head:
Video \(\PageIndex{2}\): 4:59 YouTube on manipulating logarithms (https://youtu.be/NP0PAJlmnkg)
For example if aman = a(m+n) makes no sense to you,
try it with base 10.
102x103 = 10(2+3) = 105 = 100,000
Exercise \(\PageIndex{1}\)
Show that aman = a(m+n) using base 10, with m=2 and n=3
and then
logxy = logx +logY for X=100 and Y=1000
- Answer
-
102x103 = 10(2+3) = 105 = 100,000
(ie., a hundred times a thousand is a hundred thousand)
and
log[(100)(1000) = log(100) + log(1000)
log[(100,000) = log(100) + log(1000
5 = 2 + 3
In Class Activities
ADAPT \(\PageIndex{1}\)
Test Yourself
Homework: Section 14.1
Query \(\PageIndex{1}\)
Robert E. Belford (University of Arkansas Little Rock; Department of Chemistry). The breadth, depth and veracity of this work is the responsibility of Robert E. Belford, rebelford@ualr.edu. You should contact him if you have any concerns. This material has both original contributions, and content built upon prior contributions of the LibreTexts Community and other resources, including but not limited to:
- Liliane Poirot

