11.0: Prelude
- Page ID
- 407791
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Introduction:
In this chapter we are going to look at intermolecular forces, the forces "between molecules", and the liquid state (phase) of matter. Before this we should review some of the fundamentals of so called "Intramolecular forces", those within a molecule. So far we have looked at 4 basic types of chemical bonds:
- Ionic Bonds (resulting from coulombic interactions of positive cations with negative anions)
- Covalent Bonds (resulting by the sharing of valence electrons in orbitals that involve two or more nuclei)
- Polar Covalent Bonds (covalent bonds involving non-equal sharing of electrons by multiple nuclei)
- Metallic Bonds (these have only been mentioned, and will be covered in chapter 12, but they are different than the above)
In section 8.1 Chemical Bond Formation, we introduced the Arkel-Ketelaar diagram to identify which type of bond occurs as a result of :
- The average electronegativity (\(\chi\) )of the bonding atoms (x-axis).
- metals have low values (0.7-2.0ish), alloys are metallic compounds
- Nonmetals have high values (2.5-4), molecules are compounds of nonmetals
- The difference (\(\Delta \chi\)) in electronegativities (y-axis).
- \(\Delta \chi\)<0.5, covalent or metallic compound (covalent if high \(\chi\), and metallic if low \(\chi\)\)
- 0.5<\(\Delta \chi\)<2.0, polar covalent
- \(\Delta \chi\)>2.0, ionic (between metal (low \(\chi\)) and nonmetal (high \(\chi\))
(Note: these values are "Rule of Thumb" values)
Figure 11.0.1: Van Arkel-Ketelaar diagram showing what type of bond will occur between two atoms. (Remember, due to symmetry polar bonds can result in nonpolar molecules and here we are just talking about bonds).
Chemical bonds are the result of coulombic interactions between charged particles, where like charges repel and opposite charges attract. In the case of covalent bonds, these are between electrons and the nuclei of one atom with the electrons and nuclei of another. In the case of ionic bonds, these are between cations and anions. Coulombic interactions can be described by Coulomb's Law:
\[ E=k \dfrac{q_1q_2}{r} \; \; \; \; \; \; \; \; F= k\dfrac{q_1q_2}{r^2}\]
- E is the potential energy
- F is the force
- k is a proportionality constant
- in a vacuum \(k=\frac{1}{4\pi \epsilon _{o}}\)
- r is the distance of separation (note that the potential goes to zero when they are separated by infinity)
- q is the charge of the ions
It is important to note that a negative potential correlates to a bond. This is a consequence of the First Law of Thermodynamics and can be understood by looking at the Quick Review on the Covalent Bond and the Potential Well. What you realize is that zero potential correlates to r approaching infinity (the ions are too far away to interact), and that from the first law of thermodynamics, positive energy correlates to adding energy to the system. To break a bond you must add energy, and if the broken bond equates to zero energy, the bond energy must be negative. This makes complete sense when you look at the potential well diagram.
Quick Review: Covalent Bond and Potential Well
Covalent bonds were introduced in sections 2.5 (Chemical Compounds) and 9.2 (Valence Bond Theory) of the first semester class, where a bond occurs when electrons on one atom become attracted to the nucleus of the other atom and these interactions can be described by the potential well. Figure \(\PageIndex{2}\) is the potential well for diatomic hydrogen, and it should be noted that there are both are both attractive and repulsive Coulombic interactions, which result in a dynamic oscillation type of bond (see Video 2.5.1).
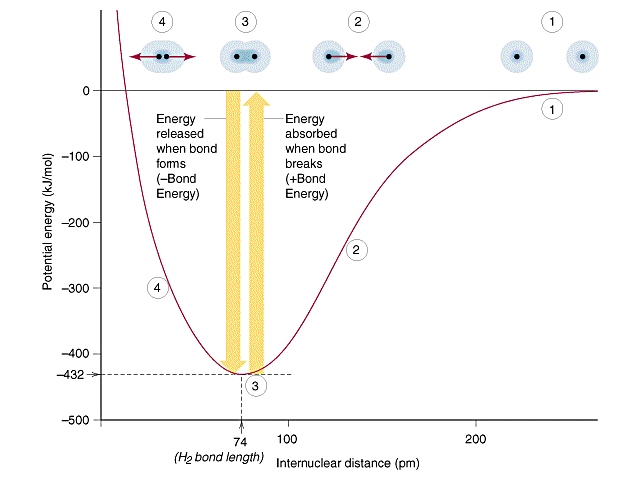
In this diagram there are 4 regions of the potential well.
Region 1 - Zero Interactions: When the two H atoms are separated by great distance the bond interaction is zero (the denominator of Coulomb's law is so large the value approaches zero).
Region 2 - Net Attractive Interactions: As the atoms come closer together the valence electrons of one atom are attracted to the nucleus of the other, with a net attractive force, that overcomes the nuclear-nuclear and electron-electron repulsion.
Region 3 - Oscillating Bond: The "bond length" and bond energy are described by the bottom of the curve (see Video 2.5.1) as the bond oscillates between the net attractive forces of region 2 with the net repulsive forces of region 4.
Region 4 - Net Repulsive Interactions: As the atoms get closer to each other nuclear-nuclear and electron-electron repulsions start to dominate.
Key Points
- Bond energies of Coulombic in nature.
- This is important as "intermolecular" forces are also Coulombic in nature.
- Bonds are at a lower energy than the separated atoms
- Bond energies can be described as either:
- Formation Energies (exothermic processes)
- Energy is released to form a bond
- Dissociation Energies (endothermic processes
- Energy is consumed to break a bond
- Formation Energies (exothermic processes)

