12: Solids

Prelude

 

 

Crystal Lattices and Unit Cells

Exercise \(\PageIndex{2a}\)

Crystalline solids differ from amorphous solids by _____.

1. Substantial intermolecular attractive forces
2. A long-range repeating pattern of atoms, molecules, or ions
3. Atoms, molecule, or ions that are close together
4. Much larger atoms, molecules, or ions
5. No orderly structure

Answer

b. A long-range repeating pattern of atoms, molecules, or ions 

Exercise \(\PageIndex{2b}\)

______ is a unit cell with all sides the same length and all angles equal to 90° that has lattice points only at the corners.

1. Body-centered cubic
2. Face-centered cubic
3. Monoclinic
4. Primitive cubic
5. Spherical cubic

Answer

d. Primitive cubic

Exercise \(\PageIndex{2c}\)

What is the fraction that each corner atom takes up in a face-centered cubic unit cell?

1. 1
2. 1/2
3. 1/4
4. 1/8
5. 1/16

Answer

d. 1/8

Exercise \(\PageIndex{2d}\)

A face-centered cubic unit cell contains how many atoms?

Answer

Four

Exercise \(\PageIndex{2e}\)

Based on sodium chloride structure, which of the following cannot form a solid lattice?

1. NaBr
2. LiF
3. RbI
4. CuO
5. CuCl₂

Answer

e. CuCl₂

Exercise \(\PageIndex{2f}\)

 What type of solid is held together by dispersion, dipole-dipole or hydrogen bonds?

1. Ionic
2. metallic
3. molecular
4. covalent network

Answer

c. molecular

Exercise \(\PageIndex{2g}\)

What type of compounds are held together by covalent bonds? (there can be more than one correct answer)

1. ionic
2. metallic
3. molecular
4. covalent network

Answer

d. covalent network and molecular

Exercise \(\PageIndex{2h}\)

Solid Iodine is a ____type of substance:

1. ionic lattice
2. metallic
3. molecular
4. covalent network

Answer

c. molecular

Exercise \(\PageIndex{2i}\)

Diamond lattices are a ___ type of substance

1. ionic crystal
2. metallic
3. molecular
4. network covalent

Answer

d. network covalent

Exercise \(\PageIndex{2j}\)

How many basic crystal systems are there?

1. 3
2. 4
3. 6
4. 7

Answer

d. 7

Exercise \(\PageIndex{2k}\)

Which is not a type of cubic unit cell?

1. tetragonal
2. body-centered
3. face centered
4. primitive

Answer

a. tetragonal

Exercise \(\PageIndex{2l}\)

Which type of cubic unit cell is the least efficient in packing?

1. primitive
2. body-centered
3. face-centered
4. none of the above

Answer

a. primitive

Exercise \(\PageIndex{2m}\)

Which type of cubic unit cell is most efficient in packing?

1. primitive
2. body-centered
3. face-centered
4. none of the above

Answer

c. face-centered

Exercise \(\PageIndex{2n}\)

Primitive, Face-Centered & Body-Centered Cubic Cells have respective coordination numbers of

1. 1,2,4
2. 2,4,6
3. 6,8,12
4. 6,12,8

Answer

d. 6,12,8

 

Exercise \(\PageIndex{2o}\)

In a face-centered cubic cell, what portion of the volume of each atom or ion on the face of a unit is within the unit cell?

Answer

1/2 of the atom is within the unit cell

Exercise \(\PageIndex{2p}\)

Gallium crystallizes in a primitive cubic unit cell. What is the radius of the Ga atom in Angstroms if the length of the unit cell edge is 3.70Å?

Answer

\[l=2r\]

\[r=\frac{l}{2}=\frac{3.70\AA }{2}=1.85 \AA\] 

Exercise \(\PageIndex{2q}\)

Potassium metal crystallizes in a body-centered cubic unit cell. What is the radius of the K atom in Angstroms if the length of the unit cell edge is 5.31 Å?

Answer

\[b^{2}=a^{2}+a^{2}\]

\[b=\sqrt{2a^{2}}=\sqrt{2*(5.31)^{2}}=7.51\AA\]

\[c^{2}=a^{2}+b^{2}\

\[c=\sqrt{a^{2}+b^{2}}=\sqrt{(5.31)^{2}+(7.51)^{2}}=9.20\AA\]

\[c=4r\]

\[r=\frac{c}{4}=\frac{9.20\AA }{4}=2.30\AA\]

Exercise \(\PageIndex{2r}\)

What is the radius of a copper atom in Angstroms if the length of the unit cell edge is 5.34Å? Copper has a face-centered cubic structure.

Answer

\[c^{2}=a^{2}+a^{2}\]

\[c=\sqrt{2a^{2}}=\sqrt{2*\left ( 5.34\AA \right )^{2}}=7.55 \AA \]

\[r=\frac{c}{4}=\frac{7.55\AA }{4}=1.89 \AA \]

Exercise \(\PageIndex{2s}\)

Silver has a density of 10.5g/cm³ and forms an FCC structure. What is the atomic radius of silver in Angstroms? Assume that nearest-neighbor atoms contact each other.

Answer

1. Calculate volume of unit cell

\[\left ( \frac{4\,atoms}{unit\,cell} \right )\left ( \frac{1\,mol}{6.022*10^{23}\,atoms} \right )\left ( \frac{107.87\,g}{1\,mol} \right )\left ( \frac{1\,cm^{3}}{10.5\,g} \right )=6.82*10^{-23}\,cm^{3}\]

2. Calculate length of unit cell

\[V=l^{3}\]

\[l=\sqrt[3]{V}\]

\[l=\sqrt[3]{V}=\sqrt[3]{6.82*10^{-23}cm^{3}}=4.09*10^{-8}cm*\left ( \frac{10^{10}\AA }{100cm} \right )=4.09\AA\]

3. Calculate radius of unit cell

\[c^{2}=a^{2}+a^{2}\]

\[c=\sqrt{2a^{2}}=\sqrt{2*\left ( 4.09\AA \right )^{2}}=5.78\AA\]

\[r=\frac{c}{4}=\frac{5.78\AA }{4}=1.44\AA\]
 

Exercise \(\PageIndex{2t}\)

An unknown element has a density of 11.07g/mL and forms a Simple Cubic Cell. What is the atomic radius of the unknown element in Angstroms? (unknown element has molar mass of 207.2g/mol)

Answer

1. Calculate volume of unit cell

\[\left ( \frac{1 atom}{unit cell} \right )\left ( \frac{1 mol}{6.022*10^{23}atoms} \right )\left ( \frac{207.2g}{1mol} \right )\left ( \frac{1mL}{11.07g} \right )=3.11*10^{-23}cm^{3}\]

2. Calculate length of unit cell

\[V=l^{3}\]

\[l=\sqrt[3]{V}\]

\[l=\sqrt[3]{V}=\sqrt[3]{3.11*10^{-23}cm^{3}}=3.14*10^{-8}cm*\left ( \frac{10^{10}\AA }{100cm} \right )=3.14\AA\]

3. Calculate radius of unit cell

\[l=2r\]

\[r=\frac{l}{2}=\frac{3.14\AA }{2}=1.57\AA\] 

Exercise \(\PageIndex{2u}\)

Tungsten has a density of 19.25g/cm3 and forms a BCC structure. What is the atomic radius of tungsten in Angstroms?

Answer

1. Calculate volume of unit cell

\[\left ( \frac{2\,atoms}{unit\,cell} \right )\left ( \frac{mol}{6.022*10^{23}\,atoms} \right )\left ( \frac{183.94\,g}{mol} \right )\left ( \frac{1\,cm^{3}}{19.25\,g} \right )=3.17*10^{-23}\,cm^{3}\]

2. Calculate length of unit cell

\[V=l^{3}\]

\[l=\sqrt[3]{V}\]

\[l=\sqrt[3]{V}=\sqrt[3]{3.17*10^{-23}cm^{3}}=3.17*10^{-8}cm*\left ( \frac{10^{10}\AA }{100cm} \right )=3.17\AA=a\]

3. Calculate radius of unit cell

\[b^{2}=a^{2}+a^{2}\]

\[b=\sqrt{2a^{2}}=\sqrt{2*(3.17)^{2}}=4.48\AA\]

\[c^{2}=a^{2}+b^{2}\]

\[c=\sqrt{a^{2}+b^{2}}=\sqrt{(3.17)^{2}+(4.48)^{2}}=5.49\AA\]

\[c=4r\]

\[r=\frac{c}{4}=\frac{5.49\AA }{4}=1.37\AA\]

Ionic Solids

 

Bonding in Metals and Semiconductors

 

Network and Amorphous Solids

 

Phase Diagrams

Exercise \(\PageIndex{6a}\)

A substance under normal conditions would rather sublime than melt if _____.

1. Its critical point occurs at a pressure above atmospheric pressure
2. Its critical point occurs at a temperature above room temperature
3. Its critical temperature is above its normal boiling point
4. Its triple point occurs at a pressure above atmospheric pressure
5. Its triple point occurs at a pressure below atmospheric pressure

Answer

d. Its triple point occurs at a pressure above atmospheric pressure 

Exercise \(\PageIndex{6b}\)

If a phase diagram has a solid-liquid phase boundary line that has a negative slope (leans to left) the substance,

1. Can go from solid to liquid, within a small temperature range, via the application of pressure
2. Cannot be liquefied above its triple point
3. Cannot go from solid to liquid by application of pressure at any temperature
4. Melts rather than sublimes under ordinary conditions
5. Sublimes rather than melts under ordinary conditions

Answer

a. Can go from solid to liquid, within a small temperature range, via the application of pressure

Exercise \(\PageIndex{6c}\)

The critical temperature, on a phase diagram, is _____.

1. The temperature above which a gas cannot be liquefied
2. The temperature at which all these states are in equilibrium
3. The temperature below which a gas cannot be liquefied
4. The temperature required to cause sublimation of a solid
5. The temperature required to melt a solid

Answer

a. The temperature above which a gas cannot be liquefied

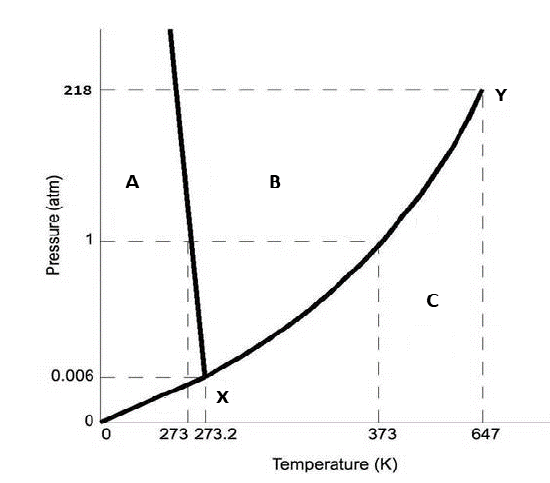
Figure 12.7.1: Use this figure to answer the following questions.

Exercise \(\PageIndex{6d}\)

The point X represents

1. the critical point, where a solid, liquid and vapor can coexist
2. The critical point where the two fluid phases cannot be distinguished
3. The triple point, where a solid, liquid and vapor can coexist
4. The triple point, where the fluid phases cannot be separated

Answer

c. The triple point, where a solid, liquid and vapor can coexist

Exercise \(\PageIndex{6e}\)

The point Y in the figure represents

1. the critical point, where a solid, liquid and vapor can coexist
2. The critical point where the two fluid phases cannot be distinguished
3. The triple point, where a solid, liquid and vapor can coexist
4. The triple point, where the fluid phases cannot be separated

Answer

b. The critical point where the two fluid phases cannot be distinguished

Exercise \(\PageIndex{6f}\)

Region A of the figure represents

1. solid
2. liquid
3. vapor
4. none of the above

Answer

a. solid

Exercise \(\PageIndex{6g}\)

Region B of the figure represents

1. solid
2. liquid
3. vapor
4. none of the above

Answer

b. liquid

Exercise \(\PageIndex{6.8}\)

Region C of the figure represents

1. solid
2. liquid
3. vapor
4. none of the above

Answer

c. vapor

Exercise \(\PageIndex{6h}\)

The negative slope between regions A and B of figure 12.7.1 indicates:

1. the solid is denser than the liquid
2. the liquid is denser than the solid
3. the vapor is denser than the liquid
4. the vapor is denser than the solid

Answer

b. the liquid is denser than the solid

Exercise \(\PageIndex{6i}\)

Figure 12.7.1 is consistent with a phase diagram for which compound

1. carbon dioxide
2. sodium
3. water
4. carbon dioxide and water

Answer

c. water

Exercise \(\PageIndex{6j}\)

The compound in figure 12.7.1 sublimes at pressures:

1. greater than deg O°C
2. Pressures greater than 1.0 atm
3. pressures between 0.0060 and 1.00 atm
4. pressures less than 0.0060 atm

Answer

d. pressures less than 0.0060 atm

Exercise \(\PageIndex{6k}\)

Consider a 1 atm isobar for the compound in figure 12.7.1. Moving left to right in region A represents

1. freezing
2. melting
3. heating supercooled ice
4. none of the above

Answer

c. heating supercooled ice

Exercise \(\PageIndex{6l}\)

Consider a 1 atm isobar for the compound in figure 12.7.1. Adding heat to a substance in region A causes it to warm, what happens when you reach the line between region A & B?

1. it boils
2. it melts
3. it freezes
4. it continues to warm up

Answer

b. it melts

Exercise \(\PageIndex{6m}\)

Consider a 1 atm isobar for the compound in figure 12.7.1. Moving left to right in region B represents

1. melting
2. boiling
3. heating liquid water
4. cooling liquid water

Answer

c. heating liquid water

Exercise \(\PageIndex{6n}\)

Consider a 1 atm isobar for the compound in figure 12.7.1. Adding heat to a substance in region B causes it to warm, what happens when you reach the line between region B & C?

1. it continues to warm
2. it condenses
3. it boils
4. all of the above

Answer

c. it boils

Exercise \(\PageIndex{6o}\)

Consider a 1 atm isobar for the compound in figure 12.7.1. Moving left to right in region C represents

1. cooling water
2. heating liquid water
3. heating ice
4. heating steam

Answer

d. heating steam

Exercise \(\PageIndex{6p}\)

At what pressure can liquid, solid and gaseous water coexist?

1. 218 atm
2. 1.00 atm
3. 0.0060 atm
4. none of the above

Answer

c. 0.0060 atm

Figure 12.7.2: Use this phase diagram to answer the following questions.

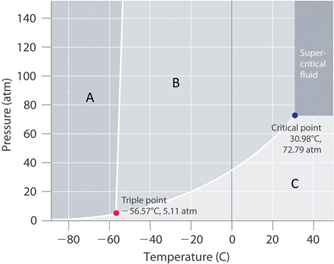
Exercise \(\PageIndex{6q}\)

Consider a -50°C isotherm for the compound in Figure 12.7.2. Moving from region A to C represents

1. Condensation then Freezing
2. Freezing then Condensation
3. Melting then Vaporizing
4. Vaporizing then Melting

Answer

c. Melting then Vaporizing

Exercise \(\PageIndex{6r}\)

Consider a 5 atm isobar for the compound in Figure 12.7.2. Moving from region C to A represents

1. Condensation
2. Deposition
3. Sublimation
4. Vaporization

Answer

b. Deposition

Exercise \(\PageIndex{6s}\)

What phase would this compound be in if the pressure and temperature were at room conditions?

Answer

This substance would be a gas

Exercise \(\PageIndex{6t}\)

The positive slope between regions A and B of figure 12.7.2 indicates:

1. the solid is denser than the liquid
2. the liquid is denser than the solid
3. the vapor is denser than the liquid
4. the vapor is denser than the solid

Answer

a. the solid is denser than the liquid

Exercise \(\PageIndex{6u}\)

Figure 12.7.2 is consistent with a phase diagram for which compound

1. Carbon dioxide
2. Carbon dioxide and water
3. Sodium
4. Water

Answer

a. Carbon dioxide