8.7: Bond Polarity and Electronegativity (\(\chi\))
- Page ID
- 52693
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Introduction
In a covalent bond electrons are shared in a bonding orbital between two nuclei. If it is a homonuclear bond (between atoms of the same element like in H2, N2, O2, Cl2,...), the bonding electrons are shared equally and the charge distribution around the bond is symmetric (left animation of Figure \(\PageIndex{1}\)). If it is a heteronuclear bond like H-Cl or H-C, the electrons may or may not be shared equally. Equally shared electrons result in a non-polar bond and unequally shared electrons result in a polar bond, where one atom feels a partially positive charge (\(\delta ^{+}\)) and the other atom feels a partially negative charge (\(\delta ^{-}\)). In this Chapter we will introduce the concept of electronegativity (\(\chi\), pronounced "ky" as in "sky") to help identify if a bond is polar or not. In a bond with atoms of different electronegativity, the bonding atoms with a higher electronegativity attracting electron density more than atoms with a lower electronegativity, and so it has a partially negative charge..
 |
 |
| Orbitals of two atoms of similar electronegativity come together to form a symmetric nonpolar covalent bond | Orbitals of two atoms of dissimilar electronegativity come together and form an asymmetric polar covalent bond. |
Figure \(\PageIndex{1}\) : The atoms of the left have equal electronegativity and so form a nonpolar bond with a symmetric electron distribution. The atoms on the right have different electronegativity, with the pink orbital having a higher electronegativity than the blue, and so the resulting bond is asymmetric, with there being a partial negative charge on the more electronegative atom and a partial positive on the less electronegative atom.
In Summary:
- A nonpolar covalent bond has a symmetric bonding orbital electron density function with equal sharing of the bonding electron.
- A polar covalent bond has an asymmetric bonding orbital electron density function with non-equal sharing of the bonding electrons
Electronegativity
Introduction
Electronegativity is not a thermodynamic property and has no units. The term "electronegativity" was introduced by Berzelius in 1811 and we will use the Pauling scale for electronegativities, developed by Linus Pauling, which ranges in value from 0.7 (Francium and Cesium) to 4.0 (Fluorine). Although we assign electronegativity values to element, they are not properties of an atoms per se, but of the atoms when in a bond. That is, if two atoms of different electronegativities form a bond, the more electronegative element will pull electron density from the less electronegative element, which can also be classified as the more electropositive element. It also needs to be noted that in a molecule where an atom is bonded to more than one other atom, the actual electron distribution is the result of all interactions.
Periodic Trends of Electronegativities
On a basic level, electronegativities can be correlated to ionization energies and electron affinities, although the later are thermodynamic properties of an isolated atom in the gas phase, while electronegativities are based on an arbitrary unitless scale. That said, atoms with low ionization energies (which are always endothermic) tend to be electropositive, because they do not tightly hold onto their valence electrons. Likewise, atoms with exothermic electron affinities (release energy when they gain an electron) tend to have high electron energies as they like to gain electrons.
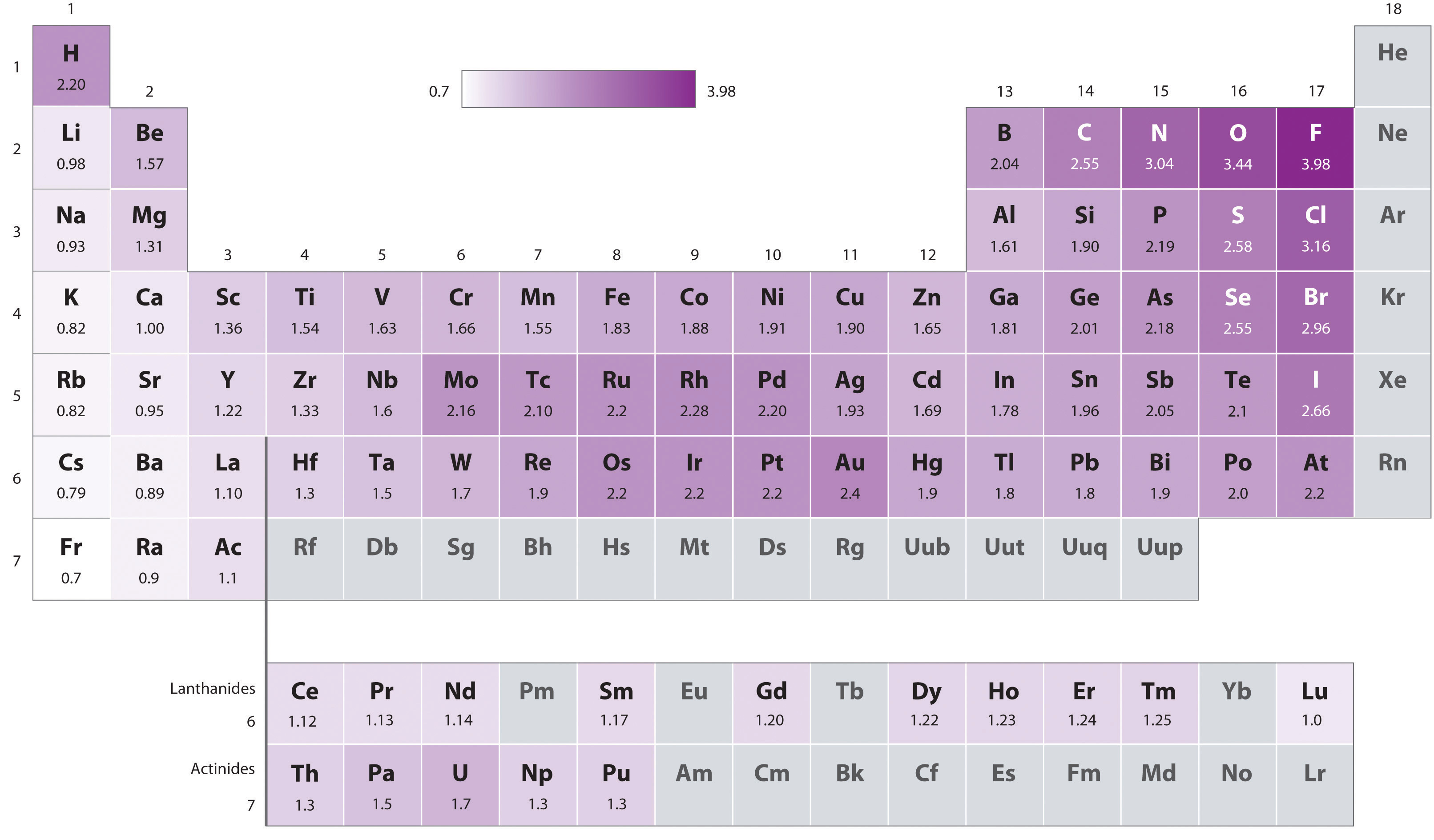
Exercise \(\PageIndex{1}\)
Why do the Noble Gases in Table 8.7.1 not have a value for electronegativity?
- Answer
- Remember, electronegativity is not a thermodynamic property, but a relative value given to an atom in a bond, which indicates how strongly it pulls the shared electron density towards itself. The noble gasses tend to not bond with other elements, which is why we call them noble, and thus it does not make sense to give them a value.
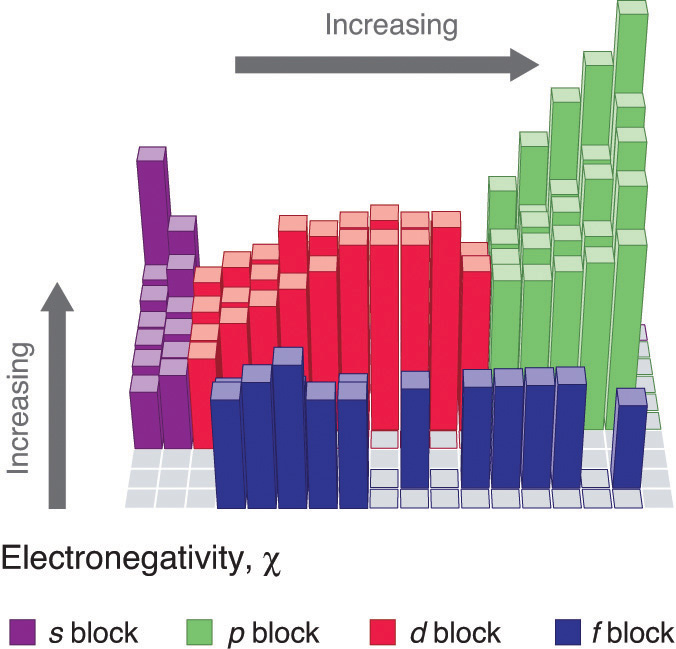
Figure \(\PageIndex{3}\): Diagram showing periodic trends in electronegativity. Note going up a group and across a period results in an increase in electronegativity.
Exercise \(\PageIndex{2}\)
Why would going across (left to right) a period result in an increase in electronegativity?
- Answer
-
Remember that the effective nuclear charge increases going across a period, and the size of the atoms get smaller. This means the pull on the electron would be stronger, and so the trend makes sense.
Why would going down a group result in increased electropositivity (decreased electronegativity).
- Answer
- Each element has an isoelectronic valence shell electron configuration, with the principle quantum number getting larger, meaning the valence electrons are farther away from the nucleus. This means they are less tightly held and so it would be less electronegative.
Without a table of electronegativities, would you be expected to know which would be greater
a). Mercury or Silver?
b). Mercury or Indium?
- Answer
-
a) No, as going up the periodic table increases \(\chi\) while going right to left decreases it. That is, (\(\chi\)-{Cd}>(\(\chi\)-{Hg} while (\(\chi\)-{Ag}<(\(\chi\)-{Cd}, and you do not know which effect is the greater. (The trends oppose each other.)
b) Yes, as going up and left to right both increase \(\chi\), (\(\chi\)-{Cd}>(\(\chi\)-{Hg} but going right to left decreases, (\(\chi\)-{In}>(\(\chi\)-{Cd}, so In must be greater than Hg
Rule of Thumb: Predicting Bond Types
As a "rule of thumb", electronegativity differences can be used to predict if a bond will be covalent, polar covalent or ionic. If the difference in \(\chi\) between two bonding atoms is less than 1/2, they are of very similar electronegativity and it is a covalent bond. If it is greater than 2 they are substantially different and more electronegative atom completely removes a valence electron from the electropositive, forming an ionic compound, and if it is between 0.5 and 2.0 it is polar covalent.
| Difference in Electronegativity (\(\chi\)) | Bond Type | Example |
|---|---|---|
| <0.5 | Covalent or metallic | Cl-Cl (\(\Delta \chi\)=0), C-H (\(\Delta \chi\)=0.35) |
| 0.5-2.0 | Polar Covalent | H-Cl (\(\Delta \chi\)=0.96) |
| >2.0 | Ionic | Na-Cl (\(\Delta \chi\)=2.23) |

Figure \(\PageIndex{4}\): Illustration of different bond types between atoms of different electronegativities (see table 8.7.1 for \(\chi\) values and table 8.7.2 for (\(\Delta \chi\) values).
Van Arkel-Ketelaar (VAK) Diagram
Now that we have covered periodic trends in electronegativity it is a good time to revisit the Van Arkel-Ketelaar (VAK) diagram introduced in the introduction of this Chapter, although this is being done with the caveat that this Chapter focuses on covalent and polar covalent bonds. In the VAK diagram the X axis is the average electronegativity of the two atoms in a bond, which can only be a high value if they are both nonmetals and only be a low value if they are both metals, and so metallic bonds would be on the left and covalent bonds (between two nonmetals) on the right. The Y-axis is the difference in electronegativity, a value that can only be a high value if one is a metal and the other a nonmetal, which also results in an average value that is midway between the metal and a nonmetal, and this results in triangular structure where the top would represent ionic bonds between metals and nonmetals.
The following youtube is an animation that shows the difference between covalent, polar covalent and ionic bonds based on the difference in electronegativity of the bonding atoms.
Animated YouTube going over electronegativity and bond types
Second YouTube going over bonds types and electronegativity.
Dipole Moments of Diatomics
If the difference in electronegativity between the atoms of a bond are between 0.5 and 2.0 we can determine that the bond is polar, and if the atom is a diatomic, that must result in a polar molecule.
\[ \begin{matrix}
_{\delta ^{+}}& & _{\delta ^{-}}\\
H\; \; &-& Cl
\end{matrix} \]
Polar molecules have a positive and negative end, which will align with an external electric field as shown in Figure 8.7.4
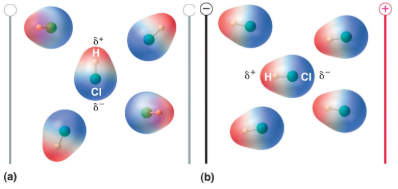
Figure \(\PageIndex{6}\) Shows the effect of an electric field on a polar molecule. In that absence of an external electric field (a) the molecules have random orientation, in the presence of an electric field (b) they align with the field as the \(\delta ^{+}\) end of the polar molecule is attracted towards the negative plate of the external field and the \(\delta ^{-}\) end is attracted towards the positive plate of the external field. Since the molecule is being pulled in opposite directions it does not migrate to the plate the way an ion would, but aligns with the field.
It should be noted that there are attractive interactions between the red \(\delta ^{+}\) end of one molecule with the blue \(\delta ^{-}\), but in the gas phase these interactions are essentially negligible.
Dipole Moment
An electric dipole occurs when two equal charges are separated by a distance. The dipole moment is a vector \(\vec{\mu}\), which is a measure of the electric dipole's strength and orientation and has the units of the Debye. The dipole moment of a molecule is a function of the partial charges of the polar bond, and the distance between them. Ignoring the vector aspects, this can be calculated by Equation:
\[\mu = qr\]
where
- \(\mu\) is the dipole moment (really a vector)
- q is the magnitude of the partial charges \(q^+\) or \(q^-\) (or the more commonly used terms \(δ^+\) and \(δ^-\)), and
- r is the distance between the two charges of the dipole moment (which is also a vector).
The Debye is a very small unit, which in terms of SI base units has a value of 3.34x10-30 Amp meter seconds. Note, Yocto, (10-24) is the smallest SI prefix and this is of the order of 106 times smaller!
Relating Dipole Moments to \(\Delta \chi\) and bond lengths:
In table 8.7.2 we look at the diatomic molecules between H and the halogens. We note that as you go down the periodic table the bond length increases, which would result in a large dipole moment. But it goes down because the \(\Delta \chi\) decreases to a greater extend. So the difference in electronegativity is the major factor in determining the strength of the polarity of a molecule.
| Compound | Bond Length (Å) | Electronegativity Difference | Dipole Moment (D) |
|---|---|---|---|
| HF | 0.92 | 1.9 | 1.82 |
| HCl | 1.27 | 0.9 | 1.08 |
| HBr | 1.41 | 0.7 | 0.82 |
| HI | 1.61 | 0.4 | 0.44 |
Note:
In this class you will not be performing calculations with \(\mu\), but you do need a conceptual understanding, and you need to understand the difference between the charge of an ion, and the magnitude of the dipole moment of a polar molecule. So far we have kept to simple diatomics. In the next section we will move onto compounds with more than one polar bond, and see that the orientation of the bonds affects the polarity of a molecule, and that a symmetric molecule like carbon dioxide has polar bonds, but is in itself, nonpolar.
Contributors
Contributors and Attributions
Robert E. Belford (University of Arkansas Little Rock; Department of Chemistry). The breadth, depth and veracity of this work is the responsibility of Robert E. Belford, rebelford@ualr.edu. You should contact him if you have any concerns. This material has both original contributions, and content built upon prior contributions of the LibreTexts Community and other resources, including but not limited to:
- Anonymous


