2.6: Ionic Compounds and Formulas
- Page ID
- 50431
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
Learning objectives
- Relate the stability of ionic compounds to Coulomb’s Law
- Recognize properties of ionic compounds
- Recognize that metals lose electrons to form cations and that nonmetals gain electrons to form anions
- Predict the charge of monatomic main group elements based on their group number.
- Name monoatomic anions and cations
- Memorize polyatomic ions
- Write formulas for ionic compounds using monatomic and polyatomic ions by applying the principle of charge neutrality.
Introduction
In the preceding section we discussed covalent bonds of molecules and introduced the concept of ionic bonds. In this section we will develop a deeper understanding of ionic compounds. We will see that to be stable an ionic compound must be neutral, and that there is not a discrete formula as there is with covalent compounds, in fact we use the lowest ratio of positive to negative charged ions that results in a neutral formula. In the previous section we did introduce the concept of cations (positive ions) and anions (negative ions). In the next section we will go over nomenclature, the naming of compounds.
Coulomb's Law
Coulomb's Law is a mathematical formula that describes the electrostatic interaction between two charged particles that was first proposed by the French physicist Charles Coulomb (1736–1806). Coulomb's law is often called an inverse square law, as the force decreases as a function of the square of the distance between the two particles.
\[ E= k\dfrac{q_1q_2}{ r} \; \; \; \; \; \; \; \; F= k\dfrac{q_1q_2}{r^2}\]
- \(E\) is the potential energy
- \(F\) is the force
- \(r\) is the distance of separation (note that the potential goes to zero when they are separated by infinity)
- \(q\) is the charge of the ions
- \(k\) is a constant

The electrostatic interactions can be understood by the above image, where in (a), like charges repel and in (b), opposite charges attract. If you look at Coulomb's law, you note that in (a) the force is positive (because both q1 and q2 are negative), while in (b) the force is negative (because q1 is negative while q2 is positive). That is, attractive interactions result in a lowering of the energy
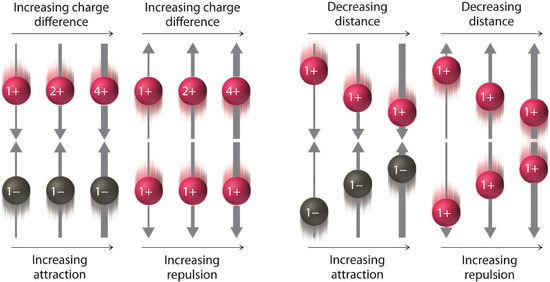
In the above diagram the width of the arrows indicate the magnitude of the forces of electrostatic interaction. You should be able to look at the algebra associated with Coulomb's Law and see how it results in these interactions. In the numerator is the charge, and so the greater the charge, the greater the interaction. In the denominator is the distance between the charges, and so the larger the distance, the weaker the interaction.
NOTE: It is very important that you learn how to "read" algebraic equations like Coulomb's Law. Math is actually a universal language and being able to read equations is one of the most important skills you can learn in this class. That is, it makes no difference what language you study in, the math is still the same, and being able to read equations is a fundamental skill you should gain from this class.
Exercise \(\PageIndex{1}\)
Using the principle of Coulombs Law, would you expect \(KCl\) or \(\ce{Al2O3}\) to have a greater melting point, noting that the stronger the forces of attraction the higher the temperature required to melt the compound?
- Answer
-
According to Coulombs Law, the greater the charge, the stronger the interaction between ions and the greater energy (temperature) needed to separate the ions, so Aluminum oxide would be predicted to have a higher melting point than potassium chloride.
Crystal Lattice and Principle of Charge Neutrality
Why must ionic compounds be neutral?
An ionic bond is not between two ions, but the result of the interaction of multiple cations ([+] ions) and anions ([-] ions) as the coordinate with each other and form an ionic crysta. Salts are typical ionic compounds. That is, a salt crystal has +/+ and -/- repulsions (increasing the energy), and +/- attractions (decreasing the energy, and making the compound more stable), and if the attractive forces are greater than the repulsive, an ionic compound is formed. In the following diagram we see how a crystal forms which maximizes the attractive interactions of the opposite charges while minimizing the repulsive interactions of the like charges. If the compound was not neutral, but had more cations, or more anions, the like/like repulsive forces would be larger and the material would become unstable and break apart. Therefore, ionic compounds must be neutral.
 |
Figure \(\PageIndex{3}\): In the above image the sodium (a metal) loses and electron (becoming smaller) while the Chlorine atom (nonmetal) gains an electron (becoming bigger). A crystal lattice results where the cations and anions pack in three dimensional space that can result in a macroscopic crystal that is visible to the naked eye (CC BY-SA-NC; anonymous).
The salt crystals seen to the naked eye are the result of the way cations and anions pack to form a stable crystal structure that minimizes like/like repulsions and maximizes opposite charge attractions as defined by Coulomb's Law. The following video from YouTube describes the formation of sodium chloride.
Properties of Ionic Compounds
Because of the arrangement of cations and anions in a the crystal lattice, these ions are held tightly into their position. Although the ions can vibrate and oscillate about their position, it take much more energy than room temperature for one ion to break free of the lattice structure. This results in very high melting points and boiling points for ionic compounds. Therefore, ionic compounds are crystal solids at room temperature. They are not malleable or soft. When struck sharply, they do shatter cleanly, with layers of ions breaking off at once.
Monatomic Ions
Metals tend to form cations and nonmetals tend to form anions. The following periodic table shows some of the common ions formed by common elements. Note, the noble gasses (turquoise) do not tend to form ions.
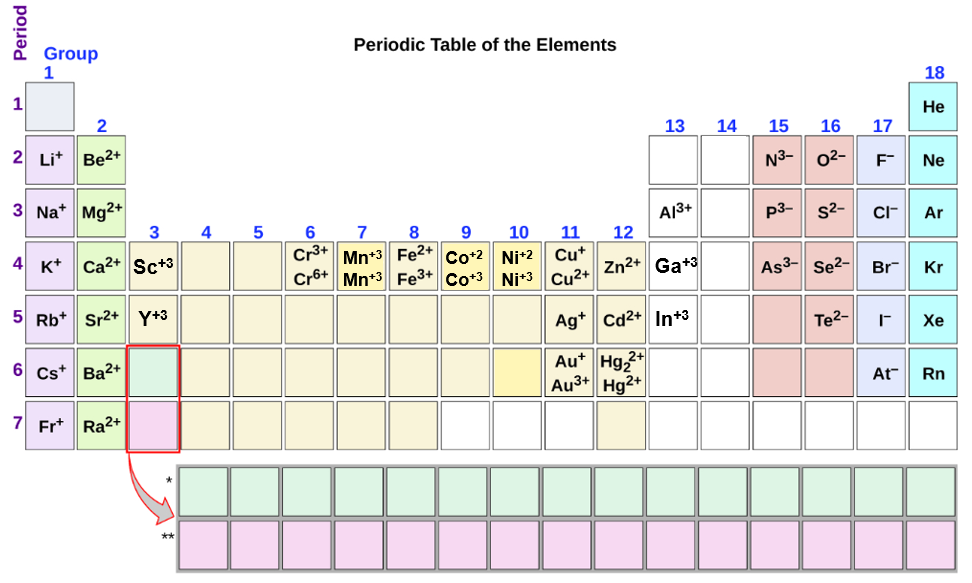
Figure \(\PageIndex{4}\) should not be considered to be a comprehensive Figure and this topic will be brought up again in the next section. There are several things you can note from this table though. First, metals tend to from cations and nonmetals tend to form anions, while the noble gasses do not tend to form ions. Second, the nonmetals have only one charge state, which represents the number of electrons that need to be added for them to have the same number as a noble gas. Third, there are two types of metals, those that have only one charge state (like the nonmetals), and those that have multiple charge states. These different types of ion forming metals will be discussed more in the next section on naming compounds (section 2.7.3).
Monatomic Cations:
When atoms (typically metals) lose one or more electrons the become positively charged cations. For example, when a neutral sodium atom loses one electron, it becomes the sodium ion, Na+ as shown in the following shorthand notation:
\[\ce{Na -> Na^{+} + e^{-}}\]
Another example shows the formation of the magnesium ion from the neutral magnesium atom losing 2 electrons to pick up a +2 charge.
\[\ce{Mg -> Mg^{2+} + 2e^{-}}\]
Can we predict the stable charge of a monoatomic cation?
Yes, it is easy for non-transition metals that have only one charged state (alkali metals, alkaline earth and post-transition metals - see Figure 2.4.2). The trick is to remove enough electrons so that the cation has the same number of outer shell electrons as a noble gas, that is, it is isoelectronic to the noble gas. This is easy if we use the atom's group number's in terms of the "A" designation (remember there are two conventions for numbering the groups), as the group number effectively tells you how many electrons are needed to be removed. So Sodium (Group 1A) has 11 electrons and so if it looses one it has 10, like Neon (a noble gas). Magnesium has 12, so it looses 2 to become like Neon, and Aluminum has 13 and so looses 3 to become like Neon.
Note: Why does hydrogen not form a +1 cation?
Although hydrogen has one electron in its outer shell (like all the alkali metals), it only has one electron and so completely removing it would leave behind a bare nucleus, a subatomic particle the proton, which would not be stable. Consequently hydrogen does not form a cation, but can result in an acid, which is a polar covalent bond. In the above video sodium with 11 electrons gave an electron to chlorine, forming the \(\ce{Na^{+}}\) cation and the \(\ce{Cl^{-}}\) anion, which then formed the crystal table salt NaCl. If chlorine was to try and remove the electron from hydrogen, it would not be able to as the resulting nucleus would pull it back, this results in the molecular acid HCl, where the chlorine can not completely remove the electron from the hydrogen. This is called a "polar covalent bond" and will be discussed later this semester.
Monatomic Anions:
When atoms (typically non-metals) gain one or more electrons they become negatively charged anions. For example, when a neutral fluorine atom gains one electrons, it becomes the fluoride ion as shown by the following shorthand notation:
\[\ce{F + e^{-} → F^{-}}\]
Another example is the formation of the sulfide ion when a neutral sulfur atom gains two electrons picking up a -2 charge.
\[\ce{S + 2e^{-} → S^{2-}}\]
Can we predict the stable charge of a monoatomic anion?
Yes, just as with the monatomic cations, stable monatomic anions are isoelectronic to the nearest noble gas, but in this case you add electrons instead of subtract. Once again, if we use the "A" designations for numbering the groups, we simply add the number of electrons required to be the same as a noble gas. So chlorine gains 1, oxygen gains 2 and nitrogen gains 3. This number can be determined by taking the group number 5, 6 or 7 from groups 5A, 6A and 7A and subtracting from 8 (for group 8A).
Exercise \(\PageIndex{2}\)
Based on the position of the periodic table, predict the charge of the following elements if they are to produce ions. (do not look at periodic table above to come up with your answer)
- Sr
- Ga
- P
- Answer
-
A) \(\ce{Sr^{2+}}\). Sr is a group 2A main group metal. So, +2 charge.
B) \(\ce{Ga^{3+}}\). Ga is a group 3A main group metal. So, +3 charge.
C) \(\ce{P^{3-}}\). P is a group 5A main group nonmetal. So, 5-8 = -3 charge.
Polyatomic Ions
Many ions contain more than one nuclei and these are labeled at polyatomic Ions. There are different types of polyatomic ions. We will look at two common types, oxyanions and carboxyanions. Students need to memorize the polyatomic ions in Figure \(\PageIndex{5}\) by the time the get to then next section as they will be using this in naming ionic compounds.
When forming a stable crystal, these compounds have both covalent bonds (holding the polyatomic ions together), and ionic bonds (holding the cations and anions together in a stable neutral lattice).
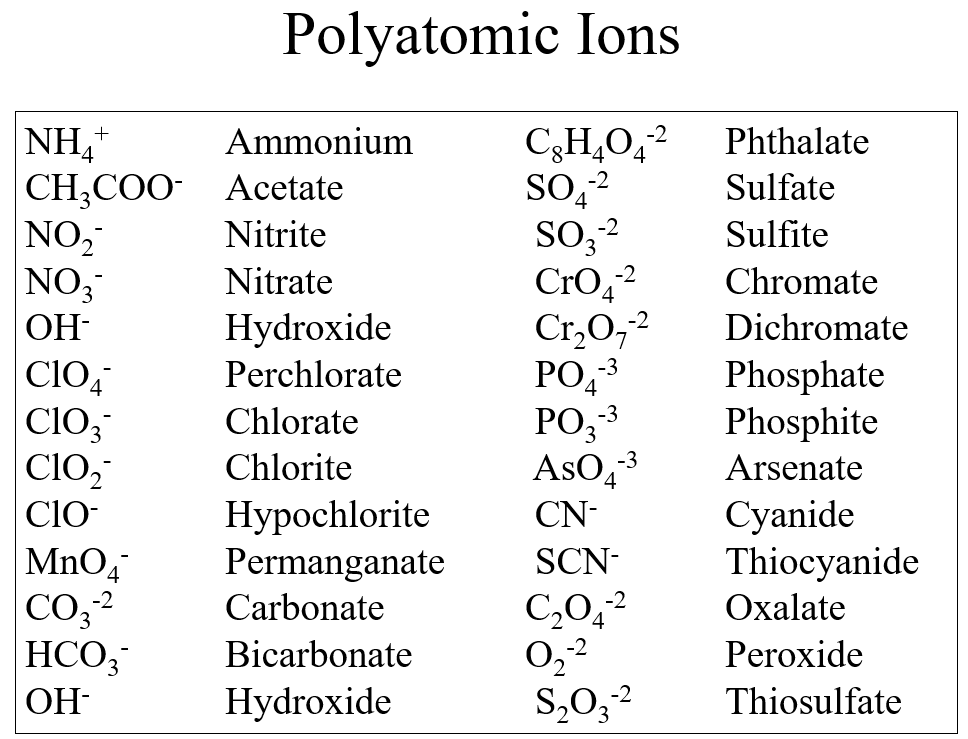
What you may notice is there are several types of structural features to these ions, and we will look at two, the oxyanions and the carboxyanions.
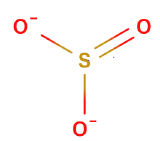
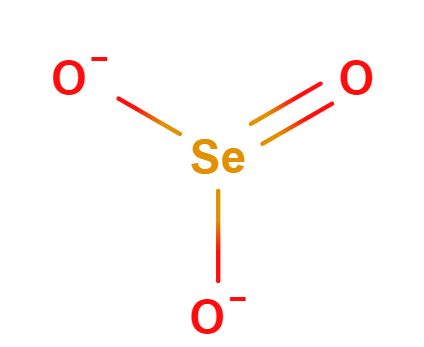
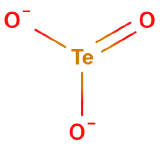
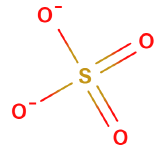
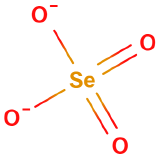
Oxyanions
Oxyanions have a central nonmetal with oxygens covalently bonded to them. The atoms of the same periodic family tend to from analogous oxyanions
 |
 |
 |
 |
 |
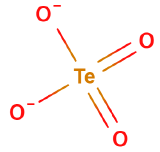 |
| sulfite | selenite | tellurite | sulfate | selenate | tellurate |
Figure \(\PageIndex{6}\): Polyatomic ions of group VIA, -ites on the left, -ates on the right.
The larger halogens (chlorine, bromine and iodine) form four types of oxyanions, as exemplified by chlorine here.
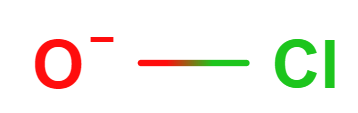 |
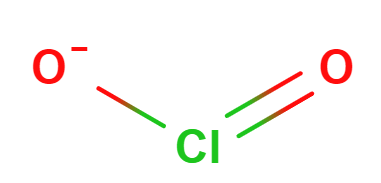 |
 |
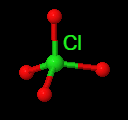 |
| hypochlorite | chlorite | chlorate | perchlorate |
Figure \(\PageIndex{7}\): The four oxyanions of chlorine. Note that in all cases, the oxygens have covalent bonds to the chlorine, which is the central nonmetal ion. The other halogens form similar types of oxyanions.
Carboxylate ions
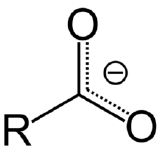
Carboxylate is a functional group that gives can hold a negative charge in an organic compound. The left most box of Figure \(\PageIndex{8}\) shows the generic structure of a carboxylate ion, where R represents some organic compound, and the carboxylate is also attached to two oxygens which"share" the electron. There are three carboxylate ions students are required to memorize and their structures are represented in Figure \(\PageIndex{8}\):
 |
 |
 |
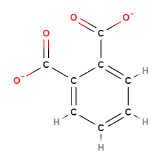 |
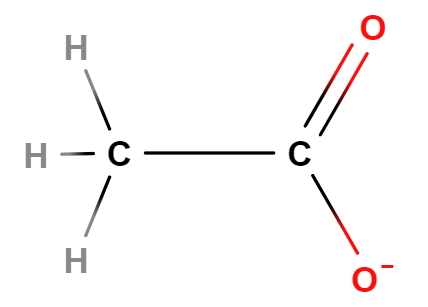
| generic carboxylate ion | Acetate | Oxalate | Phthalate |
| Formula | CH3(CO2-) | (CO2-)2 | C6H4(CO2-)2 |
| Description | Attached to carbon | two attached to each other | attached to benzene ring |
Figure \(\PageIndex{8}\): Recognizing that these ions have carboxylate groups makes it easier to remember their formula, as they are all similar in structure
Right now the important thing is to understand what a polyatomic ion is. In the next section on nomenclature we will build up on this structural information to come up with some tricks to make memorizing names easier.
Ionic Compound Formula and the Principle of Charge Neutrality
The Principle of Charge Neutrality simply states that for matter to be stable it must be neutral. If an ionic compound had a formula of Na2F, and you had 10,000 of those units, then there would be 20,000 positive things and 10,000 negative things, meaning an excess of 10,000 positive things repelling each other, and so it would not be stable, and so would not form (and realize that real substances on macrosocopic scales that we can measure have in the order of 1023 entities.
You might ask, if something is neutral, why are the ion-ion attractions greater than the repulsion, that is, why isn't the energy of interaction neutral? The reason that the attractions are greater than the repulsions is because opposite ions tend to be closer together (they are attracted) than the ions of same sign (they are repulsed), and according to Coulomb's law, the closer they are the greater the force, and so a neutral compound has a net attractive force and forms a stable compound.
The formula of an ionic compound represents the lowest whole number ratio of cations to anions, it is as simple as that. Most cations have charges of [+1] through [+6] while most ions have charges of [-1] through [-3].
Trick:
Set # of Anions = Charge of Cation and
set # of Cations = Charge of Anion
Beware that this must be the Lowest Whole # Ratio of cation to anion.
Strategy:
- Identify charge of each ion
- multiply charge of each ion by absolute value of the charge of the counter ion.
- Make sure resulting ratio is the lowest whole number ratio, if not, divide by common denominator so all values are integers.
Watch video \(\PageIndex{2}\) to see how to perform this calculation
Exercise \(\PageIndex{3}\)
What is the formula for the ionic compound that forms when the calcium ion reacts with the oxide ion?
- Answer
-
\(CaO\). \(Ca^{2+}\) and \(O^{2-}\). You need one calcium ion for every one oxide ion for the compound to be charge neutral.
s
Exercise \(\PageIndex{4}\)
What is the formula for the ionic that forms when the lead(IV) (\(\ce{Pb^{4+}}\)) ion reacts with the sulfate (\(\ce{SO4^{2-}}\)) ion?
- Answer
-
Add \(\ce{Pb(SO4)2}\). \(\ce{Pb^{4+}}\) and \(\ce{SO4^{2-}}\). For every one Lead(IV) ion, you need two sulfate ions to be charge neutral. 1(+4) + 2(-2)=0. You may use the criss-cross rule, but you must make sure that you reduce to the simplest whole number ratio.
Determining Ion Charges from Formula
If given a formula like NaCl or FeO or Fe2O3 you need to be able to calculate the charge of the ions. In the case of NaCl it is easy as Na is always [+1] and Cl is always [-1]. But iron can have multiple charges and so needs to be Figured out.
Fortunately, the anion is always of known charge and so you can use that to algebraically reverse engineer the principle of charge neutrality. that is for a general formula CxAy where C is the Cation with charge [+m] and there are x of them, and A is the Anion with charge of [-n] and there are y of them, we know from the principle of charge neutrality that
\[x(+m) +y(-n) =0 \\ \therefore \\ x=\frac{0-y(-n)}{x}\]
So for FeO we know the charge of the oxygen is -2, so 1(charge of Fe) +1(charge of O) = 0, so Fe=+2 as )=-1
for Fe2O3 we have
2(charge of Fe) + 3(charge of Oxygen) = 0
so \[2(+m) +3(-2) =0 \\ \therefore \\ +m=\frac{0-3(-2)}{2} = 3\]
that is: 3x2 -2x3=0, which makes sense.
Exercise \(\PageIndex{5}\)
What is the the charge for the cation in each of the following comounds?
a. \(V_2O_5\)
b. \(Pb_3N_4\)
- Answer
-
a. \(V^5\) because oxygen is minus 2.
b. \(Pb^4\) because nitrogen is minus 3.
Test Yourself
Query \(\PageIndex{1}\)
Contributors
Robert E. Belford (University of Arkansas Little Rock; Department of Chemistry). The breadth, depth and veracity of this work is the responsibility of Robert E. Belford, rebelford@ualr.edu. You should contact him if you have any concerns. This material has both original contributions, and content built upon prior contributions of the LibreTexts Community and other resources, including but not limited to:
- Elena Lisitsyna (H5P interactive modules)


