10.7: Nonideal Gases
- Page ID
- 52153
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Skills to Develop
- To recognize the differences between the behavior of an ideal gas and a real gas.
- To understand how molecular volumes and intermolecular attractions cause the properties of real gases to deviate from those predicted by the ideal gas law.
The postulates of the kinetic molecular theory of gases ignore both the volume occupied by the molecules of a gas and all interactions between molecules, whether attractive or repulsive. In reality, however, all gases do have volume and occupy space. Furthermore, the molecules of real gases interact with one another in ways that depend on the structure of the molecules and therefore differ for each gaseous substance. In this section, we consider the properties of real gases and how and why they differ from the predictions of the ideal gas law. We also examine liquefaction, a key property of real gases that is not predicted by the kinetic molecular theory of gases.
Pressure, Volume, and Temperature Relationships in Real Gases
For an ideal gas, a plot of \(PV/nRT\) versus \(P\) gives a horizontal line with an intercept of 1 on the \(PV/nRT\) axis. Real gases, however, show significant deviations from the behavior expected for an ideal gas, particularly at high pressure, where particles are forced close to each other and so the gas deviates from the Kinetic Molecular Theory's postulate stating that the volume of the gas particle is negligible. Only at relatively low pressures (less than 1 atm) do real gases approximate ideal gas behavior (part (b) in Figure \(\PageIndex{1}\)).
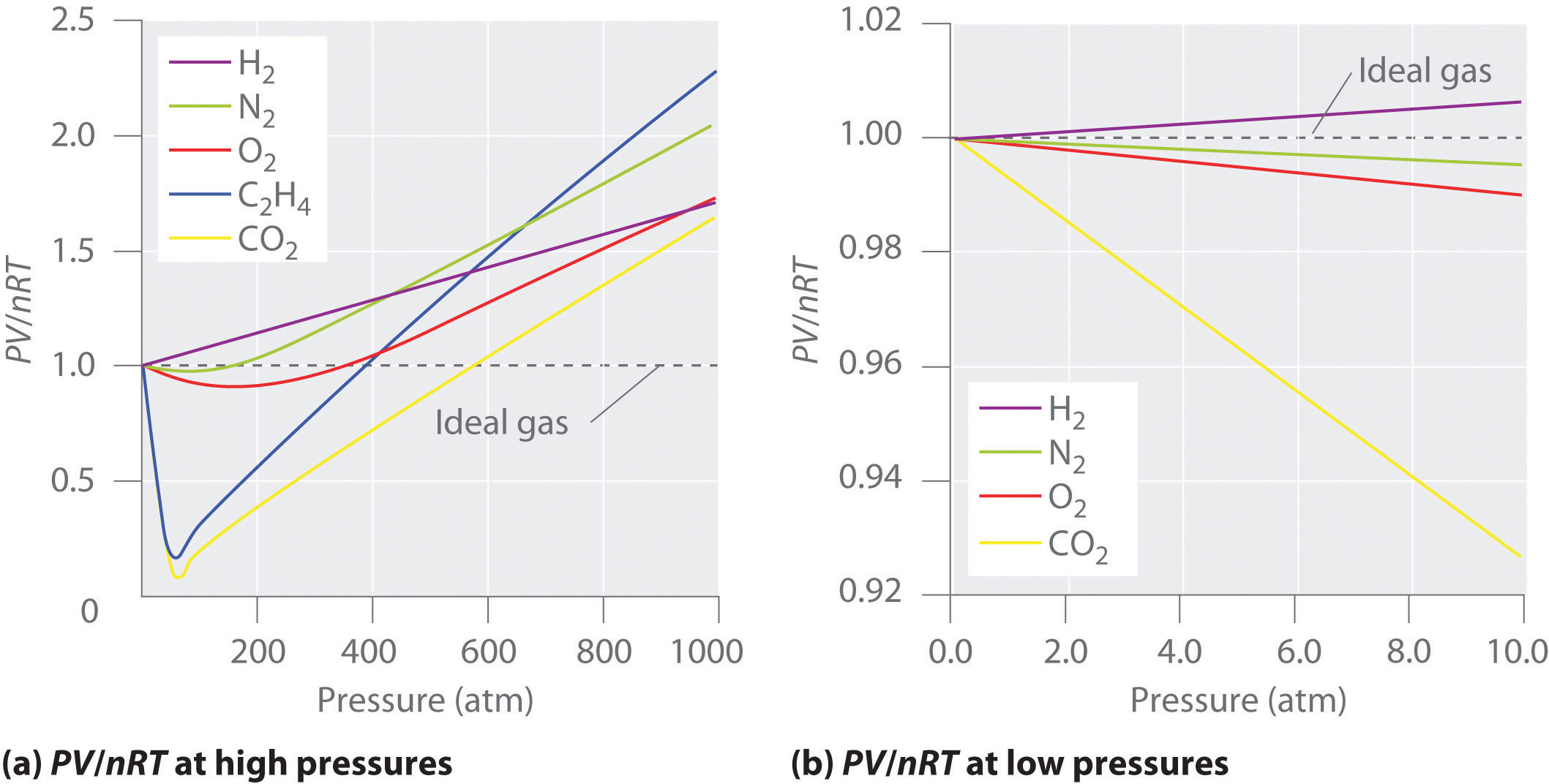
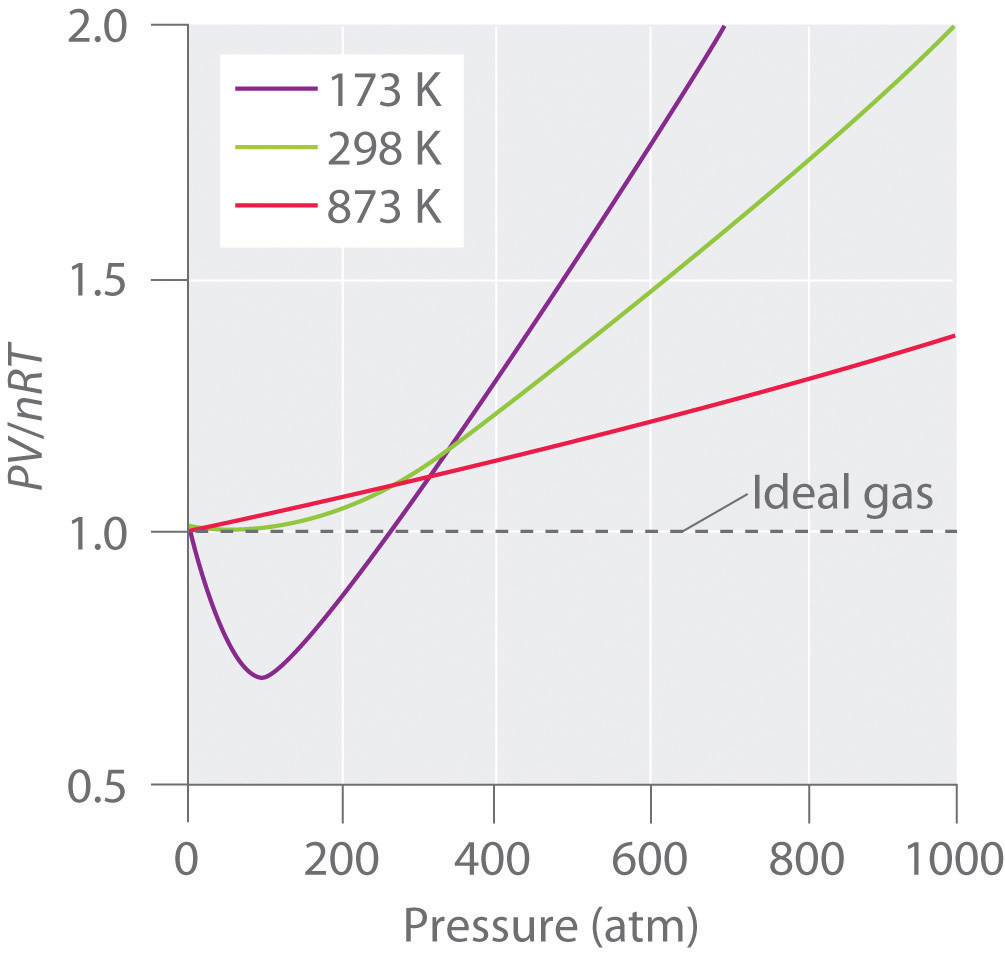
Real gases also approach ideal gas behavior more closely at higher temperatures, as shown in Figure \(\PageIndex{2}\) for \(N_2\). Why do real gases behave so differently from ideal gases at high pressures and low temperatures? Under these conditions, the two basic assumptions behind the ideal gas law—namely, that gas molecules have negligible volume and that intermolecular interactions are negligible—are no longer valid.
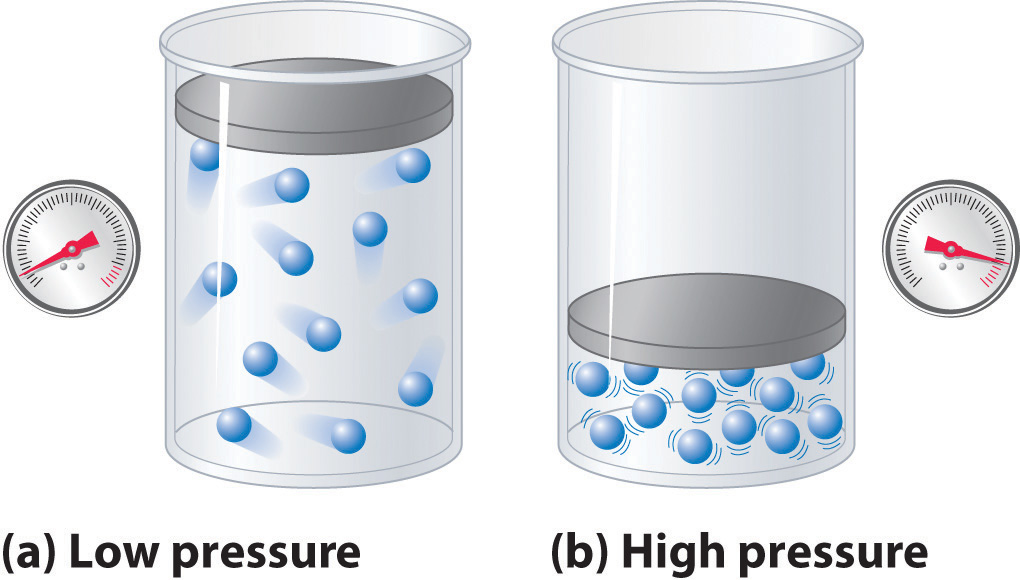
Because the molecules of an ideal gas are assumed to have zero volume, the volume available to them for motion is always the same as the volume of the container. In contrast, the molecules of a real gas have small but measurable volumes. At low pressures, the gaseous molecules are relatively far apart, but as the pressure of the gas increases, the intermolecular distances become smaller and smaller (Figure \(\PageIndex{3}\)). As a result, the volume occupied by the molecules becomes significant compared with the volume of the container. Consequently, the total volume occupied by the gas is greater than the volume predicted by the ideal gas law. Thus at very high pressures, the experimentally measured value of PV/nRT is greater than the value predicted by the ideal gas law.
Moreover, all molecules are attracted to one another by a combination of forces. These forces become particularly important for gases at low temperatures and high pressures, where intermolecular distances are shorter. Attractions between molecules reduce the number of collisions with the container wall, an effect that becomes more pronounced as the number of attractive interactions increases. Because the average distance between molecules decreases, the pressure exerted by the gas on the container wall decreases, and the observed pressure is less than expected. Thus as shown in Figure \(\PageIndex{2}\) , at low temperatures, the ratio of \(PV/nRT\) is lower than predicted for an ideal gas, an effect that becomes particularly evident for complex gases and for simple gases at low temperatures. At very high pressures, the effect of nonzero molecular volume predominates. The competition between these effects is responsible for the minimum observed in the \(PV/nRT\) versus \(P\) plot for many gases.
Note
Nonzero molecular volume makes the actual volume greater than predicted at high pressures; intermolecular attractions make the pressure less than predicted.
At high temperatures, the molecules have sufficient kinetic energy to overcome intermolecular attractive forces, and the effects of nonzero molecular volume predominate. Conversely, as the temperature is lowered, the kinetic energy of the gas molecules decreases. Eventually, a point is reached where the molecules can no longer overcome the intermolecular attractive forces, and the gas liquefies (condenses to a liquid).
The van der Waals Equation
The Dutch physicist Johannes van der Waals (1837–1923; Nobel Prize in Physics, 1910) modified the ideal gas law to describe the behavior of real gases by explicitly including the effects of molecular size and intermolecular forces. In his description of gas behavior, the so-called van der Waals equation,
\[ \left(P + \dfrac{an^2}{V^2}\right) (V − nb)=nRT \]
a and b are empirical constants that are different for each gas. The values of \(a\) and \(b\) are listed in Table \(\PageIndex{1}\) for several common gases.

| Gas | a ( (L2·atm)/mol2) | b (L/mol) |
|---|---|---|
| He | 0.03410 | 0.0238 |
| Ne | 0.205 | 0.0167 |
| Ar | 1.337 | 0.032 |
| H2 | 0.2420 | 0.0265 |
| N2 | 1.352 | 0.0387 |
| O2 | 1.364 | 0.0319 |
| Cl2 | 6.260 | 0.0542 |
| NH3 | 4.170 | 0.0371 |
| CH4 | 2.273 | 0.0430 |
| CO2 | 3.610 | 0.0429 |
The pressure term in the van der Waals equation (\(P + (an^2/V^2)\)) corrects for intermolecular attractive forces that tend to reduce the pressure from that predicted by the ideal gas law. Here, \(n^2/V^2\) represents the concentration of the gas (\(n/V\)) squared because it takes two particles to engage in the pairwise intermolecular interactions of the type shown in Figure \(PageIndex{4}\). The volume term \(V − nb\) corrects for the volume occupied by the gaseous molecules.

The correction for volume is negative, but the correction for pressure is positive to reflect the effect of each factor on V and P, respectively. Because nonzero molecular volumes produce a measured volume that is larger than that predicted by the ideal gas law, we must subtract the molecular volumes to obtain the actual volume available. Conversely, attractive intermolecular forces produce a pressure that is less than that expected based on the ideal gas law, so the an2/V2 term must be added to the measured pressure to correct for these effects.
Example \(\PageIndex{1}\):
You are in charge of the manufacture of cylinders of compressed gas at a small company. Your company president would like to offer a 4.00 L cylinder containing 500 g of chlorine in the new catalog. The cylinders you have on hand have a rupture pressure of 40 atm. Use both the ideal gas law and the van der Waals equation to calculate the pressure in a cylinder at 25°C. Is this cylinder likely to be safe against sudden rupture (which would be disastrous and certainly result in lawsuits because chlorine gas is highly toxic)?
Given: volume of cylinder, mass of compound, pressure, and temperature
Asked for: safety
Strategy:
A Use the molar mass of chlorine to calculate the amount of chlorine in the cylinder. Then calculate the pressure of the gas using the ideal gas law.
B Obtain a and b values for Cl2 from Table 6.9.1. Use the van der Waals equation to solve for the pressure of the gas. Based on the value obtained, predict whether the cylinder is likely to be safe against sudden rupture.
Solution:
A We begin by calculating the amount of chlorine in the cylinder using the molar mass of chlorine (70.906 g/mol):
\[n=\dfrac{m}{M}=\rm\dfrac{500\;g}{70.906\;g/mol}=7.052\;mol\]
Using the ideal gas law and the temperature in kelvins (298 K), we calculate the pressure:
\[P=\dfrac{nRT}{V}=\rm\dfrac{7.052\;mol\times0.08206\dfrac{L\cdot atm}{mol\cdot K}\times298\;K}{4.00\;L}=43.1\;atm\]
If chlorine behaves like an ideal gas, you have a real problem!
B Now let’s use the van der Waals equation with the a and b values for Cl2 from Table 6.9.1. Solving for P gives
\[\begin{split}P&=\dfrac{nRT}{V-nb}-\dfrac{an^2}{V^2}\\&=\rm\dfrac{7.052\;mol\times0.08206\dfrac{L\cdot atm}{mol\cdot K}\times298\;K}{4.00\;L-7.052\;mol\times0.0542\dfrac{L}{mol}}-\dfrac{6.260\dfrac{L^2atm}{mol^2}\times(7.052\;mol)^2}{(4.00\;L)^2}\\&=\rm28.2\;atm\end{split}\]
NothingThis pressure is well within the safety limits of the cylinder. The ideal gas law predicts a pressure 15 atm higher than that of the van der Waals equation.
Exercise \(\PageIndex{1}\)
A 10.0 L cylinder contains 500 g of methane. Calculate its pressure to two significant Figures at 27°C using the
- ideal gas law.
- van der Waals equation.
- Answer a
-
77 atm
- Answer b
-
67 atm


