3: Absorbance Spectroscopy
- Page ID
- 361518
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Absorbance Spectroscopy
A spectrophotometer in an instrument that measures the amount of light absorbed at a specific wavelength (\(\lambda\)) by a sample, and can be used to generate a spectrum, which is a plot of the absorbance as a function of the wavelength. In gen chem 1 we studied atomic line spectra, (section 6.3), where each atom had a unique spectrum that could be used to identify element the atom was. We developed the Bohr model for the hydrogen atom (section 6.3.3) that quantized the electronic energy levels, and could describe the spectrum of hydrogen in terms of electrons absorbing the energy of the photon (Ephoton= h\(\nu\)=hc/\(\lambda\)) as the electron transitioned from lower energy orbital to higher energy one. The same principle works here, except that when ultraviolet or visible light is absorbed electrons are transitioning between molecular orbitals instead of atomic orbitals, and if the energy gaps between the molecules are different, they will have different spectra.
Remember the color of light is related to its energy and wavelength (E= h\(\nu\)=hc/\(\lambda\)). So the color of a molecule depends on its spectrum. Figure 4.1 is a spectrum of the molecule chlorophyll in the solvent ethanol. Note it absorbs light in the blue (400-450 nm) and red (650-700 nm) regions and so it is green. That is, the color we see is not the color absorbed, but the color transmitted (Figure \(\PageIndex{1}\)). If all wavelengths are absorbed it is black, and if none are it is white.
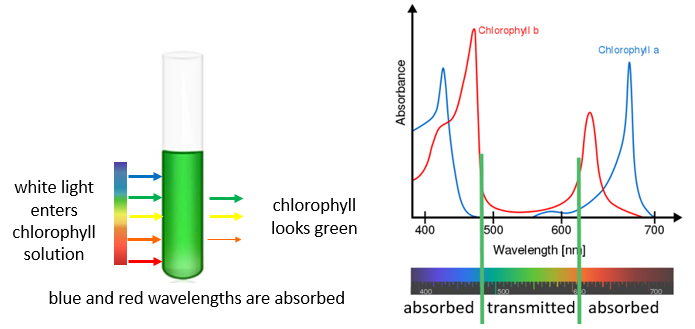 Figure \(\PageIndex{1}\): (a) red and blue light are absorbed by chlorophyll and so it appears its complementary color, green. (Copyright. (a) Belford CC-BY,)
Figure \(\PageIndex{1}\): (a) red and blue light are absorbed by chlorophyll and so it appears its complementary color, green. (Copyright. (a) Belford CC-BY,)
Spectrometer design
The fundamental theory behind the operation of a spectrometer is rather easy to understand and section 10.2 of David Harvey's analytical chemistry LibreText has a good review. The spectrometer and can be considered to consist of 4 major components;
- light source
- monochromator (diffraction grating which creates light of a single wavelength)
- sample cavity (cuvette holder)
- detector.
The particular spectrometer we are using is a CCD (Charge Coupled Device) similar to digital cameras. The light follows an optical path where white light (of all colors) enters the sample and the amount absorbed depends on the color. Then it goes to a Diffraction Grating which splits the colors and they fall on an array of photo detectors which result in a charge displacement proportional to the number of photons which hit that array. You first "calibrate" (zero out) the spectrometer by running a sample of pure solvent (the blank). Then you run your sample. If your sample absorbs some of the light at a wavelength, the number of photons hitting the detector is reduced, that is, the intensity of the light goes down.
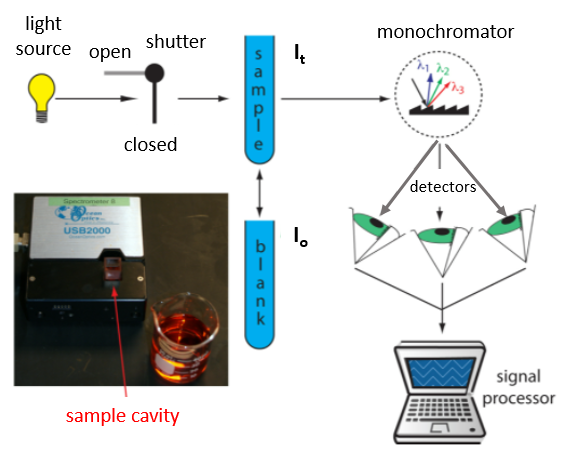 Figure \(\PageIndex{3}\): Schema for USB spectrometer. (Copyright; David Harvey via source)
Figure \(\PageIndex{3}\): Schema for USB spectrometer. (Copyright; David Harvey via source)Absorbance
We do not directly measure absorbance, instead we measure the reduction in the intensity of light as it passes through a sample, which is held in a special transparent container of known path length called the cuvette (figure \(\PageIndex{3}\)).The intensity of light is the number of moles of photons (n) times the energy of each photon (I=nh\(\nu\)), where h is Planck's constant (section 6.2). The light entering the cuvette (figure \(\PageIndex{3}\)) has an intensity of Io and the light transmitted has an intensity It. The transmitted intensity can be measured with a variety of photodetectors that use the principles of Einstein's photoelectric effect (section 6.2.3).
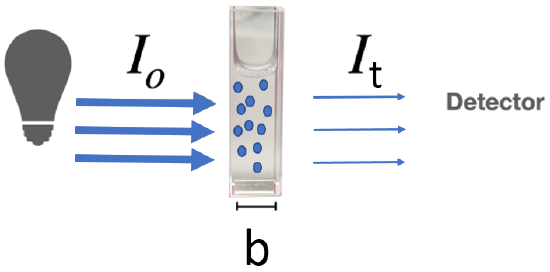 Figure \(\PageIndex{4}\): Light of intensity I0 enters cuvette of path length b that is of a frequency that is absorbed by the blue molecules and so the light transmitted (It) has a reduced intensity. (CC-BY; Kathryn Haas, modified by Belford)
Figure \(\PageIndex{4}\): Light of intensity I0 enters cuvette of path length b that is of a frequency that is absorbed by the blue molecules and so the light transmitted (It) has a reduced intensity. (CC-BY; Kathryn Haas, modified by Belford)What we are measuring is the intensity of light, and we can calculate the Transmittance as the ratio of the light intensity entering the sample to that exiting and percent transmittance to be 100 times that value.
\[\begin{align}T=\frac{I_t}{I_o} && and && \% T=\frac{I_t}{I_o}100 \end{align}\]
If no light is absorbed It=Io and 100% of the light is transmitted, if all the light is absorbed It=0 and no light is transmitted.
As light is absorbed the light intensity entering is always greater or equal to the intensity transmitted \(I_o \geq I_t\).
The absorbance (A) is defined as the log of the ratio of the light intensity entering to that exiting.
\[A=log \frac{I_o}{I_t} \;\;=\;\; log \frac{1}{T}\]
and
\[T=10^{-A} \;\; = \;\; \frac{1}{10^A}\]
So the absorbance is logarithmically related to the reciprocal of the transmittance.
When you run a spectrometer you first run a "blank" of pure solvent and calibrate the instrument by setting that reading to zero, and then you add a sample with your analyte dissolved in the solvent, and if the solute absorbs light at a frequency the absorbance goes up and the percent transmittance goes down. For any spectrometer there is a an upper and lower limit of detection that can be understood by looking at the values in table \(\PageIndex{1}\). As you lower the absorbance the percent transmittance approaches 100% (that of pure solvent) and your detector can not see a difference, while at high absorbance so little light is transmitted that the detector can not detect a signal. For the spectrometers we use in this class we will only trust absorbance values betwee 0.05 and 1.
| Absorbance | % Transmittance | Absorbance | % Transmittance |
|---|---|---|---|
| 0 | 100% | 1 | 10% |
| 0.001 | 99.8% | 2 | 1% |
| 0.01 | 97.7% | 3 | 0.1% |
| 0.05 | 89.1% | 4 | 0.01% |
| 0.1 | 79.4 | 10 | 0.00000001% |
Note
For the spectrometer used in this class we will only trust absorbance values between 0.05 and 1
Beer's Law
There are three factors that influence the number of photons absorbed as light travels through a sample (figure \(\PageIndex{2}\)).
- Path length (the longer the path length the greater the number photons absorbed).
- Concentration of absorbing molecules (typically solute molecules, the more concentrated the more photons absorbed)
- Intensity of the light itself (more photons are absorbed if you shine a bright light on a sample than a dim light).
The rate of change in intensity of light that is proportional to the intensity itself (\(\frac{\Delta I}{\Delta x}=-kI\)), to the concentration of the absorbing molecules and the distance traveled (path length \(\Delta x = b\)). As in the kinetics chapter, this requires calculus to solve and results in a logarithmic relationship that for historical reasons is written in log base 10. The general relationship is
\[\Delta I =-kcI\Delta x\] where k is a proportionality constant, \(\Delta\)x is the change in path length, c is the concentration and I is the light intensity.
Integrating this from the calculus (see "Deeper Dive") gives us the relationship
\[log \frac{I_0}{I_t}=\epsilon bc\]
From above absorbance (A) is defined as
\[A=log \frac{I_0}{I_t}\]
and this results in Beer's Law, which is the relationship you need to use in this lab.
Beer's Law
\[A=\epsilon bc\]
where,
A=absorbance
\(\epsilon\) = the extinction coefficient or the molar absorptivity constant with typical units of M-1cm-1.
b = path length
c = concentration of absorbing molecules
Students need to know Beer's Law but are not required to derive it. You will use a spectrometer that will read the absorbance for solutions of various concentrations.
Deeper Dive \(\PageIndex{1}\)
Note, Beer's law comes from the calculus as the absorbance (A) is related to the log of the intensity change as light travels through a sample. There will be many equations we cover in this class that are derived from the calculus, which is not a prerequisite for this class. Many students have taken calculus and others might like to know where this relationship comes from and so it is embedded in the link below. You will not be tested on the derivation of the Beer's law, but you will be required to know Beer's Law and the definition of absorbance, and use algebra to caculate values based on these equations.
- Calculus derivation of Beer's Law
-
\[dI = -kcIdx \\ \; \\ \frac{dI}{I}=-kcdx \\ \; \\ \int_{I_o}^{I_t}\frac{dI}{I}=-\int_{0}^{b}kcdx
\\ \; \\ lnI_t-ln_o = ln(\frac{I_t}{I_0})=-kcb \\ \; \\ ln(\frac{I_o}{I_t})=kcb\]So after converting to log base 10 (which is done for historical reasons) we get
\[A=log \frac{I_0}{I_t}=\epsilon bc\]
Where A is the unitless absorbance, Io is the intensity of light entering the sample, It is the intensity of light transmitted out of the sample, b is the path length, c is the concentration of the molecule absorbing the light and \(\epsilon\) is the extinction coefficient and has the units of concentration-1 length-1. The extinction coefficient is often a very large number which allows one to measure very small concentrations of solute, and it is a property of the molecule, but is influenced by the solvent.
Limitations of Beer's Law
Beer's Law is linear over a small range of absorbances and you can not believe all readings a spectrometer gives you. The rule of thumb that we will use in this lab applies only to the spectrometers we use, and that is that we can only trust values between A= 0.05 and A=1.0. There are two types of reasons for nonlinearity, chemical and instrumental.
Instrumental deviations from linearity typically relate to the sensitivity of the detection system (see above). At high absorbances the limit of detectivity may be reached and the detector simply can't "see" the light. At low absorbances the percent transmittance approaches 100% and the detector can't discern a difference.
Chemical reasons for nonlinearity typically involve solutes aggregating at high concentrations, which changes the spectra. That is, the spectrum is a consequence of the energy levels of the molecular orbitals and these are influenced by the surroundings (solvent). At high solute concentrations there is a deviation as the solute molecules begin to interact with each other (in a manner that is different than the solute-solvent interaction).
Important Note:
If a solution is too concentrated (A>1) you simply need to dilute it until it is in the correct range and use the dilution factor to back calculate the original concentration. So if you had an unknown with A=3, diluted it 10 fold 3 times so that A was between 0.05 and 1, your sample is now 1/1000 the concentration of the original. You then calculate from Beer's law the concentration of your diluted unknown, and the original sample is 1,000 times that.
One of the advantages of spectroscopy is that it allows one to measure dilute solutions, and it is always easy to dilute a concentrated solution (simply add solvent), and so if the absorbance is greater than one, all you have to do is dilute the solution.
In this class we are using the range of 0.05 to 1.0 as a "rule of thumb", but you can take a more concentrated solution, dilute it several times, and see if you still have a linear function. The sensitivity of the photo detectors is not uniform across all wavelengths and you may find that at some wavelengths the system works at absorbances greater than 1, while at others it does not. To be safe, use this range, or make a Beer's law plot and see if it is linear.
SpectraVis
In this lab we will use the SpectraVis spectrometer by Vernier, which you can either run off your laptop or with the LabQuest device supplied in the lab. Please go to the SpectroVis user manual for details on how to run the spectrometer on your device, and contact your instructor if you wish to use the LoggerPro software.
Calibrate
- Warm spectrometer for 5 minutes
- Fill cuvette 3/4ths full of solvent, cap and place in cuvette cavity so the light path goes through the clear side
- From Experiment menu choose Spectrophotometer/calibrate
- Follow the instructions until the calibration is OK.
Generate a Spectrum
- Calibrate spectrometer with pure solvent
- Fill cuvette 3/4 full with analyte (solution being investigated)
- Click <Collect> and once the spectrum is displayed click <Stop>
- To store spectrum go to the experiment menu and choose "Store Latest Run"
- Save as csv to a flashdrive
Generate a Beer's Law Plot
- Calibrate spectrometer with pure solvent
- Generate a spectrum (above) of the most concentrated solution
- click "configure spectrometer data collection"
- Select Absorbance
- Pick a wavelength where A is approximately 1, record it and the concentration.
- Repeat with the other samples recording the absorbance at the same wavelength


