7.6: Aromaticity and the Hückel 4n + 2 Rule
- Page ID
- 469410
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
In 1931, German chemist and physicist Erich Hückel proposed a theory to help determine if a planar ring molecule would have aromatic properties. His rule states that if a cyclic, planar molecule has \(4n+2\) \(π\) electrons, it is considered aromatic. This rule would come to be known as Hückel's Rule.
Four Criteria for Aromaticity
When deciding if a compound is aromatic, go through the following checklist. If the compound does not meet all the following criteria, it is likely not aromatic.
- The molecule is cyclic (a ring of atoms)
- The molecule is planar (all atoms in the molecule lie in the same plane)
- The molecule is fully conjugated (p orbitals at every atom in the ring)
- The molecule has 4n+2 π electrons (n=0 or any positive integer)
Counting π Electrons?
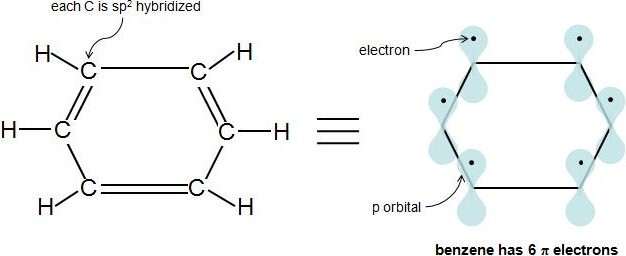
Perhaps the toughest part of Hückel's Rule is figuring out which electrons in the compound are actually π electrons. Once this is figured out, the rule is quite straightforward. Pi electrons lie in the p orbitals and sp2 hybridized atoms have 1 of these p orbitals each. When looking at a C=C double bond we know that there is one sigma bond and one pi bond. The pi bond is formed by the overlap of 1 p orbital from each carbon in the double bond. Each p orbital contains one electron so when the two p orbitals overlap the two electrons become a pi bond and are thus called pi electrons. Because aromaticity deals directly with double bonds and conjugation it is simpler to just count the number pi electrons in a compound. Each double bond (π bond) always contributes 2 π electrons. Benzene has 3 double bonds, so it has 6 π electrons.
Why 4n+2 π Electrons?
According to Hückel's Molecular Orbital Theory, a compound is particularly stable if all of its bonding molecular orbitals are filled with paired electrons. This is true of aromatic compounds, meaning they are quite stable. With aromatic compounds, 2 electrons fill the lowest energy molecular orbital, and 4 electrons fill each subsequent energy level (the number of subsequent energy levels is denoted by n), leaving all bonding orbitals filled and no anti-bonding orbitals occupied. This gives a total of 4n+2 \(\pi\) electrons. You can see how this works with the molecular orbital diagram for the aromatic compound, benzene, below. Benzene has 6 \(\pi\) electrons. Its first 2 \(\pi\) electrons fill the lowest energy orbital, and it has 4 \(\pi\) electrons remaining. These 4 fill in the orbitals of the succeeding energy level. Notice how all of its bonding orbitals are filled, but none of the anti-bonding orbitals have any electrons.
.jpg?revision=1&size=bestfit&width=317&height=292)
To apply the 4n+2 rule, first count the number of π electrons in the molecule. Then, set this number equal to 4n+2 and solve for n. If is 0 or any positive integer (1, 2, 3,...), the rule has been met. For example, benzene has six \(\pi\) electrons:
\[\begin{align} 4n + 2 &= 6 \\ 4n &= 4 \\ n &= 1 \end{align} \nonumber \]
For benzene, we find that \(n=1\), which is a positive integer, so the rule is met.
With Hückel's theory we can assume that if a molecule meets the other criteria for aromaticity and also has 2, 6, 10, 14, 18 ect. pi electrons it will most likely be aromatic.
Antiaromaticity
More than 100 years ago, chemists recognized the possible existence of other conjugated cyclic polyalkenes, which at least superficially would be expected to have properties like benzene. The most interesting of these are cyclobutadiene, whose shape and alignment of p orbitals suggested it should have substantial electron-delocalization energies.
Cyclobutadiene
However, cyclobutadiene was found to be an extremely unstable molecules. In fact, cyclobutadiene is even more reactive than most alkenes. The synthesis of cyclobutadiene eluded chemists for almost 100 years. As more work was done, it became increasingly clear that the molecule, when formed in reactions, was immediately converted to something else. Finally, cyclobutadiene was captured in an essentially rigid matrix of argon at 8K. On warming to even 35K , it dimerizes through a Diels Alder reaction to yield a tricyclicdiene.

Due to the square ring, cyclobutadiene was expected to have some degree of destabilization associated with ring strain. However, estimations of the strain energies, though substantial, did not account for cyclobutadiene's high degree of instability. Also, why was it not being stabilized through cyclic conjugation in the same way as benzene. The answer can be seen in the molecular orbitals.
We considering the molecular orbitals diagram of the analogous 1,3-butadiene, the four 2p atomic orbitals combine to form four pi molecular orbitals of increasing energy. Two bonding pi orbitals and two antibonding pi* orbitals. The 4 pi electrons of 1,3-butadiene completely fill the bonding molecular orbitals giving is the additional stability associated with conjugated double bonds.

However, when placed into a ring the molecular orbitals undergo a significant change. The four p orbitals of cyclobutadiene combine to form the following 4 molecular orbitals:
- a bonding molecular orbital which is lower in energy than the atomic orbitals
- two degenerate non-bonding molecular orbitals which are of equivalent energy to the atomic orbitals
- one antibonding molecular orbital which is higher in energy
The non-bonding orbitals represent that there is no direct interaction between adjacent atoms. When adding cyclobutadiene's 4 pi electrons to the molecular orbital diagram, the bonding orbital is filled and both non-bonding orbitals are singly occupied. If cyclobutadiene's double bonds were delocalized, all the pi electrons would be in low energy bonding orbitals. However, only two of the pi electrons are in bonding orbitals; the other two are non-bonding. In addition, the molecular orbital diagram shows that two of the electrons are unpaired, a situation called a triplet state, which usually makes organic molecules very reactive. For cyclobutadiene cyclic conjugation has made the molecule less stable. This unexpected instability in 4n π-electron cyclic conjugated compounds is termed antiaromaticity and the compounds are called antiaromatic.
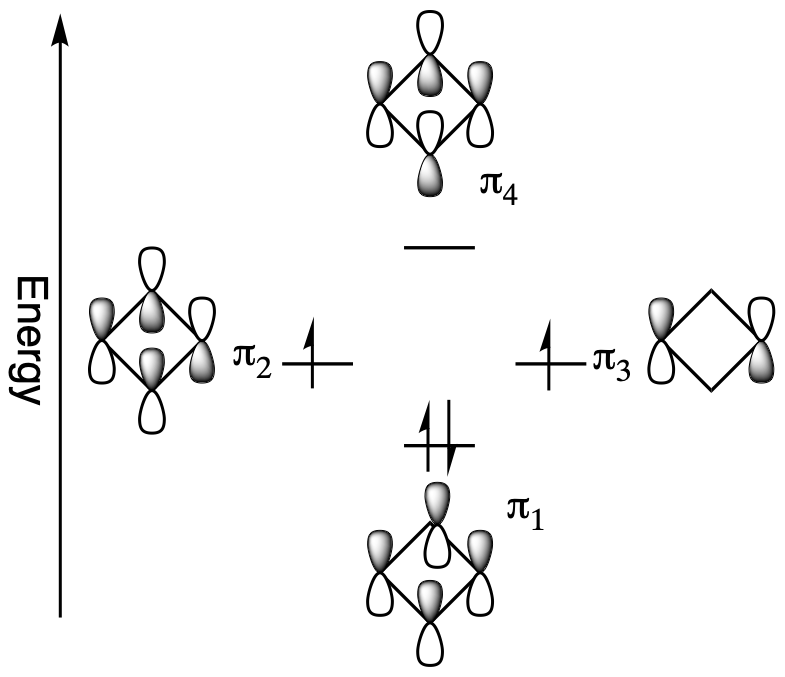
Antiaromaticity gives cyclobutadiene some interesting structural features. Cyclobutadiene's single and double bonds have different bond lengths, 158 pm and 135 pm respectively which give it a rectangular shape. If the double bonds were conjugated, there would only be one average bond length, like benzene, and shape would be square. In fact, cyclobutadiene's double bonds are not conjugated but locked into position.
Just like 4n + 2 rule with aromaticity, compounds which are flat, cyclic, have a p orbital at every member of the ring, and 4n pi electrons should be antiaromatic. Another potentially antiaromatic molecule is 1,3,5,7-cyclooctatetraene.
Cyclooctatetraene was first synthesized in 1911 by a German chemist, R. Willstatter (Nobel Prize 1915), who reported an extraordinary thirteen-step synthesis of cyclooctatetraene from a rare alkaloid called pseudopelletierine isolated from the bark of pomegranate trees. However, during the Second World War, the German chemist W. Reppe found that cyclooctatetraene can be made in reasonable yields by the tetramerization of ethyne under the influence of a nickel cyanide catalyst:

If cyclooctatetraene was flat it would have all the requirements to be antiaromatic. It is cyclic, has a p orbital in every member of the ring, and has 8 pi electrons. When looking at the molecular orbital diagram of cyclooctatetraene we see it shares certain characteristics in common with cyclobutadiene. Two of the molecular orbitals are degenerate non-bonding orbitals. When the molecular orbitals are fill with cyclooctatetraene's 8 pi electrons the last two electrons are unpaired in the two nonbonding orbitals creating a triplet state. Based off the molecular orbital diagram cyclooctatetraene should be antiaromatic.
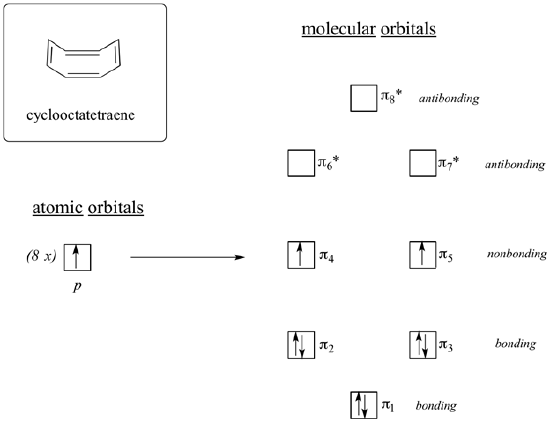
However, cyclooctatetraene is easily prepared and relatively stable. Also, it undergoes addition reactions typical of alkenes. In reality, cyclooctatetraene is not flat but has a tub-like shape. By assuming this shape, the p orbtials between double bond are out of alignment for overlap. Because the double bonds are not conjugated, cyclooctatetraene escapes the destabilizing effects of antiaromaticity. This makes its its pi bonds react like 'normal' alkenes. Because cyclooctatetraene is not flat nor conjugated it is properly defined as non-aromatic. In general, if an antiaromatic compound has the ability to form a non-planar shape it will do so to avoid destabilization by becoming non-aromatic.
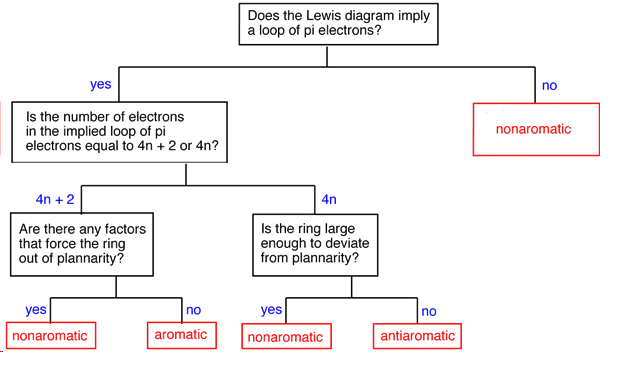
Determining if a Compound is Aromatic, Antiaromatic, or Nonaromatic
To make this determination it is important to first as if the compound has the possibility of cyclic conjugation. This requires that the compound be cyclic and have a p orbital at every atom in the ring. If the compound does not have both of these criteria it cannot be aromatic or antiaromatic and must therefore be nonaromatic. Next the number of pi electrons in the ring is determined to see if it follows the count of aromaticity (4n + 2) or antiaromaticity (4n). Before making the final determination, it is vital to know the actual geometry of the molecule. Despite the number of pi electrons, a compound cannot be aromatic or antiaromatic if its geometry is not planar to allow for p orbital overlap.
A very common misconception is that hybridization can be used to predict the geometry, or that hybridization somehow involves an energy cost associated with 'promoting' electrons into the hybrid orbitals. This is entirely wrong. Hybridization is always determined by geometry. You can only assign hybridization states to an atom if you already know its geometry, based on some experimental or theoretical evidence. The geometry of the oxygen in furan is trigonal planar and therefore the hybridization must be sp2.
The specific rule is that if you have an sp2 conjugated system, the lone pair will be involved if it makes the system more stable. In this case, conferring Hückel 4n+2 aromaticity. For furan with two lone pairs on the oxygen atom, if we count electrons from the carbon atoms, we have 4 (one per carbon). So adding two electrons from one of the lone pairs will give 6 = 4(1)+2, so Hückel rule is applicable and furan is aromatic.


.jpg?revision=1)