7.3: Kinetic vs. Thermodynamic Control of Reactions

Like non-conjugated dienes, conjugated dienes are subject to attack by electrophiles. In fact, conjugated dienes experience relatively greater kinetic reactivity when reacted with electrophiles than non-conjugated dienes do. The reaction mechanism is similar to other electrophilic addition reactions to alkenes. During the electrophilic addition of HBr to a 1,3-butadiene, However, there are two possible outcomes once the carbocation intermediate is formed. The allyl carbocation is stabilized by resonance structures that vary in the position of the carbocation. This allows the bromide ion to add to either of these carbons resulting in the formation 1,2 and 1,4 addition products. When this reaction is run at a temperature of 0 ^oC or lower, the 1,2 addition product dominates. However, if the same reaction is run at 40 ^oC the 1,4 addition product dominates.

The reaction of one equivalent of hydrogen bromide with 1,3-butadiene yields different product ratios under different reaction conditions and is a classic example of the concept of thermodynamic versus kinetic control of a reaction.

At lower temperatures the formation of the 1,2 and 1,4 addition products are irreversible and thus do not reach equilibrium. When a reaction is irreversible the major product is determined by the relative reaction rates and not by thermodynamic stability. Of the two products, the formation of the 1,2 addition product has a higher rate of reaction and forms faster making it the major product. The reaction product which forms with a higher rate of reaction is called the Kinetic Product and when the kinetic product dominates, the reaction is said to be under Kinetic Control.

At higher temperatures the reaction to form both products becomes reversible and a reaction equilibrium is reached. When a reaction is reversible the major product is determined by thermodynamic stability. The 1,4 addition product is more stable and becomes the major product under these reaction conditions. The more stable product is called the Thermodynamic Product and when the thermodynamic product dominates, the reaction is said to be under Thermodynamic Control.

The 1,4 addition product is more stable because it has an internal, disubstituted double bond, and we know that as a general rule that the thermodynamic stability of an alkene increases with increasing substitution. So, when compared to the terminal, monosubstituted alkene of the 1,2 addition product, the 1,4 addition product is expected to be more stable.

A simple definition is that the kinetic product is the product that is formed faster, and the thermodynamic product is the product that is more stable. This is precisely what is happening here. The kinetic product is 3-bromobut-1-ene, and the thermodynamic product is 1-bromobut-2-ene (specifically, the trans isomer).

An explanation for the temperature influence is shown in the following energy diagram for the addition of HBr to 1,3-butadiene. The initial step in which a proton bonds to carbon #1 is the rate determining step, as indicated by the large activation energy (light gray arrow). The second faster step is the product determining step, and there are two reaction paths (colored blue for 1,2-addition and magenta for 1,4-addition).

At elevated temperatures, the products are more likely to have enough energy to overcome the reverse activation barrier for the second step allowing regeneration of the carbocation intermediate. Under these conditions, this step of the mechanism will be reversible and an equilibrium will be established. Since the system is no longer limited by temperature, the system will minimize its Gibbs free energy, which is the thermodynamic criterion for chemical equilibrium. This places the reaction under thermodynamic control and the most thermodynamically stable molecule, the 1,4 addition product, will be predominantly formed.

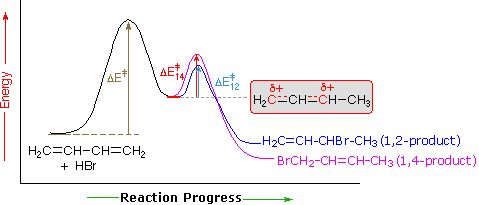
If the reaction temperature is kept sufficiently low, the products will not have enough energy to overcome the reverse activation barrier to regenerate the carbocation intermediate making this step of the mechanism effectively irreversible. This reaction is under kinetic control meaning the product which forms faster, the kinetic product, will predominate.

Of the two reaction pathways, the 1,2-addition has a smaller activation energy and would be expected to have a higher reaction rate than the 1,4-addition. The high reaction rate for 1,2-addition can be attributed to the formation of an ion pair during the reaction mechanism. This means that, after a double bond is protonated, the halide counterion remains in close proximity to the carbocation generated. Immediately following dissociation of HX, the chloride ion is going to be much closer to C−2 than it is to C−4, and therefore attack at C−2 is much faster. This ion pair mechanism is a pre-exponential constant effects that is attributed to the proximity and frequency of collision rather than a activation barrier effect.

Experimental Evidence for the Ion-Pair Mechanism

In 1979, Nordlander et al. carried out a similar investigation on the addition of DCl (deuterated hydrochloric acid) to a different substrate, 1,3-pentadiene. This experiment was ingenious, because it was designed to proceed via an almost symmetrical intermediate:

Resonance forms 7a and 7b are both allylic and secondary. There is a very minor difference in their stabilities arising from the different hyperconjugative ability of C-D vs C-H bonds, but in any case, it is not very large. Therefore, if we adopt the explanation in the previous section, one would expect there not to be any major kinetic pathway, and both 1,2- and 1,4-addition products (8 and 9) would theoretically be formed roughly equally.

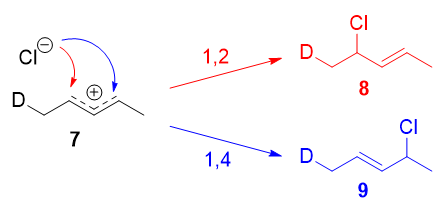
Instead, it was found that the 1,2-addition product was favored over the 1,4-addition product. For example, at -78^oC in the absence of solvent, there was a roughly (75:25) ratio of 1,2- to 1,4-addition products. Clearly, there is a factor that favors 1,2-addition that does not depend on the electrophilicity of the carbon being attacked! The authors attributed this effect to an ion pair mechanism. This means that, after the double bond is protonated (deuterated in this case), the chloride counterion remains in close proximity to the carbocation generated. Immediately following dissociation of DCl, the chloride ion is going to be much closer to C-2 than it is to C-4, and therefore attack at C-2 is much faster. In fact, normal electrophilic addition of HX to conjugated alkenes in polar solvents can also proceed via similar ion pair mechanisms. This is reflected by the greater proportion of syn addition products to such substrates.