Chiral Molecules
The term chiral, from the Greek work for 'hand', refers to anything which cannot be superimposed on its own mirror image. Certain organic molecules are chiral meaning that they are not superimposable on their mirror image. Chiral molecules contain one or more stereocenters, which are almost always tetrahedral (sp3-hybridized) carbons with four different substituents. Consider the molecule A below: a tetrahedral carbon, with four different substituents denoted by balls of four different colors. Try to build these molecules exactly as they are drawn using your molecular models. It will be much easier to see the mirror plane as well as see their chiral nature using molecular models.

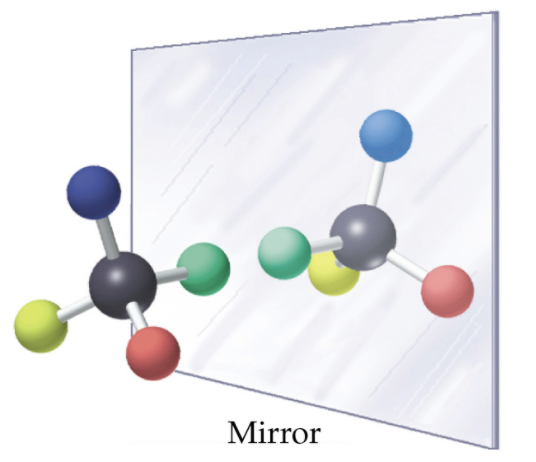
The mirror image of A, which we will call B, is drawn on the right side of the figure, and an imaginary mirror is in the middle. Notice that every point on A lines up through the mirror with the same point on B: in other words, if A looked in the mirror, it would see B looking back.
Now, if we flip compound A over and try to superimpose it point for point on compound B, we find that we cannot do it: if we superimpose any two colored balls, then the other two are misaligned.

A is not superimposable on its mirror image (B), thus by definition A is a chiral molecule. It follows that B also is not superimposable on its mirror image (A), and thus it is also a chiral molecule.
A and B are called stereoisomers or optical isomers: molecules with the same molecular formula and the same bonding arrangement, but a different arrangement of atoms in space. Enantiomers are pairs of stereoisomers which are mirror images of each other: thus, A and B are enantiomers. It should be self-evident that a chiral molecule will always have one (and only one) enantiomer: enantiomers come in pairs. Enantiomers have identical physical properties (melting point, boiling point, density, and so on). However, enantiomers do differ in how they interact with polarized light (we will learn more about this soon) and they may also interact in very different ways with other chiral molecules - proteins, for example. We will begin to explore this last idea in later in this chapter, and see many examples throughout the remainder of our study of biological organic chemistry.
The Many Synonyms of the Stereocenter
Be aware - all of the following terms can be used to describe a stereocenter:
chiral carbon = asymmetric carbon = optically active carbon = stereo carbon = stereocenter = chiral center
Let's apply our chirality discussion to real molecules.
Consider 2-butanol, drawn in two dimensions below.

Carbon #2 is a stereocenter: it is sp3-hybridized and tetrahedral (even though it is not drawn that way above), and the four substituents attached to is are different: a hydrogen (H) , a methyl (-CH3) group, an ethyl (-CH2CH3) group, and a hydroxyl (OH) group. If the bonding at C2 of 2-butanol is drawn in three dimensions and this structure called A. Then the mirror image of A can be drawn to form structure B.

When we try to superimpose A onto B, we find that we cannot do it. Because structure A and B are not superimposable on their mirror image they are both chiral molecules. Because A and B are different due only to the arrangement of atoms in space they are stereoisomers. Because A and B are mirror images of each other they are also enantiomers. When looking at simplified line structures is clear that there are two distinct ways of drawing 2-butanol which only differ in their spatial arrangement around a chiral carbon.

The 3D Structures of the Two Enantiomers of 2-Butanol
For comparison, 2-propanol, is an achiral molecule because is lacks a stereocenter. Carbon #2 is bonded to two identical substituents (methyl groups), and so it is not a stereocenter. Being achiral means that 2-propanol should be superimposable on its mirror image which is shown in the figure below. A more detailed explanation on why 2-propanol is achiral will be given in the next section.
2-propanol is achiral:

Stereoisomers
Stereoisomers have been defined as molecules with the same connectivity but different arrangements of the atoms in space. It is important to note that there are two types of stereoisomers: geometric and optical.
Optical isomers are molecules whose structures are mirror images but cannot be superimposed on one another in any orientation. Optical isomers have identical physical properties, although their chemical properties may differ in asymmetric environments. Molecules that are nonsuperimposable mirror images of each other are said to be chiral.
Geometric isomers differ in the relative position(s) of substituents in a rigid molecule. Simple rotation about a C–C σ bond in an alkene, for example, cannot occur because of the presence of the π bond. The substituents are therefore rigidly locked into a particular spatial arrangement. Thus a carbon–carbon multiple bond, or in some cases a ring, prevents one geometric isomer from being readily converted to the other. The members of an isomeric pair are identified as either cis or trans, and interconversion between the two forms requires breaking and reforming one or more bonds. Because their structural difference causes them to have different physical and chemical properties, cis and trans isomers are actually two distinct chemical compounds.mers have the same connectivity, but different arrangements of atoms in space.
Exercise \(\PageIndex{1}\)
Identify the following molecules as chiral or achiral.

- Answer
-
a) chiral (4 different groups off C)
b) achiral (2 identical -CH3 substituents off central C)
c) achiral (2 identical -CH2CH3 substituents off central C)
d) achiral (2 identical CH3 substituents off carbon 2)
e) chiral (4 different groups off carbon 2)
f) achiral (2 identical CH3 substituents off central C)
Exercise \(\PageIndex{2}\)
Determine if the following sets of compounds in each group are enantiomers or the same compound.

- Answer
-
a) enantiomers – non superimposable mirror images
b) same compound – when you rotate the molecule on the right it is identical to the one on the left
c) enantiomers – non superimposable mirror images
d) enantiomers – non superimposable mirror images


