6.3: Lattice Structures in Crystalline Solids
- Last updated
- Save as PDF
- Page ID
- 488977
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Learning Objectives
- Describe the arrangement of atoms and ions in crystalline structures
- Compute ionic radii using unit cell dimensions
- Explain the use of X-ray diffraction measurements in determining crystalline structures
Over 90% of naturally occurring and man-made solids are crystalline. Most solids form with a regular arrangement of their particles because the overall attractive interactions between particles are maximized, and the total intermolecular energy is minimized, when the particles pack in the most efficient manner. The regular arrangement at an atomic level is often reflected at a macroscopic level. In this module, we will explore some of the details about the structures of metallic and ionic crystalline solids, and learn how these structures are determined experimentally.
The Structures of Metals
We will begin our discussion of crystalline solids by considering elemental metals, which are relatively simple because each contains only one type of atom. A pure metal is a crystalline solid with metal atoms packed closely together in a repeating pattern. Some of the properties of metals in general, such as their malleability and ductility, are largely due to having identical atoms arranged in a regular pattern. The different properties of one metal compared to another partially depend on the sizes of their atoms and the specifics of their spatial arrangements. We will explore the similarities and differences of four of the most common metal crystal geometries in the sections that follow.
Unit Cells of Metals
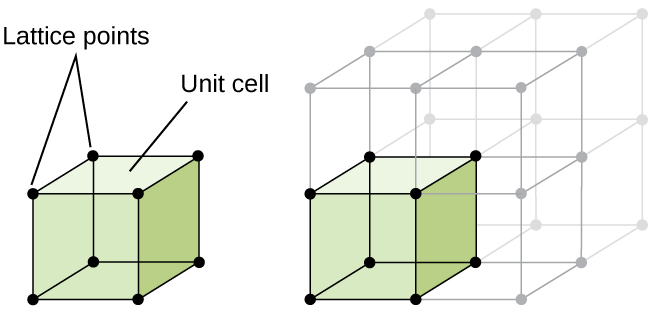
The structure of a crystalline solid, whether a metal or not, is best described by considering its simplest repeating unit, which is referred to as its unit cell. The unit cell consists of lattice points that represent the locations of atoms or ions. The entire structure then consists of this unit cell repeating in three dimensions, as illustrated in Figure \(\PageIndex{1}\).
Let us begin our investigation of crystal lattice structure and unit cells with the most straightforward structure and the most basic unit cell. To visualize this, imagine taking a large number of identical spheres, such as tennis balls, and arranging them uniformly in a container. The simplest way to do this would be to make layers in which the spheres in one layer are directly above those in the layer below, as illustrated in Figure \(\PageIndex{2}\). This arrangement is called simple cubic structure, and the unit cell is called the simple cubic unit cell or primitive cubic unit cell.
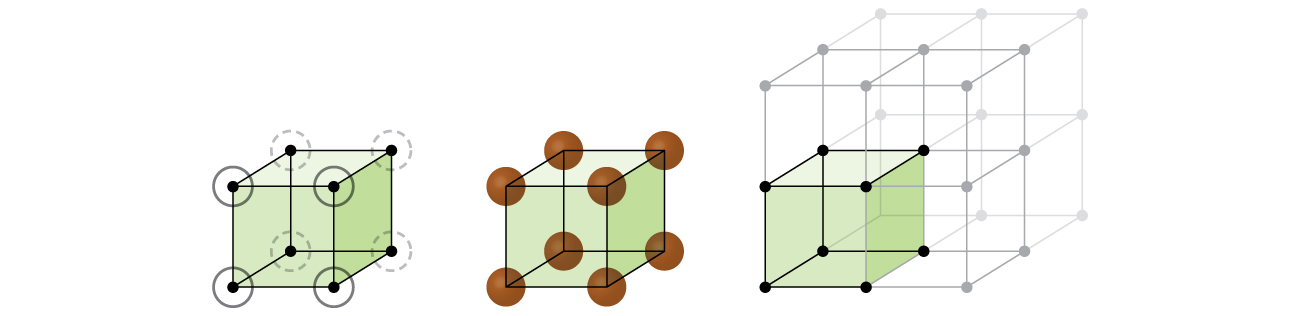
In a simple cubic structure, the spheres are not packed as closely as they could be, and they only “fill” about 52% of the volume of the container. This is a relatively inefficient arrangement, and only one metal (polonium, Po) crystallizes in a simple cubic structure. As shown in Figure \(\PageIndex{3}\), a solid with this type of arrangement consists of planes (or layers) in which each atom contacts only the four nearest neighbors in its layer; one atom directly above it in the layer above; and one atom directly below it in the layer below. The number of other particles that each particle in a crystalline solid contacts is known as its coordination number. For a polonium atom in a simple cubic array, the coordination number is, therefore, six.
 " height="200" width="463" src="/@api/deki/files/61021/CNX_Chem_10_06_SimpleCub2.jpg">
" height="200" width="463" src="/@api/deki/files/61021/CNX_Chem_10_06_SimpleCub2.jpg">
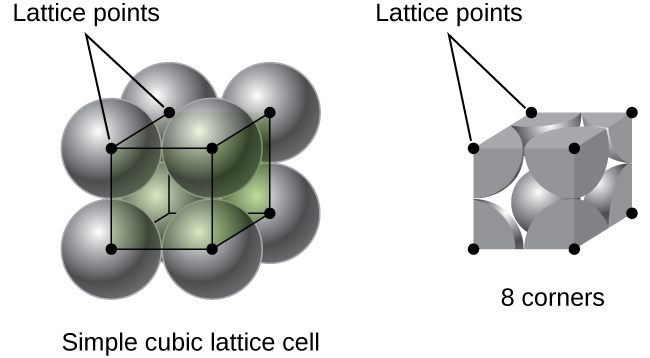
In a simple cubic lattice, the unit cell that repeats in all directions is a cube defined by the centers of eight atoms, as shown in Figure \(\PageIndex{4}\). Atoms at adjacent corners of this unit cell contact each other, so the edge length of this cell is equal to two atomic radii, or one atomic diameter. A cubic unit cell contains only the parts of these atoms that are within it. Since an atom at a corner of a simple cubic unit cell is contained by a total of eight unit cells, only one-eighth of that atom is within a specific unit cell. And since each simple cubic unit cell has one atom at each of its eight “corners,” there is \(8×\dfrac{1}{8}=1\) atom within one simple cubic unit cell.
Example \(\PageIndex{1}\): Calculating Atomic Radius and Density for Metals (Part 1)
The edge length of the unit cell of alpha polonium is 336 pm.
- Determine the radius of a polonium atom.
- Determine the density of alpha polonium.
Solution
Alpha polonium crystallizes in a simple cubic unit cell:
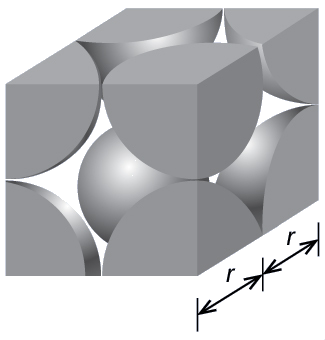
(a) Two adjacent Po atoms contact each other, so the edge length of this cell is equal to two Po atomic radii: \(l = 2r\). Therefore, the radius of Po is
\[r=\mathrm{\dfrac{l}{2}=\dfrac{336\: pm}{2}=168\: pm}\nonumber \]
(b) Density is given by
\[\mathrm{density=\dfrac{mass}{volume}}.\nonumber \]
The density of polonium can be found by determining the density of its unit cell (the mass contained within a unit cell divided by the volume of the unit cell). Since a Po unit cell contains one-eighth of a Po atom at each of its eight corners, a unit cell contains one Po atom.
The mass of a Po unit cell can be found by:
\[\mathrm{1\: Po\: unit\: cell×\dfrac{1\: Po\: atom}{1\: Po\: unit\: cell}×\dfrac{1\: mol\: Po}{6.022\times 10^{23}\:Po\: atoms}×\dfrac{208.998\:g}{1\: mol\: Po}=3.47\times 10^{−22}\:g}\nonumber \]
The volume of a Po unit cell can be found by:
\[V=l^3=\mathrm{(336\times 10^{−10}\:cm)^3=3.79\times 10^{−23}\:cm^3}\nonumber \]
(Note that the edge length was converted from pm to cm to get the usual volume units for density.)
Therefore, the density of
\[\mathrm{Po=\dfrac{3.471\times 10^{−22}\:g}{3.79\times 10^{−23}\:cm^3}=9.16\: g/cm^3}\nonumber \]
Exercise \(\PageIndex{1}\)
The edge length of the unit cell for nickel is 0.3524 nm. The density of Ni is 8.90 g/cm3. Does nickel crystallize in a simple cubic structure? Explain.
- Answer
-
No. If Ni were simple cubic, its density would be given by:
\[\mathrm{1\: Ni\: atom×\dfrac{1\: mol\: Ni}{6.022\times 10^{23}\:Ni\: atoms}×\dfrac{58.693\:g}{1\: mol\: Ni}=9.746\times 10^{−23}\:g}\nonumber \]
\[V=l^3=\mathrm{(3.524\times 10^{−8}\:cm)^3=4.376\times 10^{−23}\:cm^3}\nonumber \]
Then the density of Ni would be
\[(\mathrm{=\dfrac{9.746\times 10^{−23}\:g}{4.376\times 10^{−23}\:cm^3}=2.23\: g/cm^3}\nonumber \]
Since the actual density of Ni is not close to this, Ni does not form a simple cubic structure.
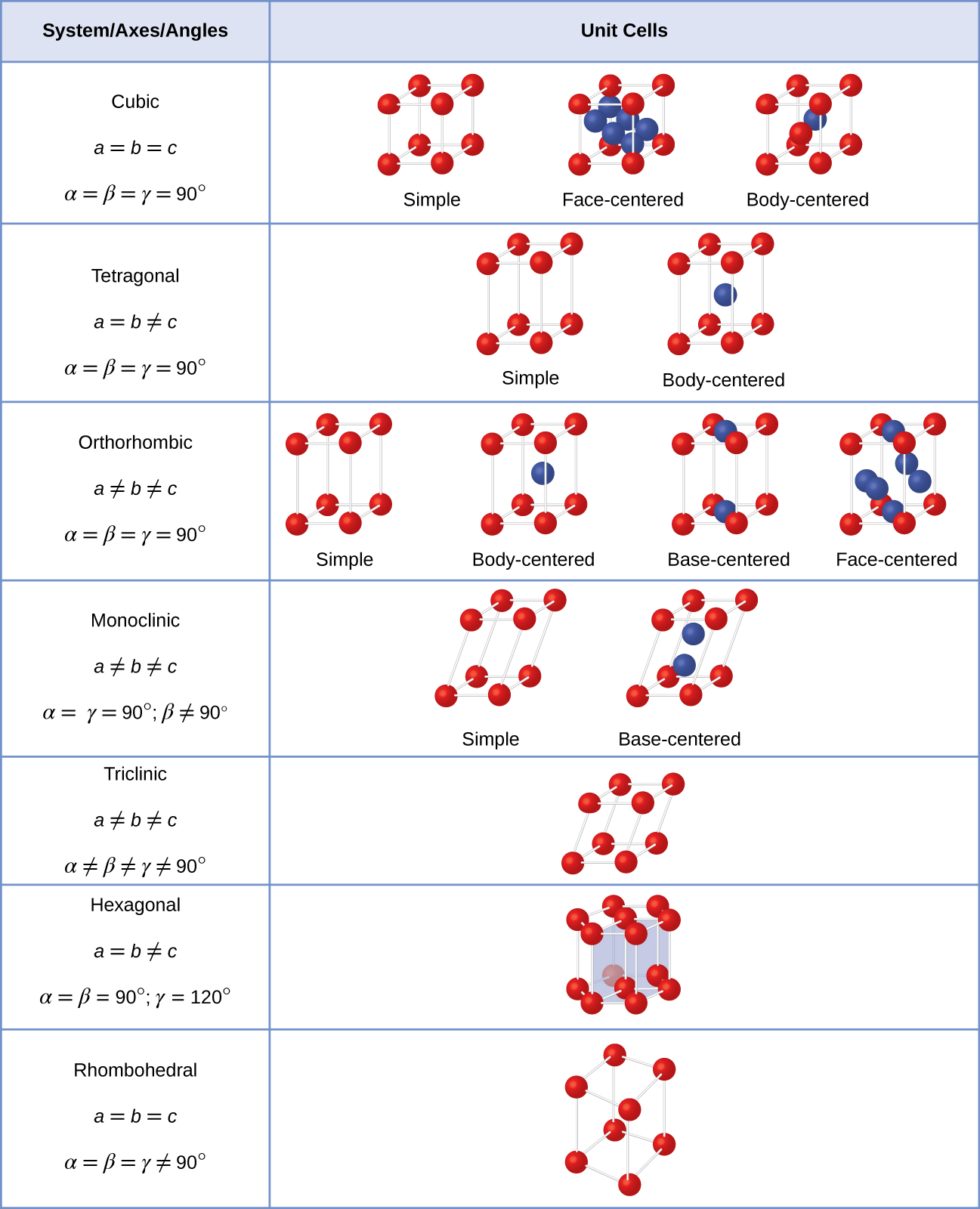
Most metal crystals are one of the four major types of unit cells. For now, we will focus on the three cubic unit cells: simple cubic (which we have already seen), body-centered cubic unit cell, and face-centered cubic unit cell—all of which are illustrated in Figure \(\PageIndex{5}\). (Note that there are actually seven different lattice systems, some of which have more than one type of lattice, for a total of 14 different types of unit cells. We leave the more complicated geometries for later in this module.)
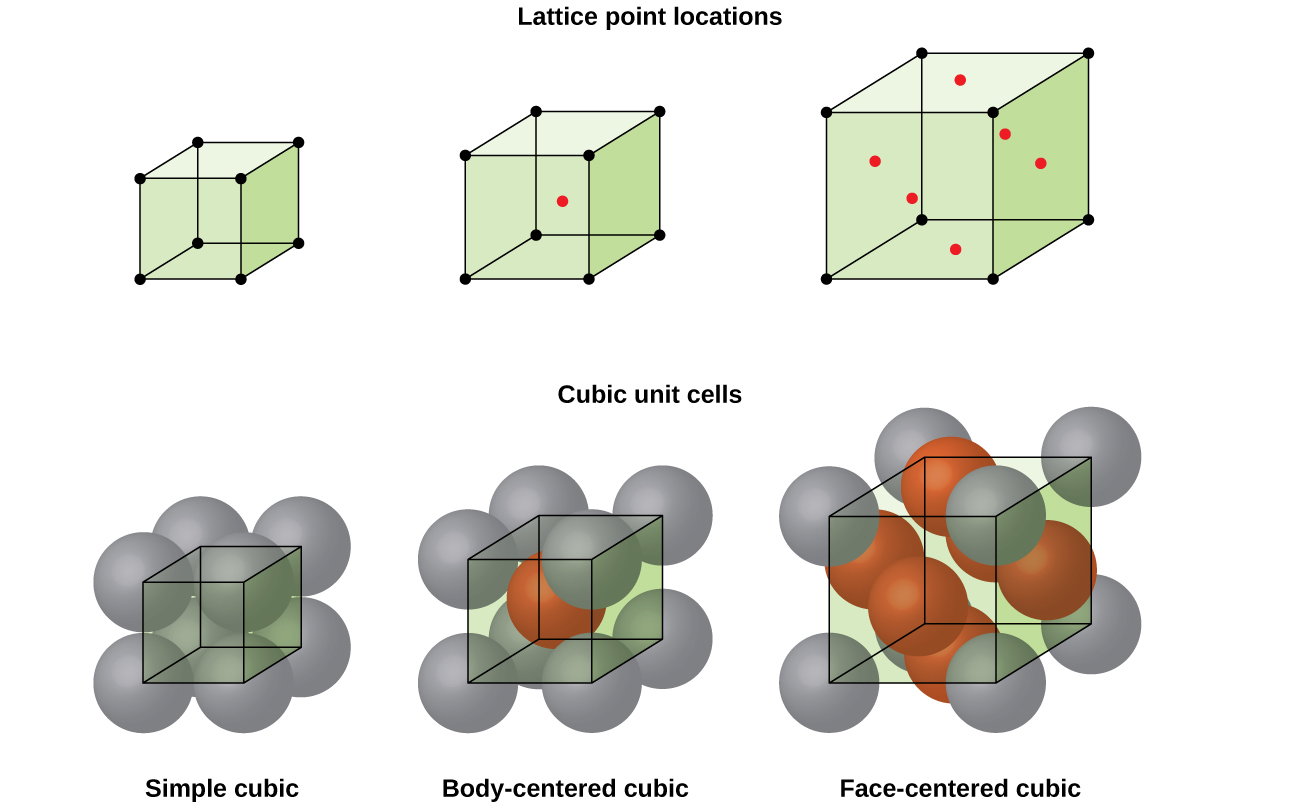
Some metals crystallize in an arrangement that has a cubic unit cell with atoms at all of the corners and an atom in the center, as shown in Figure \(\PageIndex{6}\). This is called a body-centered cubic (BCC) solid. Atoms in the corners of a BCC unit cell do not contact each other but contact the atom in the center. A BCC unit cell contains two atoms: one-eighth of an atom at each of the eight corners (\(8×\dfrac{1}{8}=1\) atom from the corners) plus one atom from the center. Any atom in this structure touches four atoms in the layer above it and four atoms in the layer below it. Thus, an atom in a BCC structure has a coordination number of eight.
Atoms in BCC arrangements are much more efficiently packed than in a simple cubic structure, occupying about 68% of the total volume. Isomorphous metals with a BCC structure include K, Ba, Cr, Mo, W, and Fe at room temperature. (Elements or compounds that crystallize with the same structure are said to be isomorphous.)
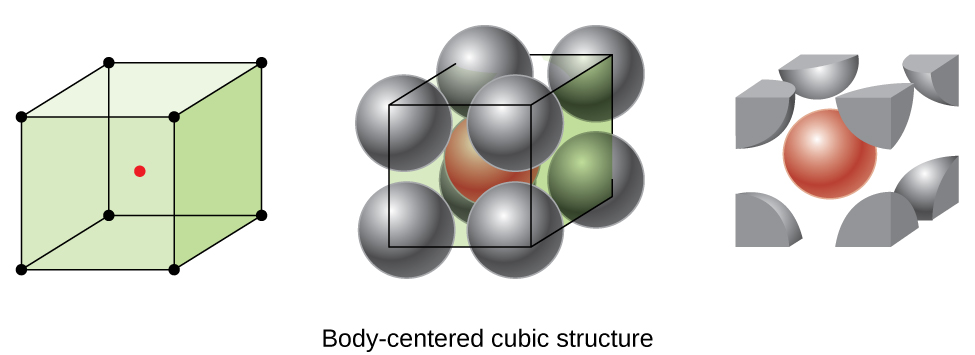
Many other metals, such as aluminum, copper, and lead, crystallize in an arrangement that has a cubic unit cell with atoms at all of the corners and at the centers of each face, as illustrated in Figure \(\PageIndex{7}\). This arrangement is called a face-centered cubic (FCC) solid. A FCC unit cell contains four atoms: one-eighth of an atom at each of the eight corners (\(8×\dfrac{1}{8}=1\) atom from the corners) and one-half of an atom on each of the six faces (\(6×\dfrac{1}{2}=3\) atoms from the faces). The atoms at the corners touch the atoms in the centers of the adjacent faces along the face diagonals of the cube. Because the atoms are on identical lattice points, they have identical environments.
Atoms in an FCC arrangement are packed as closely together as possible, with atoms occupying 74% of the volume. This structure is also called cubic closest packing (CCP). In CCP, there are three repeating layers of hexagonally arranged atoms. Each atom contacts six atoms in its own layer, three in the layer above, and three in the layer below. In this arrangement, each atom touches 12 near neighbors, and therefore has a coordination number of 12. The fact that FCC and CCP arrangements are equivalent may not be immediately obvious, but why they are actually the same structure is illustrated in Figure \(\PageIndex{8}\).
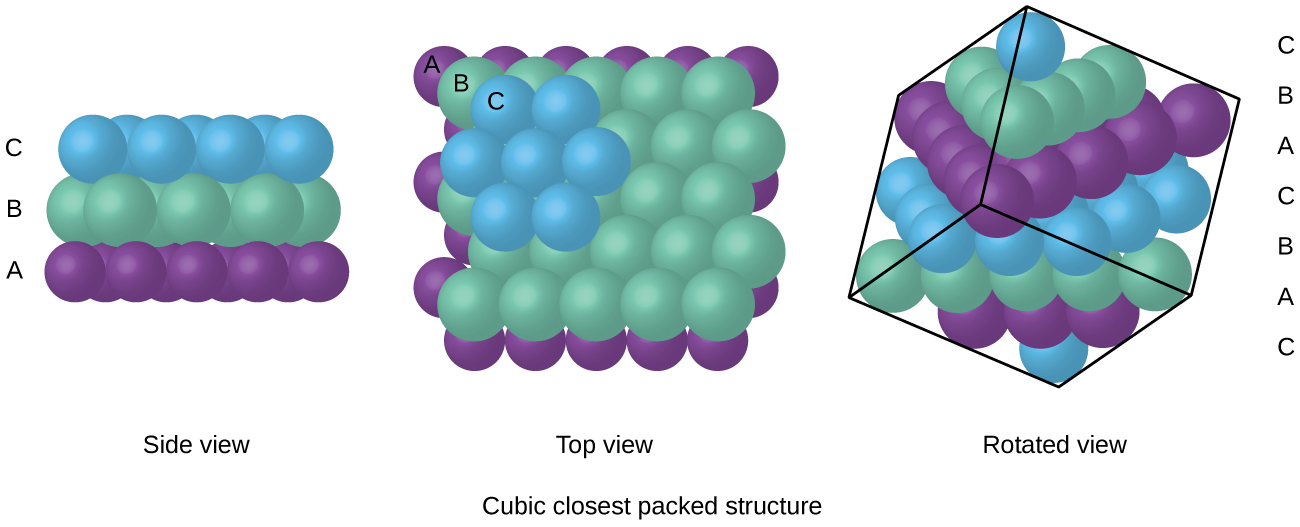
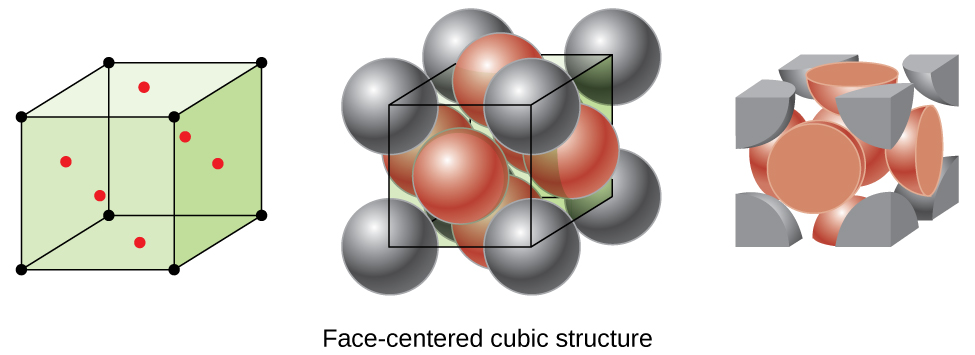
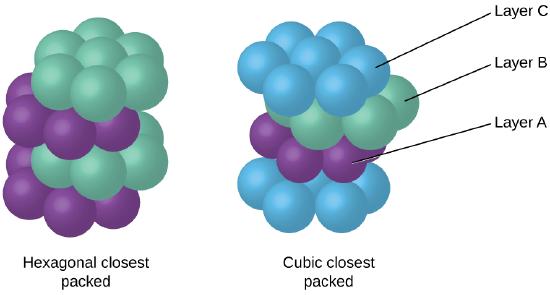
Because closer packing maximizes the overall attractions between atoms and minimizes the total intermolecular energy, the atoms in most metals pack in this manner. We find two types of closest packing in simple metallic crystalline structures: CCP, which we have already encountered, and hexagonal closest packing (HCP) shown in Figure \(\PageIndex{9}\). Both consist of repeating layers of hexagonally arranged atoms. In both types, a second layer (B) is placed on the first layer (A) so that each atom in the second layer is in contact with three atoms in the first layer. The third layer is positioned in one of two ways. In HCP, atoms in the third layer are directly above atoms in the first layer (i.e., the third layer is also type A), and the stacking consists of alternating type A and type B close-packed layers (i.e., ABABAB⋯). In CCP, atoms in the third layer are not above atoms in either of the first two layers (i.e., the third layer is type C), and the stacking consists of alternating type A, type B, and type C close-packed layers (i.e., ABCABCABC⋯). About two–thirds of all metals crystallize in closest-packed arrays with coordination numbers of 12. Metals that crystallize in an HCP structure include Cd, Co, Li, Mg, Na, and Zn, and metals that crystallize in a CCP structure include Ag, Al, Ca, Cu, Ni, Pb, and Pt.
Example \(\PageIndex{2}\): Calculating Atomic Radius and Density for Metals (Part 2)
Calcium crystallizes in a face-centered cubic structure. The edge length of its unit cell is 558.8 pm.
- What is the atomic radius of Ca in this structure?
- Calculate the density of Ca.
Solution
(a) In an FCC structure, Ca atoms contact each other across the diagonal of the face, so the length of the diagonal is equal to four Ca atomic radii (d = 4r).
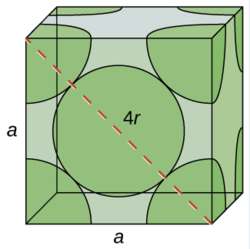
Two adjacent edges and the diagonal of the face form a right triangle, with the length of each side equal to 558.8 pm and the length of the hypotenuse equal to four Ca atomic radii:
\[\begin{align*} a^2+a^2 &=d^2 \\[4pt] \mathrm{(558.8\:pm)^2+(558.5\:pm)^2} &=(4r)^2 \end{align*} \nonumber \]
Solving this gives
\[r=\mathrm{\sqrt{\dfrac{(558.8\:pm)^2+(558.5\:pm)^2}{16}}}=\textrm{197.6 pmg for a Ca radius}. \nonumber \]
(b) Density is given by \(\mathrm{density=\dfrac{mass}{volume}}\). The density of calcium can be found by determining the density of its unit cell: for example, the mass contained within a unit cell divided by the volume of the unit cell. A face-centered Ca unit cell has one-eighth of an atom at each of the eight corners (\(8 \times \dfrac{1}{8}=1\)atom) and one-half of an atom on each of the six faces \(6×\dfrac{1}{2}=3\) atoms), for a total of four atoms in the unit cell.
The mass of the unit cell can be found by:
\[\mathrm{1\: Ca\: unit\: cell×\dfrac{4\: Ca\: atoms}{1\: Ca\: unit\: cell}×\dfrac{1\: mol\: Ca}{6.022\times 10^{23}\:Ca\: atoms}×\dfrac{40.078\:g}{1\: mol\: Ca}=2.662\times 10^{−22}\:g} \nonumber \]
The volume of a Ca unit cell can be found by:
\[V=a^3=\mathrm{(558.8\times 10^{−10}\:cm)^3=1.745\times 10^{−22}\:cm^3} \nonumber \]
(Note that the edge length was converted from pm to cm to get the usual volume units for density.)
Then, the density of polonium:
\[\mathrm{Po=\dfrac{2.662\times 10^{−22}\:g}{1.745\times 10^{−22}\:cm^3}=1.53\: g/cm^3} \nonumber \]
Exercise \(\PageIndex{2}\)
Silver crystallizes in an FCC structure. The edge length of its unit cell is 409 pm.
- What is the atomic radius of Ag in this structure?
- Calculate the density of Ag.
- Answer a
-
144 pm
- Answer b
-
10.5 g/cm3
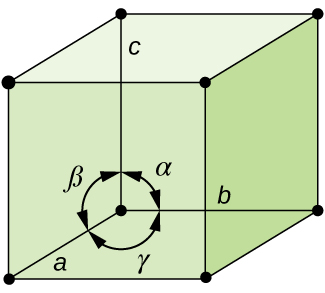
In general, a unit cell is defined by the lengths of three axes (a, b, and c) and the angles (α, β, and γ) between them, as illustrated in Figure \(\PageIndex{10}\). The axes are defined as being the lengths between points in the space lattice. Consequently, unit cell axes join points with identical environments.
There are seven different lattice systems, some of which have more than one type of lattice, for a total of fourteen different unit cells, which have the shapes shown in Figure \(\PageIndex{11}\).
The Structures of Ionic Crystals
Ionic crystals consist of two or more different kinds of ions that usually have different sizes. The packing of these ions into a crystal structure is more complex than the packing of metal atoms that are the same size. Most monatomic ions behave as charged spheres, and their attraction for ions of opposite charge is the same in every direction. Consequently, stable structures for ionic compounds result (1) when ions of one charge are surrounded by as many ions as possible of the opposite charge and (2) when the cations and anions are in contact with each other. Structures are determined by two principal factors: the relative sizes of the ions and the ratio of the numbers of positive and negative ions in the compound.
In simple ionic structures, we usually find the anions, which are normally larger than the cations, arranged in a closest-packed array. (As seen previously, additional electrons attracted to the same nucleus make anions larger and fewer electrons attracted to the same nucleus make cations smaller when compared to the atoms from which they are formed.) The smaller cations commonly occupy one of two types of holes (or interstices) remaining between the anions. The smaller of the holes is found between three anions in one plane and one anion in an adjacent plane. The four anions surrounding this hole are arranged at the corners of a tetrahedron, so the hole is called a tetrahedral hole. The larger type of hole is found at the center of six anions (three in one layer and three in an adjacent layer) located at the corners of an octahedron; this is called an octahedral hole. Figure \(\PageIndex{12}\) illustrates both of these types of holes.
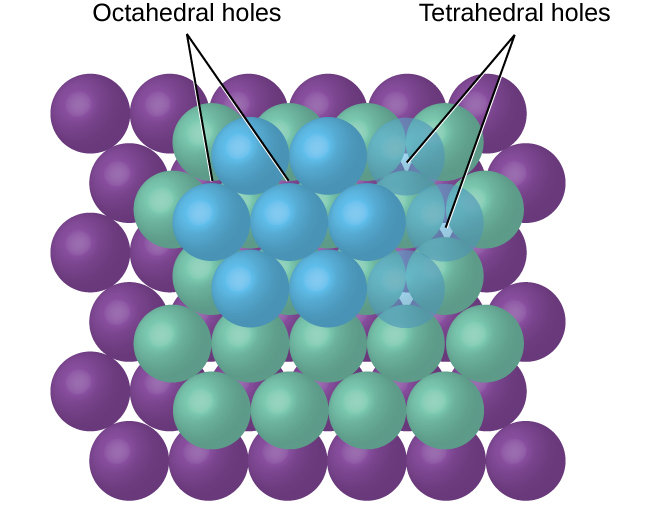
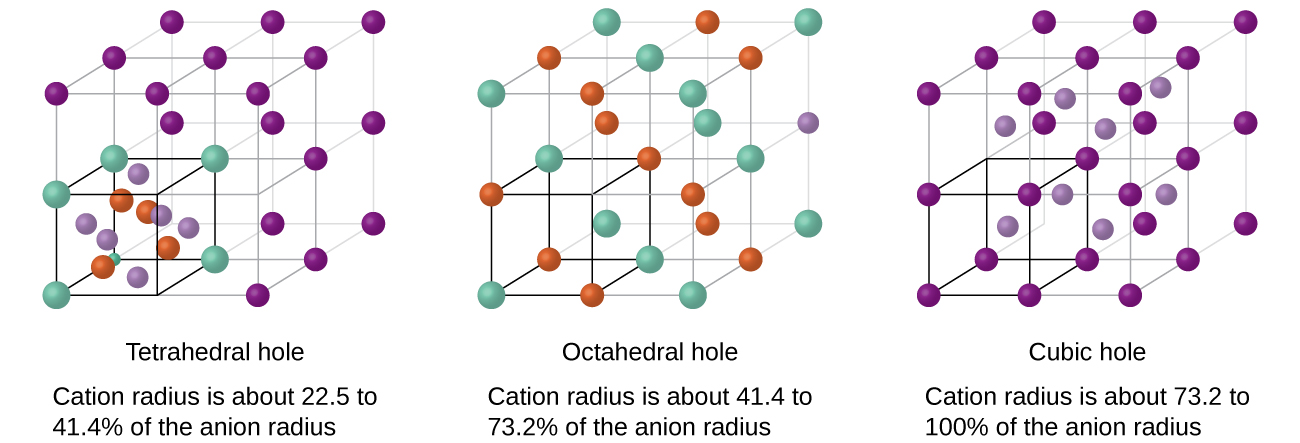
Depending on the relative sizes of the cations and anions, the cations of an ionic compound may occupy tetrahedral or octahedral holes, as illustrated in Figure \(\PageIndex{13}\). Relatively small cations occupy tetrahedral holes, and larger cations occupy octahedral holes. If the cations are too large to fit into the octahedral holes, the anions may adopt a more open structure, such as a simple cubic array. The larger cations can then occupy the larger cubic holes made possible by the more open spacing.
There are two tetrahedral holes for each anion in either an HCP or CCP array of anions. A compound that crystallizes in a closest-packed array of anions with cations in the tetrahedral holes can have a maximum cation:anion ratio of 2:1; all of the tetrahedral holes are filled at this ratio. Examples include Li2O, Na2O, Li2S, and Na2S. Compounds with a ratio of less than 2:1 may also crystallize in a closest-packed array of anions with cations in the tetrahedral holes, if the ionic sizes fit. In these compounds, however, some of the tetrahedral holes remain vacant.
Example \(\PageIndex{3}\): Occupancy of Tetrahedral Holes
Zinc sulfide is an important industrial source of zinc and is also used as a white pigment in paint. Zinc sulfide crystallizes with zinc ions occupying one-half of the tetrahedral holes in a closest-packed array of sulfide ions. What is the formula of zinc sulfide?
Solution
Because there are two tetrahedral holes per anion (sulfide ion) and one-half of these holes are occupied by zinc ions, there must be \(\dfrac{1}{2}×2\), or 1, zinc ion per sulfide ion. Thus, the formula is ZnS.
Exercise \(\PageIndex{3}\): Lithium selenide
Lithium selenide can be described as a closest-packed array of selenide ions with lithium ions in all of the tetrahedral holes. What it the formula of lithium selenide?
- Answer
-
\(\ce{Li2Se}\)
The ratio of octahedral holes to anions in either an HCP or CCP structure is 1:1. Thus, compounds with cations in octahedral holes in a closest-packed array of anions can have a maximum cation:anion ratio of 1:1. In NiO, MnS, NaCl, and KH, for example, all of the octahedral holes are filled. Ratios of less than 1:1 are observed when some of the octahedral holes remain empty.
Example \(\PageIndex{4}\): Stoichiometry of Ionic Compounds Sapphire
Aluminum oxide crystallizes with aluminum ions in two-thirds of the octahedral holes in a closest-packed array of oxide ions. What is the formula of aluminum oxide?
Solution
Because there is one octahedral hole per anion (oxide ion) and only two-thirds of these holes are occupied, the ratio of aluminum to oxygen must be \(\dfrac{2}{3}\):1, which would give \(\mathrm{Al_{2/3}O}\). The simplest whole number ratio is 2:3, so the formula is Al2O3.
Exercise \(\PageIndex{4}\)
The white pigment titanium oxide crystallizes with titanium ions in one-half of the octahedral holes in a closest-packed array of oxide ions. What is the formula of titanium oxide?
- Answer
-
\(\ce{TiO2}\)
In a simple cubic array of anions, there is one cubic hole that can be occupied by a cation for each anion in the array. In CsCl, and in other compounds with the same structure, all of the cubic holes are occupied. Half of the cubic holes are occupied in SrH2, UO2, SrCl2, and CaF2.
Different types of ionic compounds often crystallize in the same structure when the relative sizes of their ions and their stoichiometries (the two principal features that determine structure) are similar.
Unit Cells of Ionic Compounds
Many ionic compounds crystallize with cubic unit cells, and we will use these compounds to describe the general features of ionic structures. When an ionic compound is composed of cations and anions of similar size in a 1:1 ratio, it typically forms a simple cubic structure. Cesium chloride, CsCl, (Figure \(\PageIndex{14}\)) is an example of this, with Cs+ and Cl− having radii of 174 pm and 181 pm, respectively. We can think of this as chloride ions forming a simple cubic unit cell, with a cesium ion in the center; or as cesium ions forming a unit cell with a chloride ion in the center; or as simple cubic unit cells formed by Cs+ ions overlapping unit cells formed by Cl− ions. Cesium ions and chloride ions touch along the body diagonals of the unit cells. One cesium ion and one chloride ion are present per unit cell, giving the l:l stoichiometry required by the formula for cesium chloride. Note that there is no lattice point in the center of the cell, and CsCl is not a BCC structure because a cesium ion is not identical to a chloride ion.

We have said that the location of lattice points is arbitrary. This is illustrated by an alternate description of the CsCl structure in which the lattice points are located in the centers of the cesium ions. In this description, the cesium ions are located on the lattice points at the corners of the cell, and the chloride ion is located at the center of the cell. The two unit cells are different, but they describe identical structures.
When an ionic compound is composed of a 1:1 ratio of cations and anions that differ significantly in size, it typically crystallizes with an FCC unit cell, like that shown in Figure \(\PageIndex{15}\). Sodium chloride, NaCl, is an example of this, with Na+ and Cl− having radii of 102 pm and 181 pm, respectively. We can think of this as chloride ions forming an FCC cell, with sodium ions located in the octahedral holes in the middle of the cell edges and in the center of the cell. The sodium and chloride ions touch each other along the cell edges. The unit cell contains four sodium ions and four chloride ions, giving the 1:1 stoichiometry required by the formula, NaCl.

The cubic form of zinc sulfide, zinc blende, also crystallizes in an FCC unit cell, as illustrated in Figure \(\PageIndex{16}\). This structure contains sulfide ions on the lattice points of an FCC lattice. (The arrangement of sulfide ions is identical to the arrangement of chloride ions in sodium chloride.) The radius of a zinc ion is only about 40% of the radius of a sulfide ion, so these small Zn2+ ions are located in alternating tetrahedral holes, that is, in one half of the tetrahedral holes. There are four zinc ions and four sulfide ions in the unit cell, giving the empirical formula ZnS.

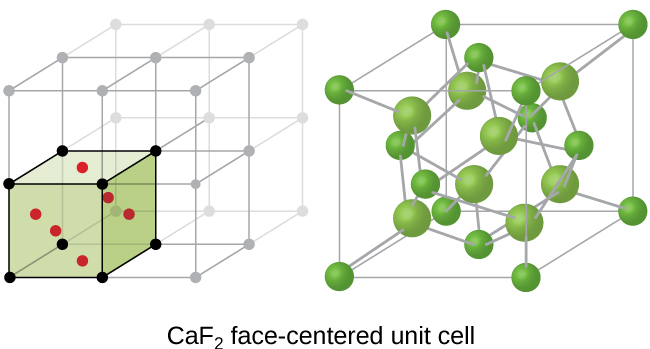
A calcium fluoride unit cell, like that shown in Figure \(\PageIndex{17}\), is also an FCC unit cell, but in this case, the cations are located on the lattice points; equivalent calcium ions are located on the lattice points of an FCC lattice. All of the tetrahedral sites in the FCC array of calcium ions are occupied by fluoride ions. There are four calcium ions and eight fluoride ions in a unit cell, giving a calcium:fluorine ratio of 1:2, as required by the chemical formula, CaF2. Close examination of Figure \(\PageIndex{17}\) will reveal a simple cubic array of fluoride ions with calcium ions in one half of the cubic holes. The structure cannot be described in terms of a space lattice of points on the fluoride ions because the fluoride ions do not all have identical environments. The orientation of the four calcium ions about the fluoride ions differs.
Calculation of Ionic Radii
If we know the edge length of a unit cell of an ionic compound and the position of the ions in the cell, we can calculate ionic radii for the ions in the compound if we make assumptions about individual ionic shapes and contacts.
Example \(\PageIndex{5}\): Calculation of Ionic Radii
The edge length of the unit cell of LiCl (NaCl-like structure, FCC) is 0.514 nm or 5.14 Å. Assuming that the lithium ion is small enough so that the chloride ions are in contact, calculate the ionic radius for the chloride ion. Note: The length unit angstrom, Å, is often used to represent atomic-scale dimensions and is equivalent to 10−10 m.
Solution
On the face of a LiCl unit cell, chloride ions contact each other across the diagonal of the face:
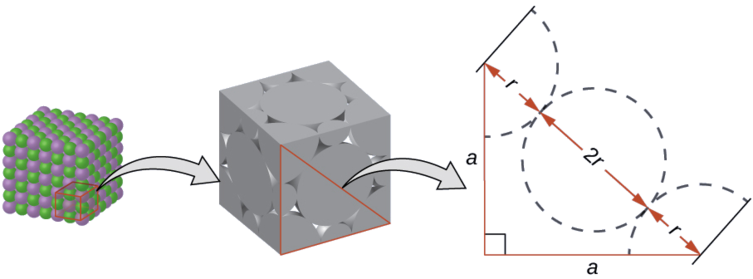
Drawing a right triangle on the face of the unit cell, we see that the length of the diagonal is equal to four chloride radii (one radius from each corner chloride and one diameter—which equals two radii—from the chloride ion in the center of the face), so \(d = 4r\). From the Pythagorean theorem, we have:
\[a^2+a^2=d^2 \nonumber \]
which yields:
\[\mathrm{(0.514\:nm)^2+(0.514\:nm)^2}=(4r)^2=16r^2 \nonumber \]
Solving this gives:
\[r=\mathrm{\sqrt{\dfrac{(0.514\:nm)^2+(0.514\:nm)^2}{16}}=0.182\: nm\:(1.82\: Å)\:for\: a\: Cl^−\: radius.} \nonumber \]
Exercise \(\PageIndex{6}\)
The edge length of the unit cell of KCl (NaCl-like structure, FCC) is 6.28 Å. Assuming anion-cation contact along the cell edge, calculate the radius of the potassium ion. The radius of the chloride ion is 1.82 Å.
- Answer
-
The radius of the potassium ion is 1.33 Å.
It is important to realize that values for ionic radii calculated from the edge lengths of unit cells depend on numerous assumptions, such as a perfect spherical shape for ions, which are approximations at best. Hence, such calculated values are themselves approximate and comparisons cannot be pushed too far. Nevertheless, this method has proved useful for calculating ionic radii from experimental measurements such as X-ray crystallographic determinations.
X-Ray Crystallography
The size of the unit cell and the arrangement of atoms in a crystal may be determined from measurements of the diffraction of X-rays by the crystal, termed X-ray crystallography. Diffraction is the change in the direction of travel experienced by an electromagnetic wave when it encounters a physical barrier whose dimensions are comparable to those of the wavelength of the light. X-rays are electromagnetic radiation with wavelengths about as long as the distance between neighboring atoms in crystals (on the order of a few Å).
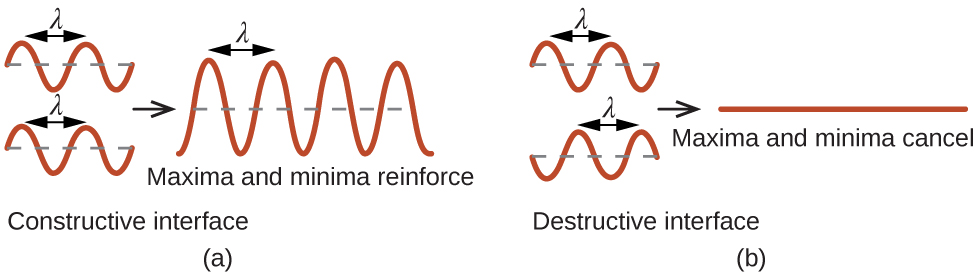
When a beam of monochromatic X-rays strikes a crystal, its rays are scattered in all directions by the atoms within the crystal. When scattered waves traveling in the same direction encounter one another, they undergo interference, a process by which the waves combine to yield either an increase or a decrease in amplitude (intensity) depending upon the extent to which the combining waves’ maxima are separated (Figure \(\PageIndex{18}\)).
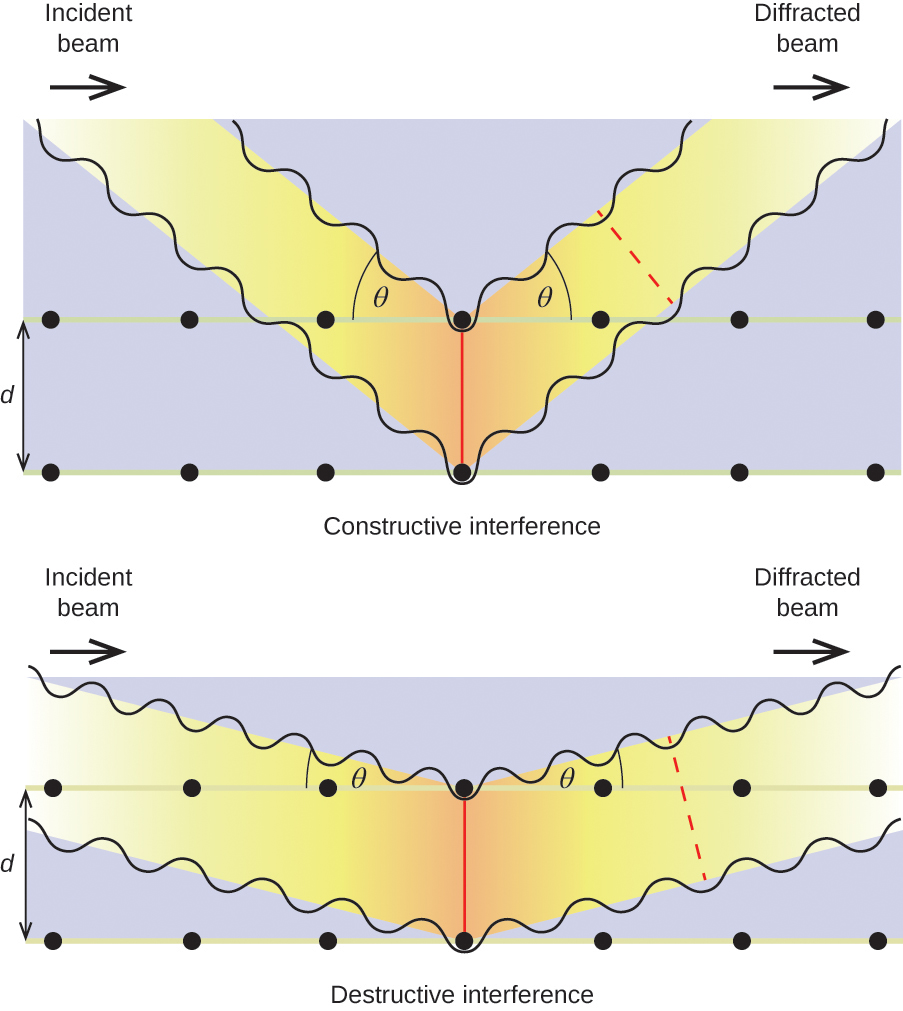
When X-rays of a certain wavelength, λ, are scattered by atoms in adjacent crystal planes separated by a distance, d, they may undergo constructive interference when the difference between the distances traveled by the two waves prior to their combination is an integer factor, n, of the wavelength. This condition is satisfied when the angle of the diffracted beam, θ, is related to the wavelength and interatomic distance by the equation:
\[nλ=2d\sin \theta \label{Eq1} \]
This relation is known as the Bragg equation in honor of W. H. Bragg, the English physicist who first explained this phenomenon. Figure \(\PageIndex{18}\) illustrates two examples of diffracted waves from the same two crystal planes. The figure on the left depicts waves diffracted at the Bragg angle, resulting in constructive interference, while that on the right shows diffraction and a different angle that does not satisfy the Bragg condition, resulting in destructive interference.
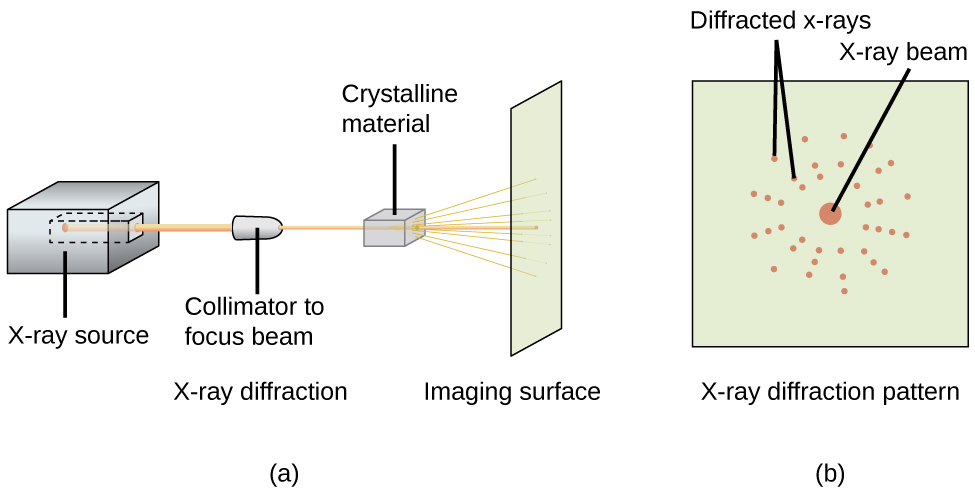
An X-ray diffractometer, such as the one illustrated in Figure \(\PageIndex{20}\), may be used to measure the angles at which X-rays are diffracted when interacting with a crystal as described earlier. From such measurements, the Bragg equation may be used to compute distances between atoms as demonstrated in the following example exercise.
Example \(\PageIndex{6}\): Using the Bragg Equation
In a diffractometer, X-rays with a wavelength of 0.1315 nm were used to produce a diffraction pattern for copper. The first order diffraction (n = 1) occurred at an angle θ = 25.25°. Determine the spacing between the diffracting planes in copper.
Solution
The distance between the planes is found by solving the Bragg equation (Equation \(\ref{Eq1}\)) for d.
This gives
\[d=\dfrac{nλ}{2\sinθ}=\mathrm{\dfrac{1(0.1315\:nm)}{2\sin(25.25°)}=0.154\: nm}\nonumber \]
Exercise \(\PageIndex{6}\)
A crystal with spacing between planes equal to 0.394 nm diffracts X-rays with a wavelength of 0.147 nm. What is the angle for the first order diffraction?
- Answer
-
21.9°
X-ray Crystallographer Rosalind Franklin
The discovery of the structure of DNA in 1953 by Francis Crick and James Watson is one of the great achievements in the history of science. They were awarded the 1962 Nobel Prize in Physiology or Medicine, along with Maurice Wilkins, who provided experimental proof of DNA’s structure. British chemist Rosalind Franklin made invaluable contributions to this monumental achievement through her work in measuring X-ray diffraction images of DNA. Early in her career, Franklin’s research on the structure of coals proved helpful to the British war effort. After shifting her focus to biological systems in the early 1950s, Franklin and doctoral student Raymond Gosling discovered that DNA consists of two forms: a long, thin fiber formed when wet (type “B”) and a short, wide fiber formed when dried (type “A”). Her X-ray diffraction images of DNA provided the crucial information that allowed Watson and Crick to confirm that DNA forms a double helix, and to determine details of its size and structure. Franklin also conducted pioneering research on viruses and the RNA that contains their genetic information, uncovering new information that radically changed the body of knowledge in the field. After developing ovarian cancer, Franklin continued to work until her death in 1958 at age 37. Among many posthumous recognitions of her work, the Chicago Medical School of Finch University of Health Sciences changed its name to the Rosalind Franklin University of Medicine and Science in 2004, and adopted an image of her famous X-ray diffraction image of DNA as its official university logo.

Key Concepts and Summary
The structures of crystalline metals and simple ionic compounds can be described in terms of packing of spheres. Metal atoms can pack in hexagonal closest-packed structures, cubic closest-packed structures, body-centered structures, and simple cubic structures. The anions in simple ionic structures commonly adopt one of these structures, and the cations occupy the spaces remaining between the anions. Small cations usually occupy tetrahedral holes in a closest-packed array of anions. Larger cations usually occupy octahedral holes. Still larger cations can occupy cubic holes in a simple cubic array of anions. The structure of a solid can be described by indicating the size and shape of a unit cell and the contents of the cell. The type of structure and dimensions of the unit cell can be determined by X-ray diffraction measurements.
Glossary
- body-centered cubic (BCC) solid
- crystalline structure that has a cubic unit cell with lattice points at the corners and in the center of the cell
- body-centered cubic unit cell
- simplest repeating unit of a body-centered cubic crystal; it is a cube containing lattice points at each corner and in the center of the cube
- Bragg equation
- equation that relates the angles at which X-rays are diffracted by the atoms within a crystal
- coordination number
- number of atoms closest to any given atom in a crystal or to the central metal atom in a complex
- cubic closest packing (CCP)
- crystalline structure in which planes of closely packed atoms or ions are stacked as a series of three alternating layers of different relative orientations (ABC)
- diffraction
- redirection of electromagnetic radiation that occurs when it encounters a physical barrier of appropriate dimensions
- face-centered cubic (FCC) solid
- crystalline structure consisting of a cubic unit cell with lattice points on the corners and in the center of each face
- face-centered cubic unit cell
- simplest repeating unit of a face-centered cubic crystal; it is a cube containing lattice points at each corner and in the center of each face
- hexagonal closest packing (HCP)
- crystalline structure in which close packed layers of atoms or ions are stacked as a series of two alternating layers of different relative orientations (AB)
- hole
- (also, interstice) space between atoms within a crystal
- isomorphous
- possessing the same crystalline structure
- octahedral hole
- open space in a crystal at the center of six particles located at the corners of an octahedron
- simple cubic unit cell
- (also, primitive cubic unit cell) unit cell in the simple cubic structure
- simple cubic structure
- crystalline structure with a cubic unit cell with lattice points only at the corners
- space lattice
- all points within a crystal that have identical environments
- tetrahedral hole
- tetrahedral space formed by four atoms or ions in a crystal
- unit cell
- smallest portion of a space lattice that is repeated in three dimensions to form the entire lattice
- X-ray crystallography
- experimental technique for determining distances between atoms in a crystal by measuring the angles at which X-rays are diffracted when passing through the crystal
Paul Flowers (University of North Carolina - Pembroke), Klaus Theopold (University of Delaware) and Richard Langley (Stephen F. Austin State University) with contributing authors. Textbook content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at http://cnx.org/contents/85abf193-2bd...a7ac8df6@9.110).


