Myoglobin
- Page ID
- 98116
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Introduction to Myoglobin: O2 storage in muscle cells
The respiratory system is an organ system in the body that functions in gas exchange with the environment. Exchange of gases like carbon dioxide (CO2) and dioxygen (O2) are essential for sustaining life forms. O2 is necessary in aerobic metabolism for oxidative phosphorylation (synthesis of ATP) at the electron transport chain (ETC).2 ATP is the energy source needed for muscular contraction in mammals. ATP synthesis requires oxygen as an electron acceptor in the ETC, therefore oxygen must be readily available for use in metabolically active muscles. Since muscles need large quantities of O2, it is transported by proteins in the blood and stored in muscle tissue. One of these proteins is myoglobin.
Myoglobin is a hemoprotein found in the skeletal muscle of mammals that functions in oxygen storage and diffusion.1 A hemoprotein is a protein that contains a heme prosthetic group. The heme in myoglobin can reversibly bind a O2 molecule to regulate the transportation of O2 from red blood cells to mitochondria when skeletal muscles are metabolically active.1
Structure of Myoglobin
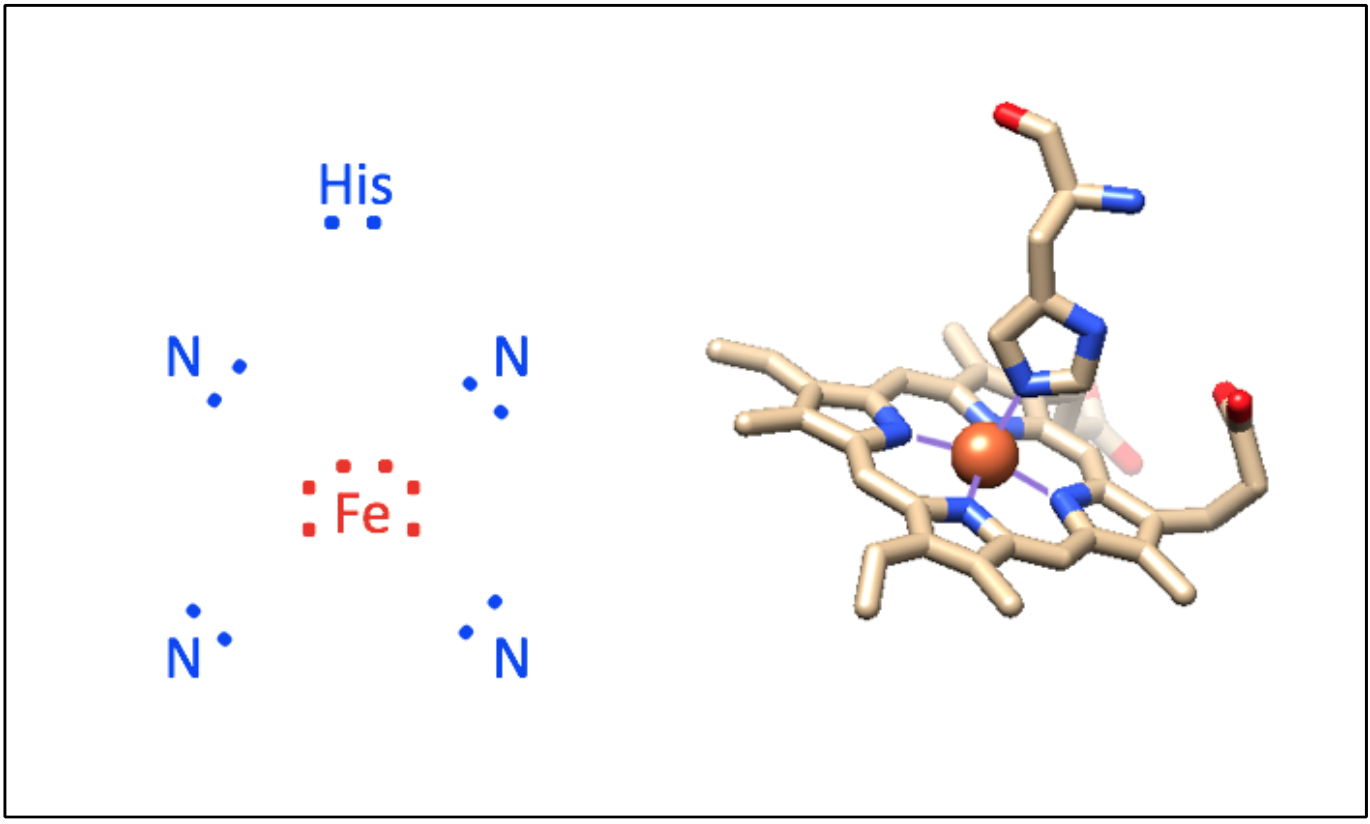
The structure of myoglobin (Figure \(\PageIndex{1}\)) is similar to the structure of one of the \(\beta\) subunits of hemoglobin. Myoglobin and hemoglobin are both part of the globin family; a family of heme-containing globular polypeptides with eight \(\alpha\)-helices in their protein fold. Myoglobin contains only one subunit of globin, while hemoglobin has four subunits.
The iron (Fe)-containing heme group allows myoglobin to reversibly bind to O2 (Figure \(\PageIndex{1}\)). Heme is a large, aromatic porphyrin ring with four pyrrole nitrogens bound to a ferrous (Fe(II)) ion at the center (Figure \(\PageIndex{1}C\)).2,3 The nitrogens from the porphyrin ring and a Histidine imidazole serve as igands for the Fe(II) metal center. The heme Fe is bound to the myoglobin polypeptide through the proximal histidine residue.2 The iron ion has six coordination sites: four equitorial sites are occupied by pyrole nitrogens of heme, and one axial site is occupied by a proximal histidine residue.2 The remaining axial coordination site is available for binding a O2 molecule (Figure \(\PageIndex{1}A-C\)).3
Applying Principles of Inorganic Chemistry
The following is a discussion of how properties of myoglobin can be explained by principles of inorganic chemistry.
A) THERMODYNAMICS and KINETICS of Fe BINDING to HEME
Fe(II) bound within a heme group is thermodynamically stable and relatively inert.
Ligand Field Theory (LFT)
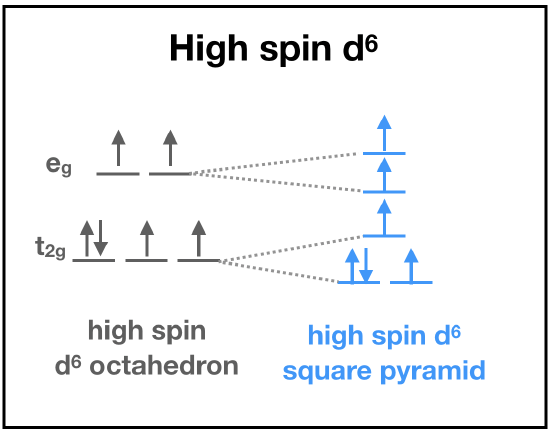 First, let's predict the electronic structure of Fe(II) bound to heme. Fe(II) is a first-row transition metal with relatively low charge, and so LFT predicts a high-spin electronic configuration. But, we still need to consider the ligand set. The the porphoryn ring and the imidazole are \(\sigma\)-donor and \(\pi\)-accepting ligands, and thus LFT predicts the set to contribute to a strong field that increases \(\delta\). When we have a first-row, +2 transition metal with a set of strong field ligands, it is difficult to predict what the actual electronic structure will be without more information. This is where actual data becomes important for predicting electronic structure. Magnetic measurement of the Fe(II) center is consistent with four unpaired electrons. This can only be explained by a high-spin d6 Fe(II).
First, let's predict the electronic structure of Fe(II) bound to heme. Fe(II) is a first-row transition metal with relatively low charge, and so LFT predicts a high-spin electronic configuration. But, we still need to consider the ligand set. The the porphoryn ring and the imidazole are \(\sigma\)-donor and \(\pi\)-accepting ligands, and thus LFT predicts the set to contribute to a strong field that increases \(\delta\). When we have a first-row, +2 transition metal with a set of strong field ligands, it is difficult to predict what the actual electronic structure will be without more information. This is where actual data becomes important for predicting electronic structure. Magnetic measurement of the Fe(II) center is consistent with four unpaired electrons. This can only be explained by a high-spin d6 Fe(II).
We can use the "ideal" case of octahedral geometry to predict stability and kinetics:
♦ LFT (using Taube's rules) predicts that high-spin d6 metal ions are kinetically labile because the higher-energy set of orbitals (eg in octahedron) are occupied by electrons.
♦ Calculation of ligand field stabilization energy (LFSE) gives approximately -0.4 \(\delta_o\) in the case of an octahedron.
LFT only gives us part of the story, and alone it is inconclusive and misleading in this case. We should certainly consider other factors that influence thermodynamics and kinetics.
The Chelate and Macrocycle Effect
The chelate effect refers to the fact that multidentate ligands have greater stability compared to an analogous set of monodentate ligands. The macrocycle effect offers even greater stability when the donor atoms of a multidentate ligand are pre-arranged in an orientation that is ideal for metal binding. The chelate and macrocycle effect each increase thermodynamic stability. Additionally, chelates and macrocycles produce complexes that are more kinetically inert than the monodentate ligands.
Heme is a tetradentate ligand made up of a large, aromatic porphyrin ring with four pyrrole nitrogens and a ferrous, or Fe (II), ion at the center. The 4 nitrogens from the porphyrin ring of heme allow it to serve as a tetradentate chelator for the Fe(II) ion, and since they are in a ring, it is also influenced by the macrocycle effect. Further, if you consider the heme-protein as a unit, with heme held in place by intermolecular forces between the porphoryn ring and the polypeptide, the entire heme-protein unit might be considered a pentadentate chelator, with the nitrogen from the imidazole of the proximal histidine residue as the fifth "bite". The chelate and macrocycle effects would allow us to predict that Fe is tightly bound in the heme group, and that once bound, removal of the Fe would be extremely slow (inert). The chelate effect can explain why Fe in heme is stable and inert despite what would be predicted based on LFT.
Hard-Soft Acid-Base (HSAB)
HSAB theory classifies metals and ligands into hard, soft, and borderline categories based on their charge density and the groups character of metal-ligand bonding (covalent bonding vs. electrostatic interactions). The general trend for acid-base interactions is “like prefers like”. This means that hard acids prefer to interact with hard bases, soft acids prefer soft bases, and borderline acids prefer borderline bases. All metal-ligand interactions are acid-base interactions: the metal is a Lewis acid, while the ligand is a Lewis Base. Fe(II) is classified as a borderline acid. Fe(II) is held in place by four pyrrole nitrogens from the porphyrin aromatic ring and one nitrogen from the imidazole histidine residue. Nitrogen is usually categorized as a hard base, however N is classified as a borderline bases when it is part of a polarizable aromatic system, like that of a porphyrin ring or an imidazole ring. The nitrogens that bind to Fe in myoglobin are borderline bases, and thus are a good match to interact strongly with the borderline Fe(II) ion. HSAB theory would predict a stable myoglobin-Fe interaction.
Electrostatic Attraction
Coulomb's law can be used to predict thermodynamic stability and relative kinetic rates of metal-ligand association and dissociation reactions based on electrostatic attraction. According to Coulomb, opposite charges experience electrostatic attraction. The greater the magnitude of opposite charge, the stronger the attraction will be. When metal-ligand pairs have strong electrostatic attraction, they are more thermodynamically stable, and the ligands dissociate from the metal more slowly (more inert).
The Fe(II) ion is held within heme in part due to electrostatic attraction. The Fe(II) has a positive two (+2) charged that, according to Coulomb's Law, is attracted to the negative charge density of the pyrole nitrogen atoms. Two of the heme nitrogens must be deprotonated upon Fe-binding, and so the heme formally has a negative two (-2) charge. The attraction between the (+2) Fe and the (-2) heme is expected to yield a more stable and kinetically inert complex than if the atoms involved had less ionic charge.
B) REVERSIBLE BINDING TO DIOXYGEN
Now let’s move on to the function of myoglobin: oxygen storage. Myoglobin can reversibly bind a dioxygen molecule to regulate the transportation of oxygen from red blood cells to mitochondria when skeletal muscles are metabolically active. This binding occurs at the iron center of the heme group.
The 18-electron rule
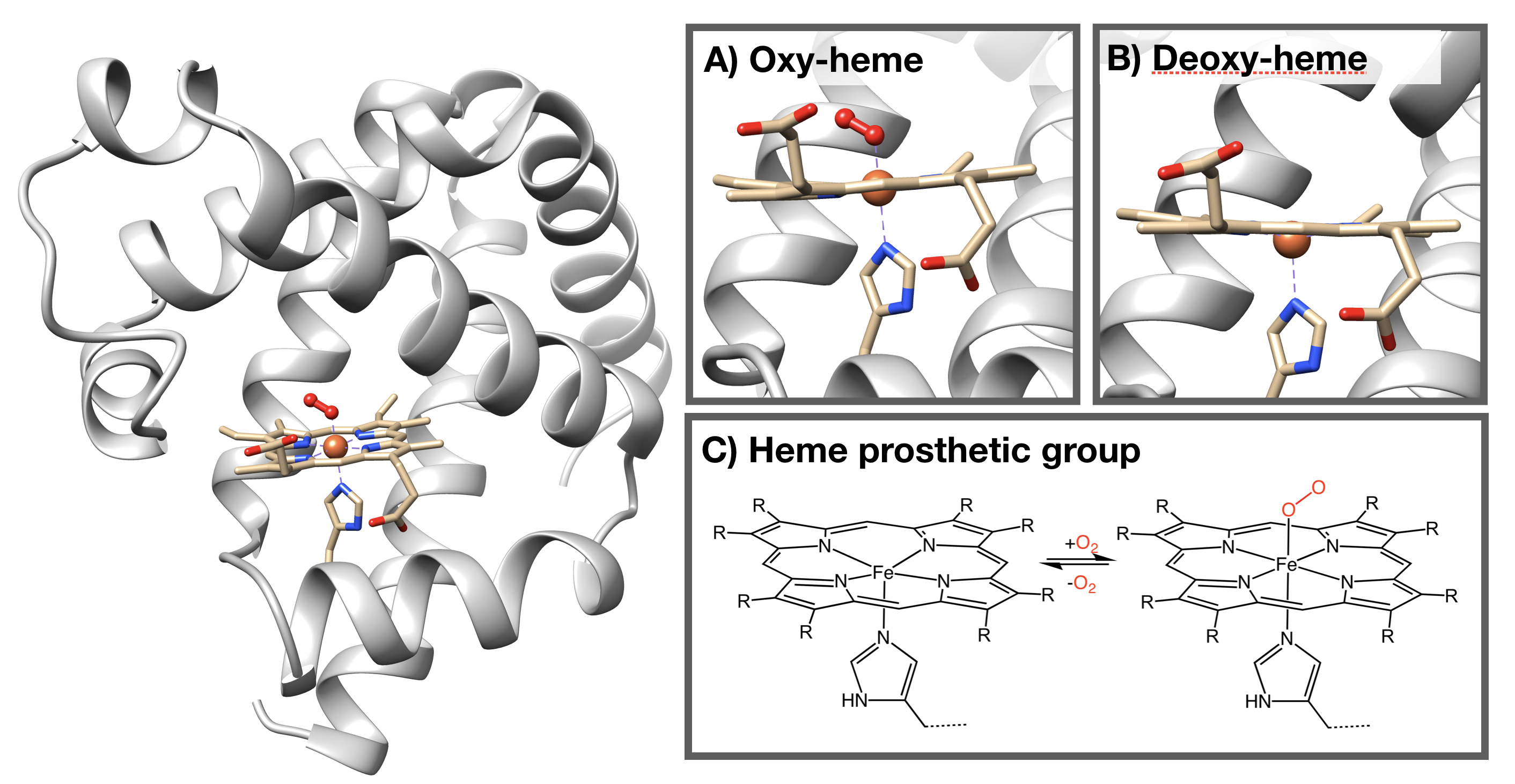
Although the 18-electron rule was a rule developed to predict steps in the mechanism of inorganic catalysis, we can apply it here to explain the O2-binding behavior of myoglobin. In deoxymyoglobin, the total valence electron count around Fe is 16 electrons (See Fig. \(\PageIndex{2}\), 10 electrons from ligands plus 6 electrons from Fe(II)). Under the 18-electron rule, a predictable step for a 16-electron species is ligand addition. The binding of O2 to Fe(II) is a ligand addition reaction. Once O2 binds to the Fe(II) in myoglobin, the new valence electron count around Fe is 18 electron. A predictable step for an 18-electron species is a ligand dissociation reaction, as is the reaction of O2 dissociation from the Fe center. The binding and dissociation of O2 makes sense based on the 18-electron rule.
Figure \(\PageIndex{2}\). Counting electrons. The electron count of deoxygenated heme Fe is 16 electrons. A total of 10 electrons are donated from the ligands (8 from pyrrole nitrogens of the porphyrin ring and 2 from the imidaziole nitrogen of the proximal histidine); 6 electrons are present from the 6 d electrons of Fe(II). Thus, the deoxy-heme complex is available for another ligand to bind; this case in the form of oxygen. The image was created using PDB code 1a6n and UCSF Chimera.
C) Fe OXIDATION STATE AND ELECTRONIC STRUCTURE
The oxidation state of Fe in oxy-myoglobin is a highly debated topic because data is inconclusive and seemingly contradictory. Data from infrared (IR) spectroscopy and magnetic measurements have lead scientists to propose two different modes of oxygen binding to the iron ion. In one model (Fig. \(\PageIndex{3}\) left), Fe(II) simply binds to O2. A second model predicts that electrons are transfered from the Fe center to the dioxygen molecule to create Fe(III) bound to superoxide (Fig. \(\PageIndex{3}\) right).5
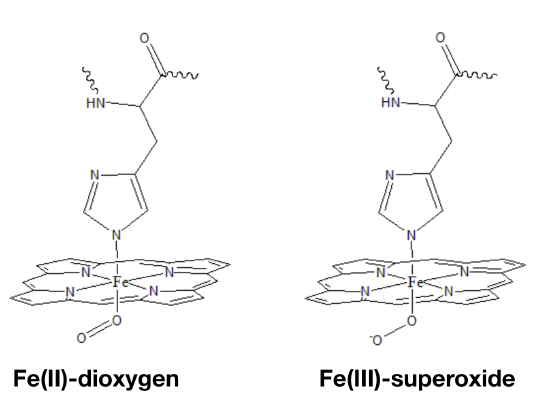
Evidence for Fe(III)
Data from IR spectroscopy has lead to the prediction that the Fe center in myoglobin is Fe(III). IR spectroscopy can measure vibrational properties and bond length of dioxygen species; specifically, the O─O bond length can be measured by measuring the vibrational frequency of the O─O bond. IR measurements tell us that oxygenated myoglobin has an O─O bond vibration frequency of ~1105cm-1. This frequency is much closer to the O─O bond vibration frequency of superoxide (~1097cm-1) than that of an O2 molecule (~1580cm-1). This data suggests that the dioxygen bound to myoglobin has a similar bond length to that of superoxide. If the dioxygen bound to oxy-myoglobin is more like superoxide than the original O2 molecule, then it would follow that the Fe center is in the Fe(III) oxidation state.
There are some problems with the conclusion that Fe in oxygenated myoglobin is Fe(III). One problem is that [under construction]
Evidence for Fe(II)
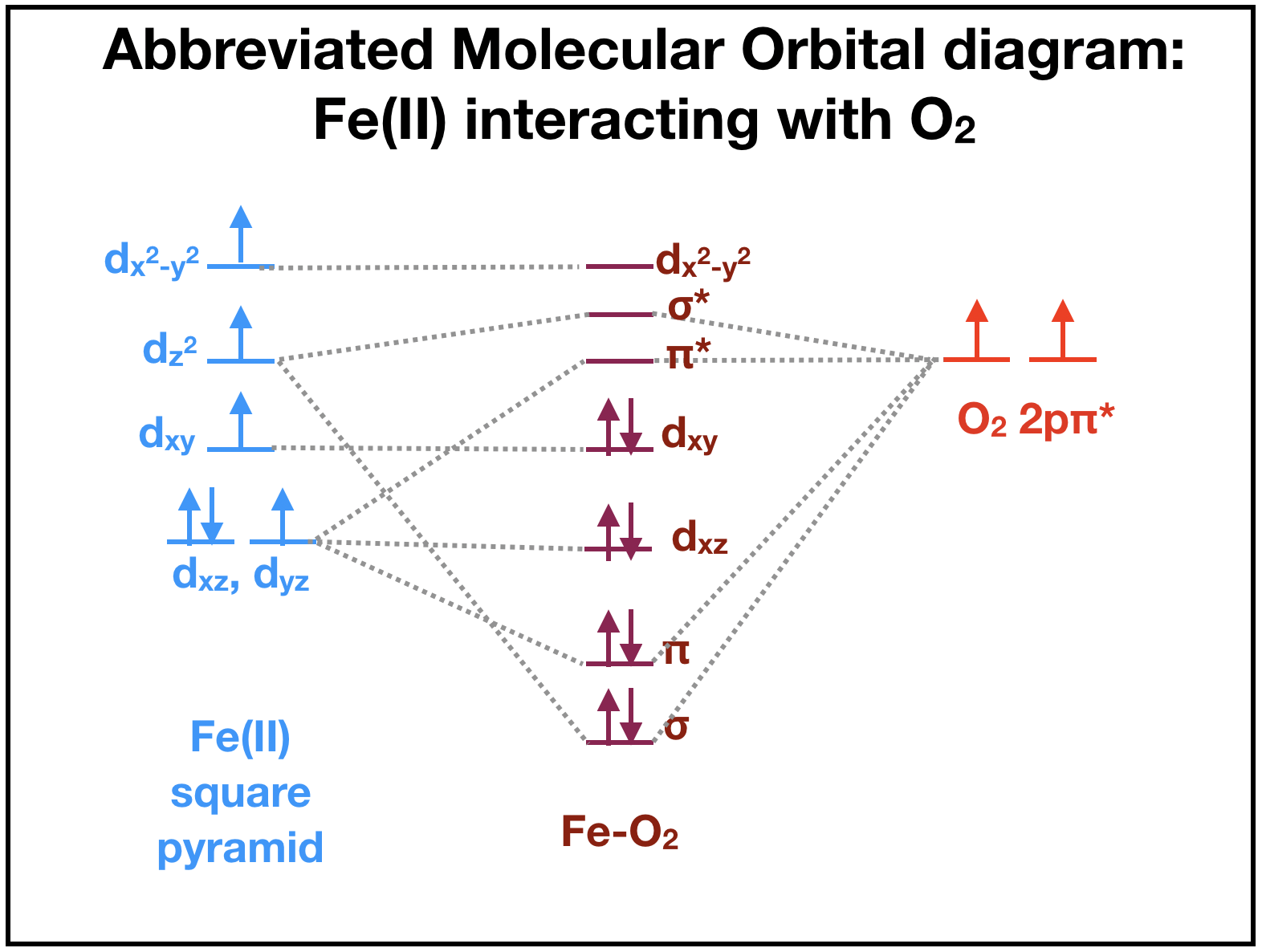
This section is under construction. Magnetic measurements of Fe(II) lead to assumptions that oxygen binding to Fe(II) is preferred over binding to Fe(III). The ligand field theory suggests that deoxygenated myoglobin with a high-spin Fe(II) ion is paramagnetic because there are four unpaired electrons (Fig. \(\PageIndex{4}\), left). When oxygen is available to bind, there are \(\pi\)* orbitals containing two unpaired electrons ((Fig. \(\PageIndex{4}\), right) that can interact with Fe(II). The resulting iron-oxygen complex of heme becomes diamagnetic as all electrons are paired in the resulting molecular oritals (Fig. \(\PageIndex{4}\), middle). This suggests that oxygen binding to the Fe(II) ion is favored because the complex becomes diamagnetic. (is this right?)
Although many debate whether the iron, after binding to oxygen, remains iron (II) or becomes iron (III), it is difficult to assign an oxidation state to the bound iron or the oxygen. The actual molecular orbitals that result from the iron-oxygen interaction have both iron and O2 character. It is therefore not quite correct to focus on the electrons "belong" to Fe or dioxygen. The two extremes, where one is that Fe becomes an iron superoxide by donating an electron from iron to the oxygen, and the other that Fe becomes an iron oxide by sharing the electrons are probably both incorrect. The molecular orbitals contain characteristics of both iron superoxide and iron oxide.
Absorption of visible light
Additionally, the electronic absorption of the heme prosthetic group is charge transfer, indicating that the binding of oxygen forms a superoxide, rather than an iron oxide. Charge transfer transitions occur between metal ions and their ligands. In the case of myoglobin, the O2 molecule that binds to the metal iron ion center is a pi donor ligand, characterizing the charge transfer as ligand to metal. The pi* orbital of the O2 molecule overlaps with the metal ion orbitals to create the bond with Fe(III). The heme prosthetic group in myoglobin is absorbed at ~540-580 nm in a simple aqueous solution, meaning it reflects the color red, with an extinction coefficient around 1800M-1cm-1.7,8 This indicates that the interaction between the electrons of ligands and metals is ligand to metal charge transfer.
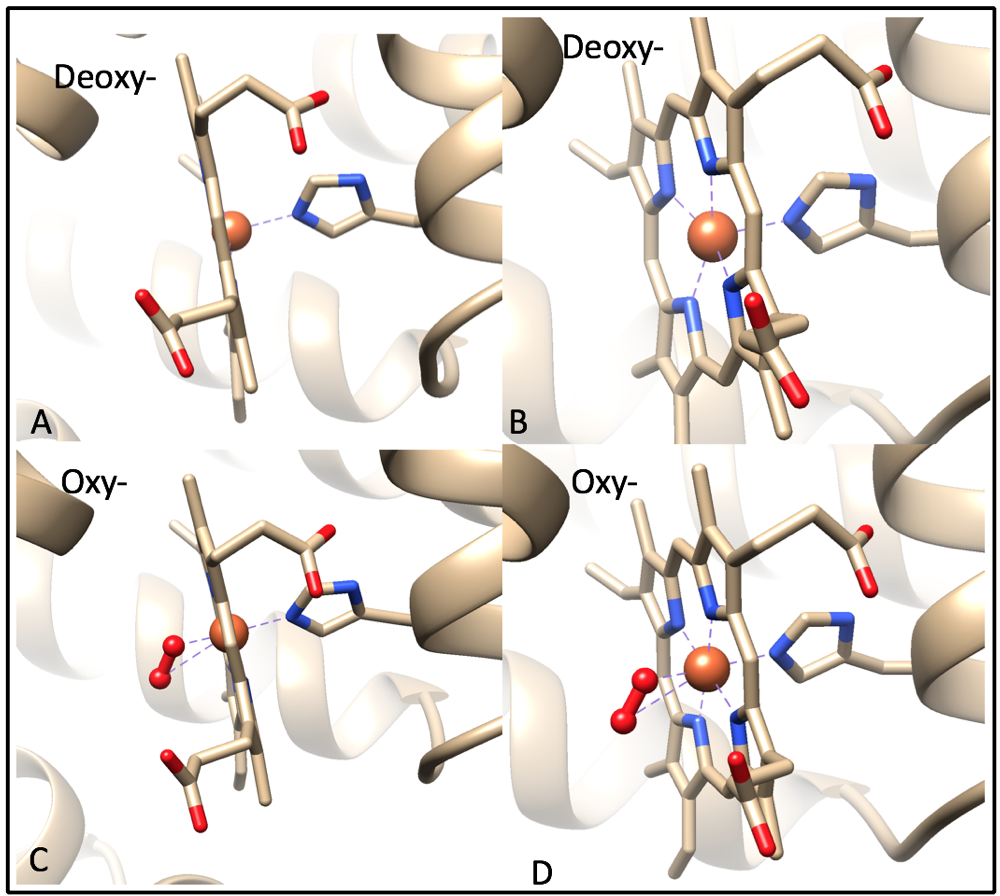
For the purpose of this discussion, I will assume that oxy-myoglobin contains an Fe(II) metal center. When oxygen is not bound to the iron ion, the Fe(II) is high spin and lies 0.4 Å outside of heme, making it nonplanar (Fig. 8A).9 This is because the valence electrons from the iron ion and valence electrons from the histidine create electron densities repel each other, pushing the two clouds apart. When oxygen is bound to the iron ion, the oxygen molecule hydrogen bonding to the imidazole nitrogen of the proximal histidine residue.3,9 The binding of the O2 molecule changes Fe(II) from high spin to low spin because oxygen is a strong field pi-accepting ligand. There are no d-electrons in the antibonding orbitals of Fe(II), causing it to shrink and shift into the plane of the ring (Fig. 8C).9
The affinity of Fe(II) as the metal center in this complex can be explained by HSAB (Hard-Soft Acid-Base) theory. HSAB theory classifies metals and ligands into different categories based on their character, including charge density and metal-ligand complex interactions such as covalent bonding and electrostatic interactions.4 Fe(II) is categorized as a borderline acid due to its charge to ionic radius ratio and the electrostatic interactions it partakes in. Fe(II) is held in place by four pyrrole nitrogens from the porphyrin aromatic ring and one nitrogen from the imidazole histidine residue. Nitrogen is typically categorized as a hard base, however due to the high polarizability of the porphyrin ring and imidazole histidine in heme, the nitrogens are considered borderline. The general trend for interactions between metals and ligands is “like prefers like”. This means that hard acids prefer to bind with hard bases, soft acids prefer to bind with soft bases, and borderline acids prefer to bind with borderline bases. This generalization is explains how the structure of the heme group in myoglobin tightly holds Fe(II) at its center.
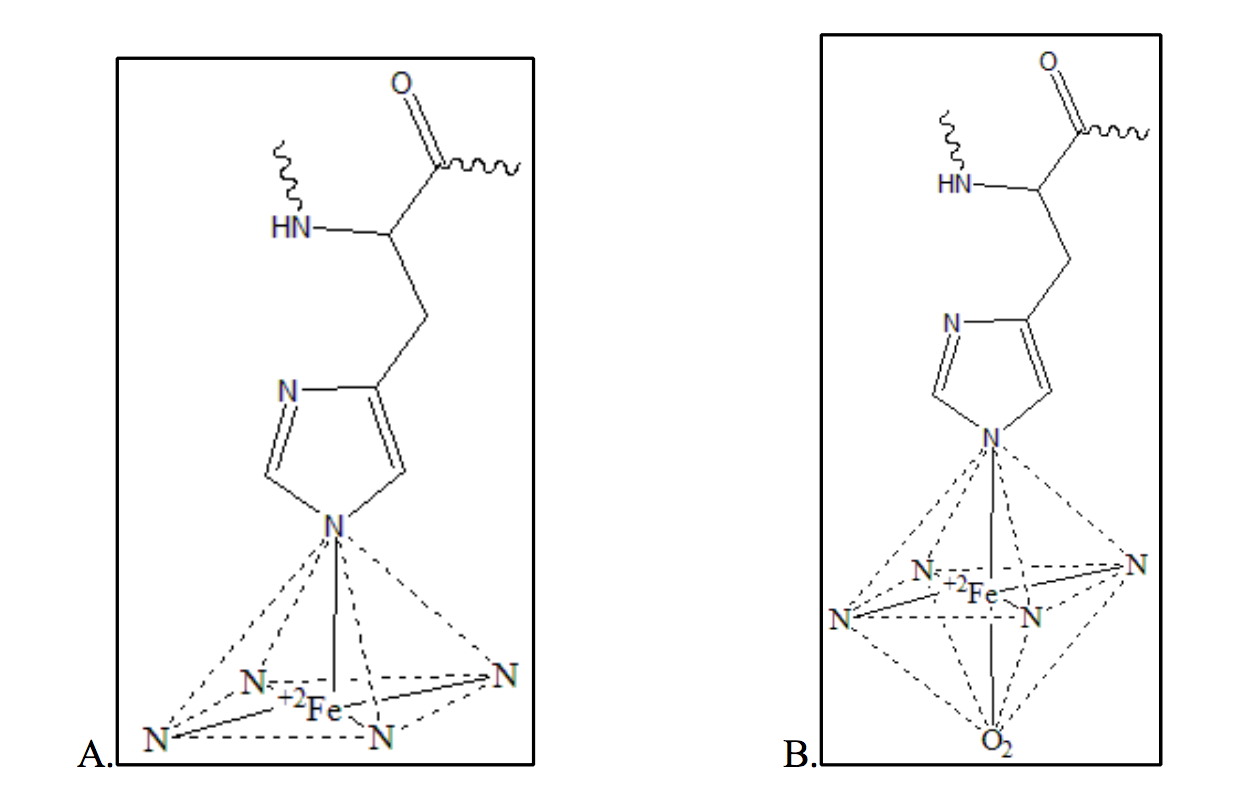
The metal center in the heme prosthetic group of myoglobin is a ferrous (Fe(II)) ion (Fig. 9). Because deoxymyoglobin and oxymyoglobin contain 5 and 6 occupied coordination sites around the iron ion respectively, the metal centers maintain two different geometries. When the iron ion is deoxygenated, the heme group maintains a square pyramidal geometry (Figure 9A). This means only five of the six coordination sites are occupied. When the iron ion is oxygenated and all six coordinate sites are occupied symmetrically, the heme group to maintains octahedral geometry (Figure 9B).
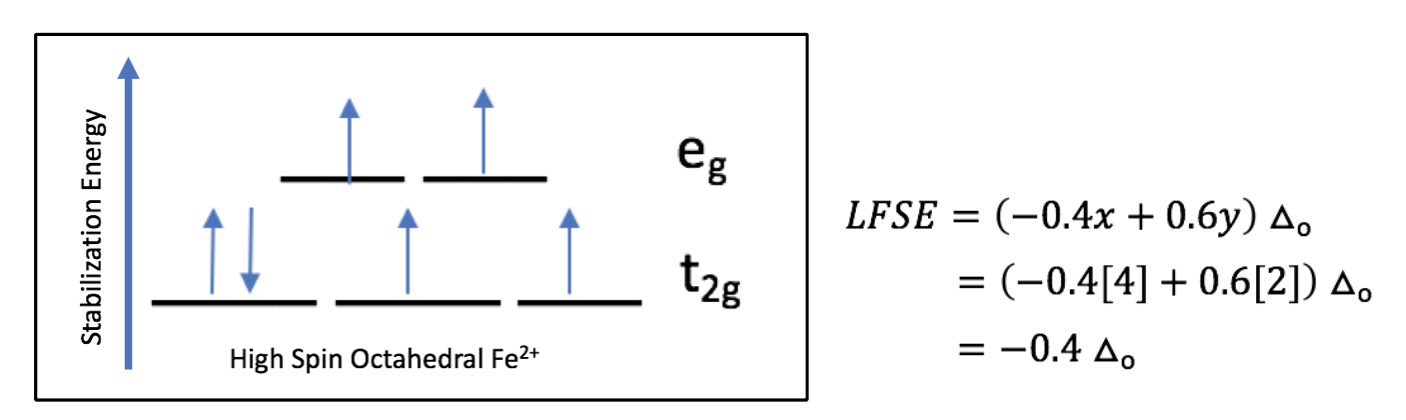
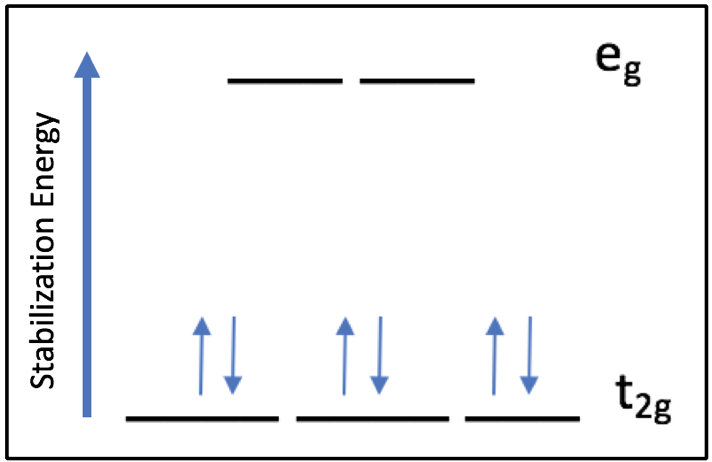
Based on the Ligand Field Stabilization Energy, the binding of oxygen to the Fe(II) ion is favorable because a high-spin octahedral Fe(II) has an LFSE of -0.4, making it labile and willing to bind another ligand (Fig. 10). When oxygen binds, the complex becomes octahedral in geometry and thus maintains a low-spin electronic arrangement. The O2 molecule is a pi accepting atom which favors low spin, and the porphyrin ring of heme is low spin. Despite the high spin nature of the Fe(II) ion in heme, the interactions between iron and the porphyrin ring and oxygen create an overall low spin for the system. The low spin configuration would suggest that there are a low amount of unpaired electrons, which is in agreement with the LFSE diagram of an octahedral low spin Fe(II) ion (Fig. 11).
One human disease that is associated with myoglobin is rhabdomyolysis. This disease is the result of muscular tissues breaking down, which releases contents of muscle cells into circulatory system.10 One of these contents is myoglobin, which is the protein that stores oxygen within muscle tissues. When large amounts of myoglobin are released into the blood, myoglobin gets filtered by the kidneys. The kidneys cannot support this filtration, and thus kidney cells are damaged. This repetitive damage ultimately results in renal dysfunction.10
Sources
- Ordway, G. A. Journal of Experimental Biology 2004, 207(20), 3441–3446.
- Ahern, K.; Rajagopal, I.; Tan, T. Biochemistry Free For All; Creative Commons, 2017; Vol. 1.2.
- Casiday, R.; Frey, R. Hemoglobin and the Heme Group: Metal Complexes in the Blood for Oxygen Transport Inorganic Synthesis Experiment
- Penn State University. In Chem 324: Bio-Inorganic Chemistry.
- Lippard, S.J., Berg, J.M. Principles of Bioinorganic Chemistry. University Science Books. 1994. 284-289.
- Atkins, Overton, Rourke, Weller, Armstrong. Shriver and Atkins’ Inorganic Chemistry. Oxford University Press. 2010. 738-79.
- Richards, M. Antioxidants and Redox Signaling 2013. 2342-2351.
- Mazumdra, S., Medhi, O.K., Mitra, S. American Chemical Society. 1990. 700-705.
- Shriver, D., Atkins, P. Inorganic Chemistry, 5th ed.; W.H. Freeman and Company: New York, 2009; 739.
- Vanholder, R., Sever, M.S., Erek, E., Lameire, N. 2000. Rhabdomyolysis. Journal of the American Society of Nephrology 11:1553-1561
Contributed By:
This work was originally written by Lydia Lorenc, Spring 2018: Lydia is currently (as of 2018) a junior chemistry major at Saint Mary's College in Notre Dame, IN.
This work was originally edited by Dr. Kathryn Haas, Assistant Professor and Madison Sendzik, Teaching and Research Assistant of Saint Mary's College.