NDM-1: Metallobetalactamases (MBLs) and Antibiotic Resistance
- Page ID
- 97959
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)β-lactam Antibiotics
Beta-lactam antibiotics are used to treat a wide range of bacterial infections and occur in several classes including penicillins, cephalosporins, monobactams, and carbapenems.1 They are characterized by a four-membered heterocyclic ring (see Figure 1). The nitrogen in this ring binds to penicillin-binding proteins (PBPs) in the cell membrane of bacteria. These PBPs crosslink within the cell membrane and the beta-lactam interferes with the crosslinking process, disrupting the cell’s integrity and causing the bacteria’s death.1
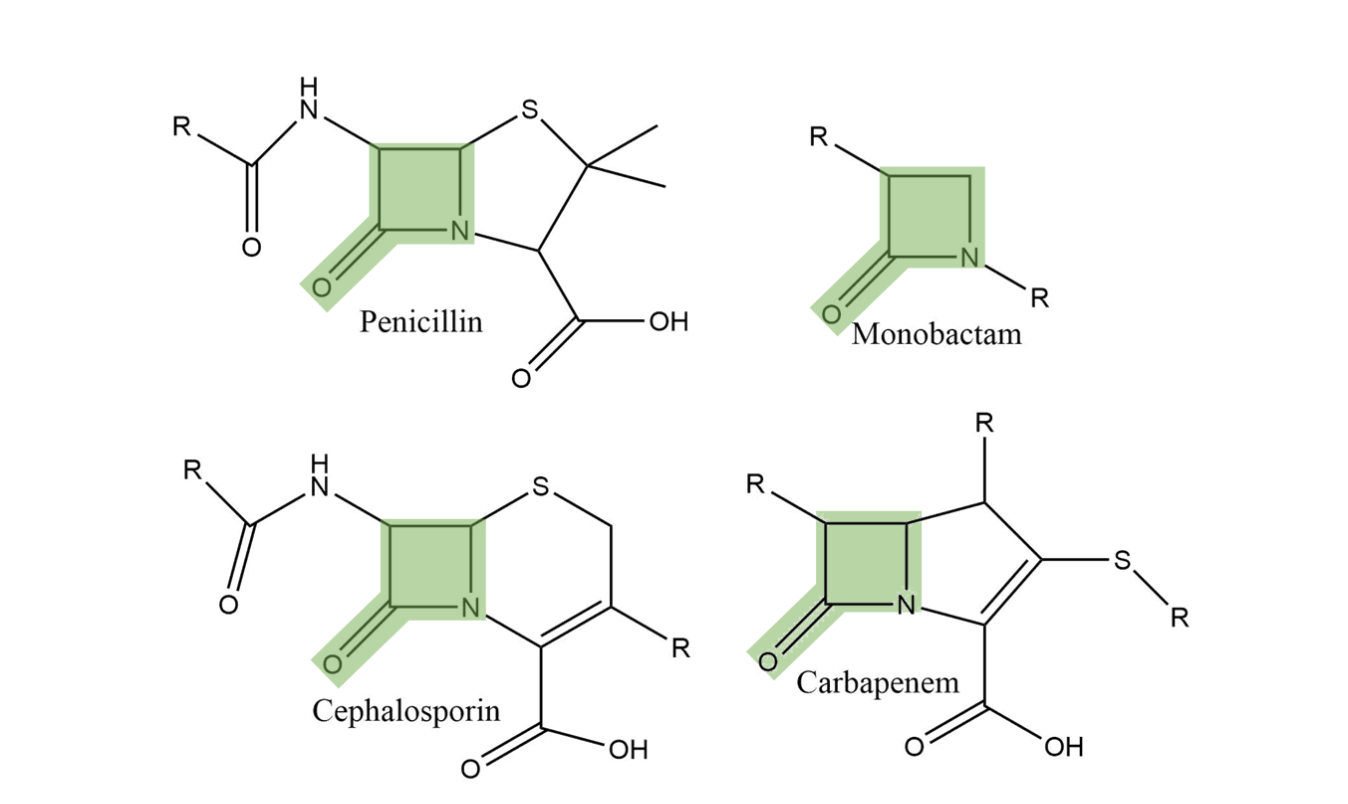
Bacterial Defense Mechanisms: MBLs
These antibiotics have been used abundantly for decades, and this has promoted bacteria to evolve mechanisms of defense against beta lactam antibiotics. To defend themselves, bacteria have evolved hydrolytic enzymes (enzymes that cut bonds using water) that break the beta-lactam ring. The most common class of these defensive enzymes is the metallo beta-lactamase (MBL). MBLs use a metal ion, typically zinc, in the enzyme active site to catalyze hydrolysis of beta lactam amide bonds, rendering the product ineffective as an antimicrobial agent.2 MBLs are able to hydrolyze nearly every beta-lactam, including the most recently developed carbapenems that have been elusive to most other bacterial defense enzymes. Additionally, MBLs are not deactivated by mechanism-based inhibitors like clavulanate or tazobactam that form an irreversible covalently-bonded complex with the enzyme.3 One MBL, New Delhi Metallo Beta-Lactamase (NDM-1), is of particular interest to scientists due to its rapid spread since its discovery in 2008 in New Delhi.2 (see Figure 2)
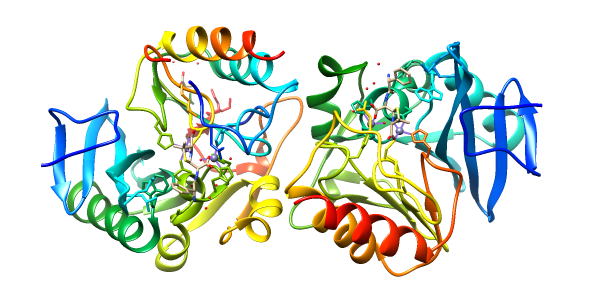
The plasmid-encoded NDM-1 gene (blaNDM-1) has been found in pathogenic Escherichia coli, Klebsiella pneumoniae and Acinetobacter baumannii as well as many other Gram-negative bacteria.4 NDM-1 can contain one or two metal ions but commonly functions with two zinc ions present in its active site. Evidence suggests that NDM-1 obtains the zinc from solution rather than during protein processing in the golgi.1 As seen in the figures, this enzyme is characterized by a ��β/β�� sandwich fold with the active site at the interface between domains.3
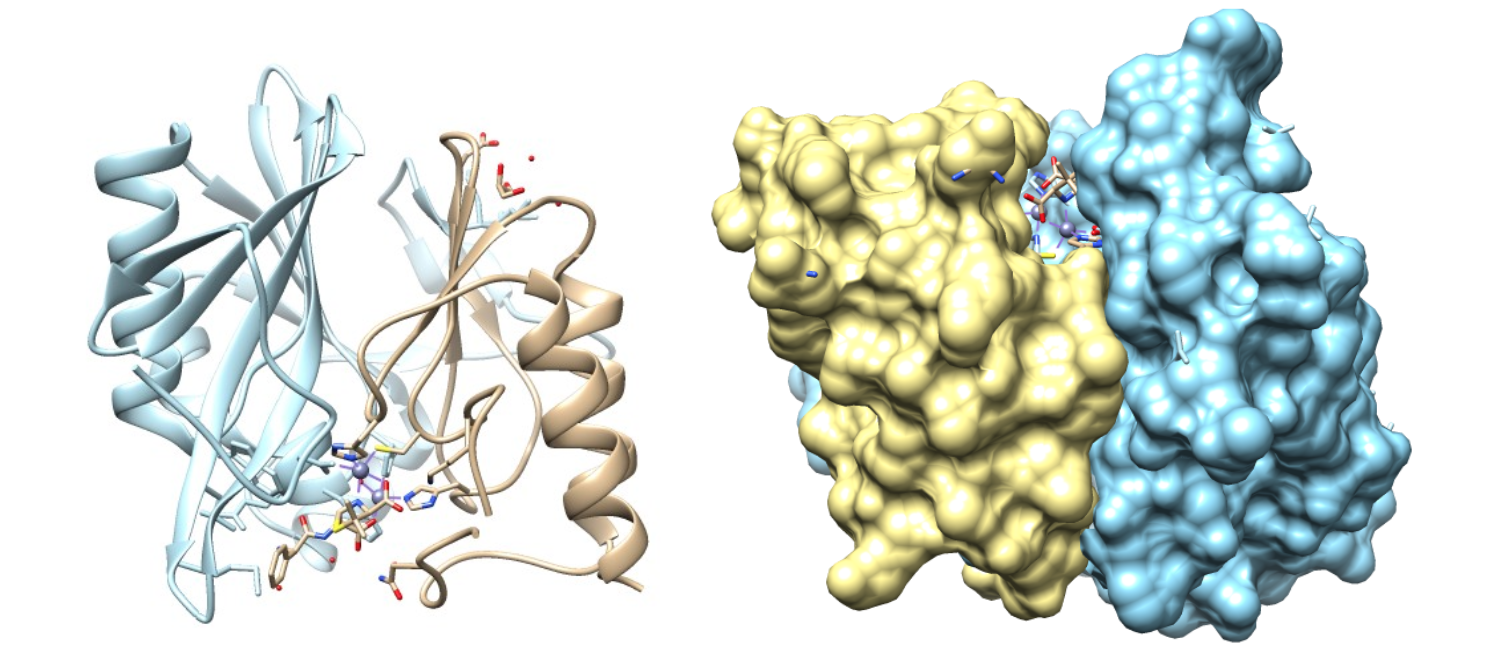
As shown above, the active site is in a deep cavity formed by two residual loops. This deep cavity allows for specificity and selectivity for the zinc ions.5 However, the area surrounding the active site is also very flexible. This flexibility is largely due to the high number of alanine residues (see figure below). Alanines have small side chain groups, which not only increases flexibility, but also decreases steric hindrance so that the active site can accommodate a wide range of beta-lactams that many other MBLs are unable to hydrolyze.4 The alanine-rich loops surrounding the active site help to position the antibiotic in such a way that the beta-lactam ring is right above the zinc ions, aiding in nucleophilic attack on the carbonyl carbon atom.7
As a chelating ligand, NDM-1 has a much higher binding affinity for any multiple metal ions than non-chelating ligands. The chelate effect describes the phenomenon where chelating ligands, those that are multidentate, such as NDM-1, have a much higher binding affinity for metal ions compared to monodentate ligands.6 This is due to entropy. The entropy, or disorder, of the universe can never decrease. To understand how this applies to metal ions and ligands, one must recognize that metal ions are typically bound to water in biological systems. When chelating ligands bind to metal ions, the water molecules are removed, thus resulting in more molecules in the products than were present in the reactants since each chelating ligand binds to more than one spot on the ion. More molecules in the products than the reactants means more disorder. In the case of NDM-1, the first zinc ion is coordinated to three histidines and a water molecule, making NDM-1 a tetradentate chelator with this zinc. The second chelator is coordinated to a histidine, an aspartic acid, a cysteine, and three water molecules, making NDM-1 a hexadentate chelator with this zinc.2
Zinc Selectivity and Specificity
While the area surrounding the active site is flexible and can accommodate several different metal ions, demonstrating the versatility of NDM-1, this enzyme remains selective for zinc(II) ions. In fact, because of the flexibility of the active site, NDM-1 can bind to and is catalytically active using a variety of metals including iron, cobalt, cadmium, and manganese. Experimental data has shown that the substrate binds with similar affinity to NDM-1’s active site regardless of metal combinations.8 Yet, when placed into solution with both iron and zinc, NDM-1 preferentially binds to zinc.5 Additionally, NDM-1 has only been found bound to zinc in bacteria.
1) Ionic Radii
One common consideration for preferential binding is ionic radius. If an ion is too big or too small, it may not be appropriate for the active site of that particular enzyme. When looking at the ionic size of several ions that have been tested with NDM-1, there is some variability (see tabulated data below).
Table 1: Ionic radii of metal ions found complexed with NDM-1 in the tetrahedral and octahedral geometries9
|
Metal |
Tetrahedral Geometry (pm) |
Octahedral Geometry (pm) |
|
Cadmium(II) |
92 | 109 |
|
Cobalt(II) |
72 | 88.5 |
|
Iron(II) |
77 | 92 |
| Manganese(II) | 80 | 97 |
| Zinc(II) | 74 | 98 |
As shown by the above data, iron(II) and cobalt(II) have very similar ionic radii to zinc(II) while cadmium(II) and manganese(II) are significantly different from zinc(II). Thus it is unlikely that ionic radius is the only determining factor for metal ion selectivity.
2) Effective Nuclear Charge (Zeff)
Another consideration is the effective charge (Zeff) or the electrostatic charge experienced by each metal’s outermost electrons, which is mostly ordered by the Irving-Williams series (see figure below). The Irving-Williams series is explained by a combination of Zeff and LFSE. Zn(II) has a larger Zeff than any of the other first row transition metals and thus should have a higher affinity than any of them. The reason that Cu(II) has a higher affinity than Zn(II) is due to the Jahn-Teller effect, a distortion of the octahedral geometry that affords Cu(II) additional stability and thus higher affinity.6
Mn(II) < Fe(II) < Co(II) < Ni(II) < Cu(II) > Zn(II)
As can be seen from the series, and explained by this periodic trend, zinc(II) should be the most attracted to the ligands of NDM-1, with the exception of Cu(II), partially explaining the selectivity of NDM-1 for zinc(II).
3) LFSE
A third consideration is ligand field theory (LFT) and its ligand field stabilization energy (LFSE). LFT explains the preferred octahedral geometry of most metal complexes due to d orbital splitting. With either tetrahedral or octahedral geometry, the two most common geometries, the d orbitals split to form two energy levels: t2 and e for tetrahedral or t2g and eg for octahedral. Transitions between these two d orbital energy levels cause the distinct colors in transition metal complexes. However, the amount of electrons present in each energy level differs based on the geometry (see Figure 5 below).
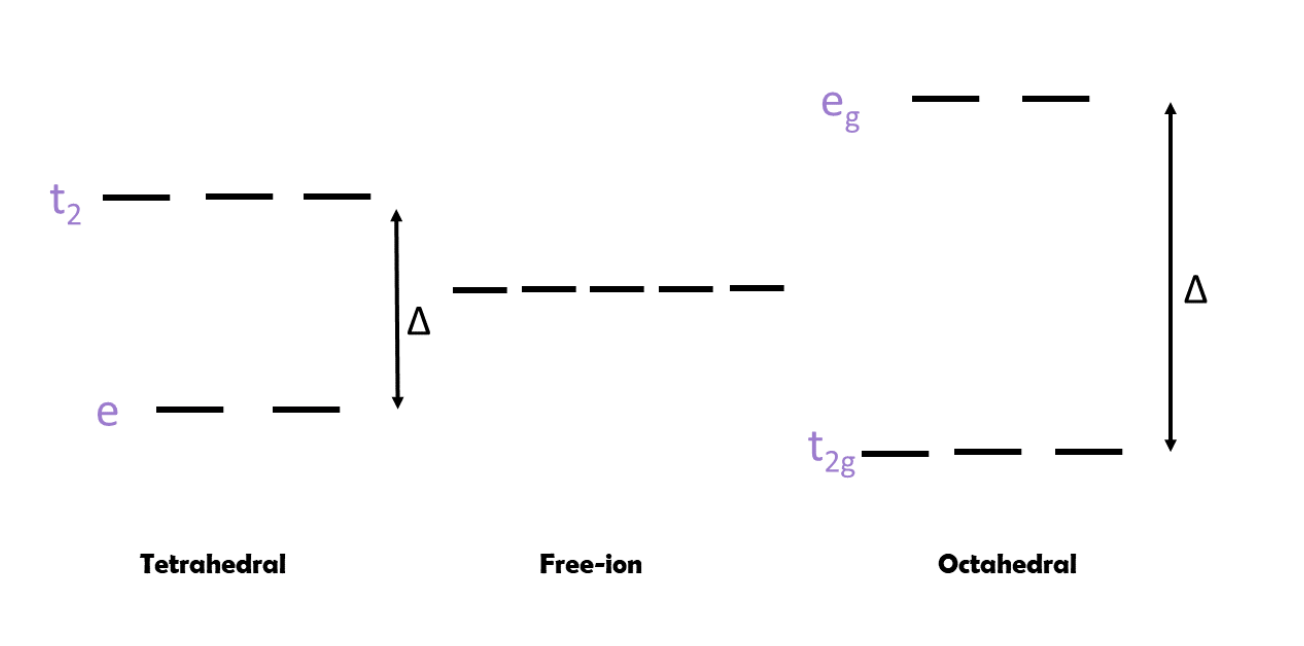
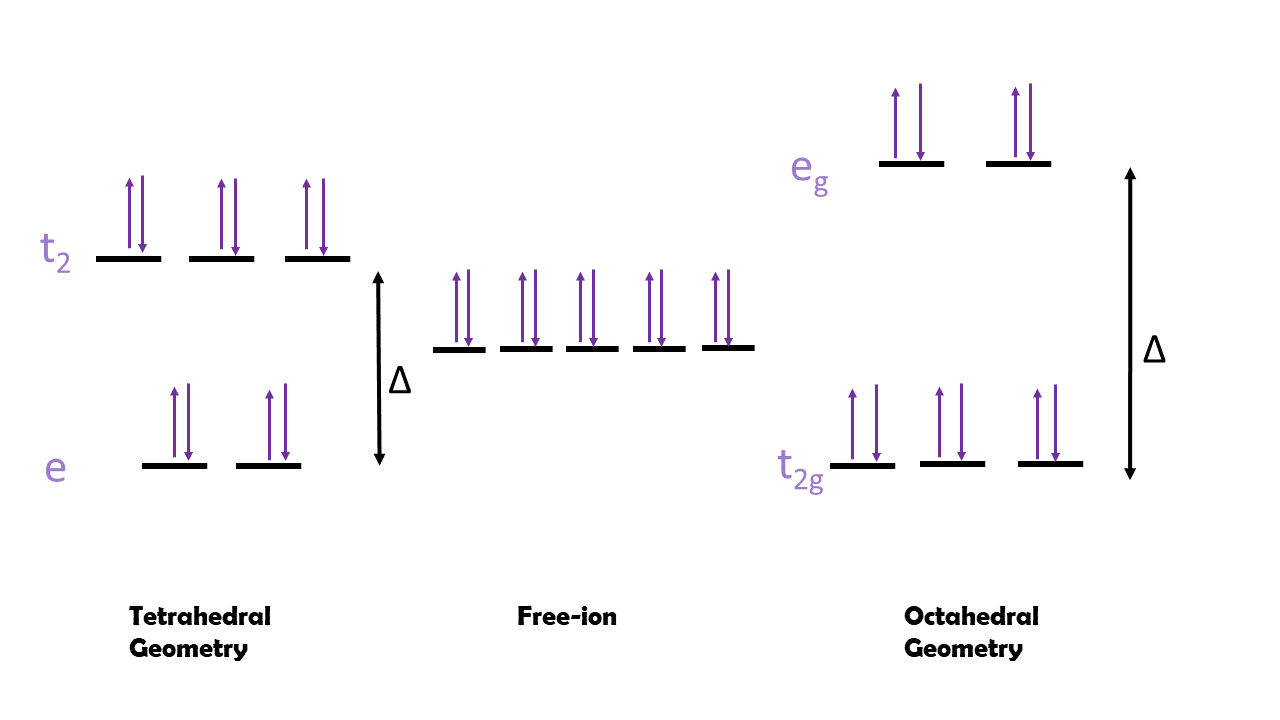
When the metal centers have octahedral geometry, the complexes may have two ways to fill electrons into orbitals; if this is the case they are either high spin or low spin. High spin complexes occur when the Δ is fairly small and the energy required to go into the eg orbitals is not great enough to overcome the repulsion of pairing two electrons in the same orbital. In contrast, low spin complexes occur when Δ is large and the repulsive energy required to obey Hund’s Rule and maximize spin is not greater than the energy required to jump from t2g to eg. There are several factors that determine if a metal complex will be high spin or low spin, including the identity of the metal: which metal is involved, the charge on the metal, and how large the metal is. Typically, metals in the first row have a much higher likelihood of forming high spin complexes than those in rows 2-3. Additionally, a larger charge on the complex tends to result in larger Δ and low spin complexes.6
However, when looking at the electron filling diagram of zinc, there are 10 d-electrons present in the valence orbital. Thus, there is no high spin and low spin case because there is only one way to fill the orbitals. Thus, the other main consideration is which ligands are complexing to the metal. The imidazole nitrogen of histidine is a sigma donor and a pi acceptor, classifying it as a strong field ligand that increases Δ. The carboxylic acid oxygen on aspartic acid is a sigma donor and pi donor, classifying it as a weak field ligand that decreases Δ. The sulfur on cysteine is a sigma donor and pi donor as well, classifying it as a weak field ligand that decreases Δ. The oxygen on water is also a sigma donor and pi donor but it lies in the middle of the spectrochemical series so it is classified as a weak-medium field ligand. Based on these classifications, the zinc bonded to the three histidine residues should have a large Δ and be low spin because of the strong field produced. The water isn’t weak enough to decrease the Δ that significantly. In contrast, the other zinc that is bonded to the histidine, cysteine, aspartic acid, and three waters will likely have a small-medium Δ and be high spin because of the weak field produced.
Once the field strength has been determined for a system, the ligand field stabilization energy (LFSE) for an octahedral geometry can also be obtained by the following formula:
LFSE=(-0.4x +0.6y)Δ
Here, x represents the number of electrons in the t2g orbitals and y represents the number of electrons in the eg orbitals. As shown below, zinc(II) has 10 d electrons which completely fills both sets of orbitals. Thus, the LFSE is 0.
The LFSE for a tetrahedral geometry can also be determined by approximating the Δ for tetrahedral to be 4/9 that of the Δ for octahedral. Alternatively, it can be calculated using the following equation where x represents the number of electrons in the e orbitals and y represents the number of electrons in the t2 orbitals.
LFSE=(-0.6x +0.4y)Δ
In this particular case, the LFSE is still 0 either way. Typically, the more negative LFSE determines the more stable geometry that will be found in nature. However, because both are 0 in this case, it is impossible to determine the favored geometry based solely on LFSE. There are other factors that can help determine the geometry such as sterics and the size of the ligands.
The other metals that complex with NDM-1 have different LFSE values (see table below) that determine the preferred geometry for each of these metals.
Table 2: LFSE calculations and preferred geometry for various metal ions found complexed with NDM-1
| Metal | Tetrahedral LFSE | Octahedral LFSE | Preferred Geometry |
| Cadmium(II) | 0 | 0 | Neither based on LFSE |
| Cobalt(II) | -1.2Δ | -0.8Δ | Octahedral |
| Iron(II) | -0.6Δ | -0.4Δ | Octahedral |
| Manganese(II) | 0 | 0 | Neither based on LFSE |
| Zinc(II) | 0 | 0 | Neither based on LFSE |
Based on the above information, while it appears that cobalt(II) would be preferred over iron(II) due to the LFSE, overall the data is fairly inconclusive given the d10 and d5 metals involved. Thus, it is necessary to go one step further and explore Hard Soft Acid Base (HSAB) Theory to help explain NDM-1’s preference for zinc.
4) HSAB Theory
HSAB Theory categorizes metals and ligands into “hard” or “soft” based on multiple characteristics. Hard acids and bases have more electrostatic interactions, tend to have a higher charge density, are smaller ions, and are less polarizable compared to soft acids and bases that have a strong covalent bonding component, are more polarizable, are typically larger ions, and have a lower charge density. In the first row of transition metals, there are hard, borderline, and soft acids. The further towards the first two columns of the periodic table each atom is, the harder it is.6 Zinc is a borderline acid and it is the softest of the 3d metals with +2 charge due to its position on the periodic table. The hard/soft character of the other metals that coordinate with NDM-1 are also given below.
Table 3: HSAB theory characteristics of various metals found complexed with NDM-1
| Metal Ion | Hard/Soft/Borderline |
| Cadmium(II) | Soft |
| Cobalt(II) | Borderline |
| Iron(II) | Borderline |
| Manganese(II) | Borderline/Hard |
| Zinc(II) | Borderline (Softest of these examples) |
In HSAB theory, like attracts like. Thus, hard acids attract hard bases, etc. According to this theory, zinc is most likely to be attracted to borderline bases or soft bases. This is true on the NDM-1 active site. The first zinc ion is thought to coordinate with three histidine residues and a water molecule. Histidine has an imidazole ring that is characterized as a borderline base, perfect for coordinating with zinc. Water is classified as a hard base, which seems to contradict HSAB theory. However, it has been noted that zinc can act as a hard acid in aqueous environments in order to coordinate with water.8 It must be remembered that this first zinc only coordinates with the water molecule to stabilize it and catalyze the hydrolysis of the antibiotic. Thus, it need not coordinate with it during any other time. The second zinc ion coordinates with a histidine, aspartic acid, a cysteine, and three water molecules. The histidine again has the ideally borderline base imidazole ring, the cysteine has sulfur (which is a soft base), and the aspartic acid has a carboxylic acid group with two oxygens, which are typically considered to be hard bases, and again the water is a hard base. However, it has been observed that the first zinc ion is much more strongly coordinated than the second one, and this may be explained by HSAB theory.4 The second zinc would coordinate strongly to the soft and borderline bases but would be less happy coordinating with the hard bases. Additionally, the borderline-soft character of zinc, in comparison with the hard-borderline character of the other metals, likely helps NDM-1 be more selective for zinc, though this is not discussed explicitly in the literature.
Now that metal ion selectivity has been discussed, it is necessary to examine the active site itself and the catalytic cycle that results from the activity of NDM-1. However, there is some discrepancy in the literature regarding both the geometry of the active site and the exact mechanism of the catalytic cycle.
Active Site Geometry
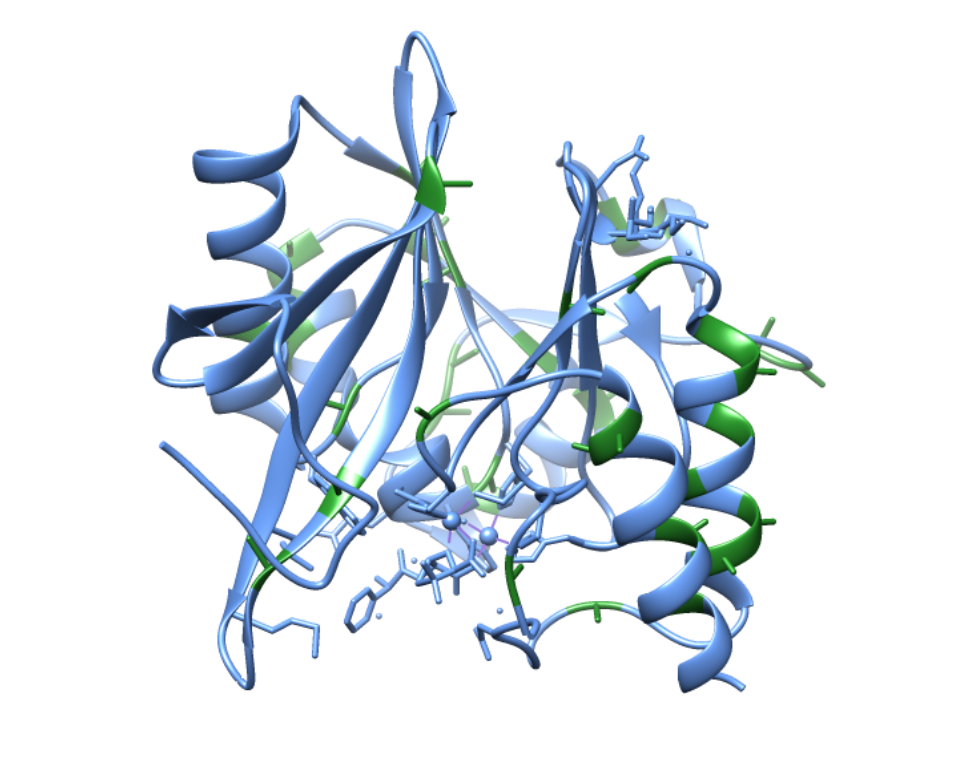
According to some literature, one of the zinc ions (Zn1) is coordinated by three histidine residues while the other (Zn2) is coordinated by aspartic acid, cysteine, and histidine residues. The first zinc ion is also coordinated by a water molecule which acts as the nucleophile when attacking the β-lactam.2 (see Figure 7 below).
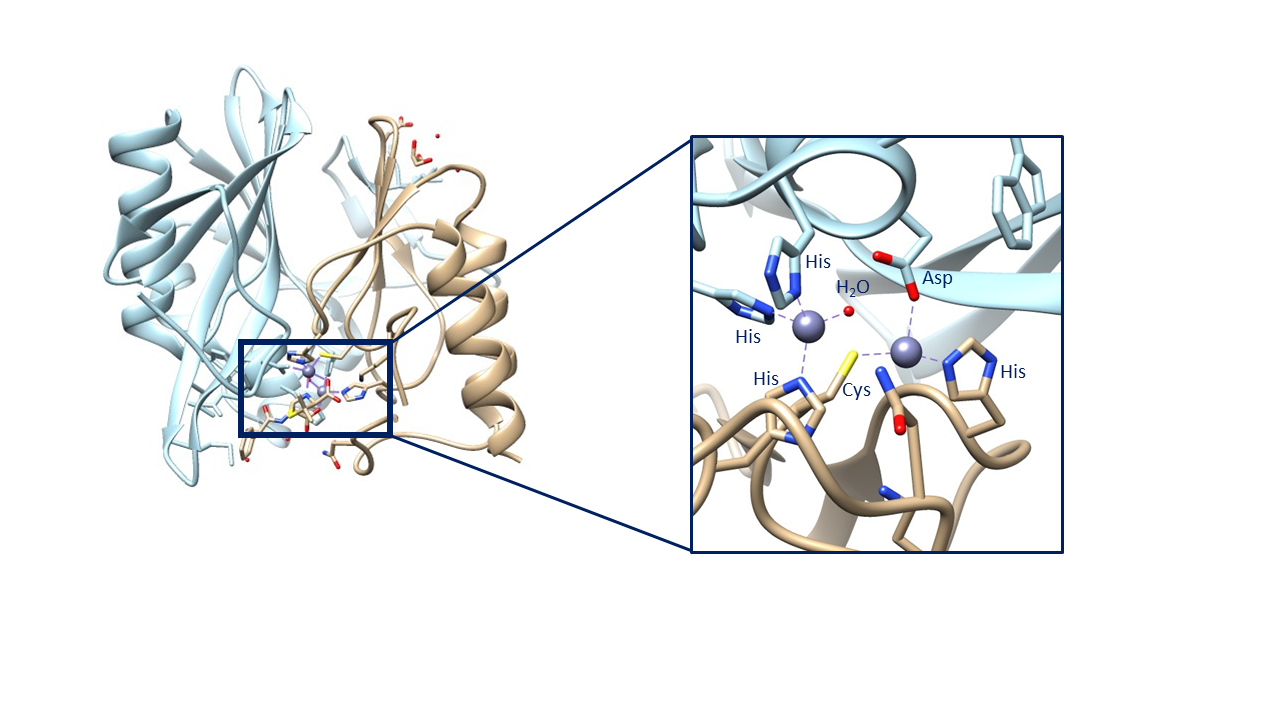
Alternatively, some literature argues that, based on the mechanistic and spectroscopic studies performed, the geometry of the two zinc ions is different than found in the above crystal structure. This argument is largely due to collected crystal structures such as the one shown above. This crystal structure contains the zinc ions complexed with a hydrolyzed ampicillin substrate and, when the beta-lactam is removed, this is the geometry that remains. It seems unlikely that the geometry would not shift at all during the catalytic cycle, thus other geometries have been proposed. However, no crystal structure has been obtained with two zincs unless they are complexed with a beta-lactam. The crystal structure of NDM-1 has also been obtained with no zincs or with one zinc. Lastly, and most significantly, the crystal structure of NDM-1 has been obtained with one zinc in the Zn1 position and a cadmium in the Zn2 position. This causes a tetrahedral geometry for the Zn1 ion, complexed with the same three His residues and nucleophilic water molecule. However, the cadmium is complexed to three water molecules in addition to the His, Cys, and Asp residues, forming an octahedral geometry (see figure below).
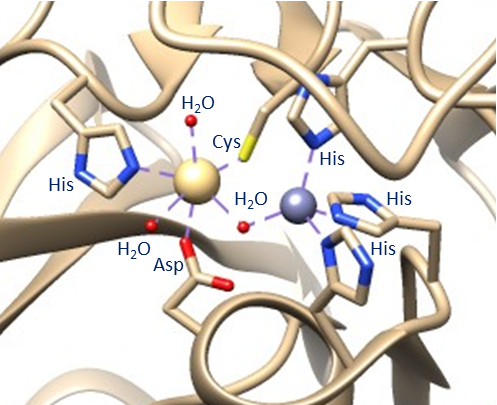
Because no one has been able to obtain a single crystal structure of NDM-1 with only the two zincs, its exact geometry is elusive.
Catalytic Mechanism
As mentioned above, there is also dispute about the mechanism of the catalytic cycle. The reaction scheme itself is fairly straightforward (see figure below): the beta-lactam is hydrolyzed by a water molecule that has been activated by NDM-1.
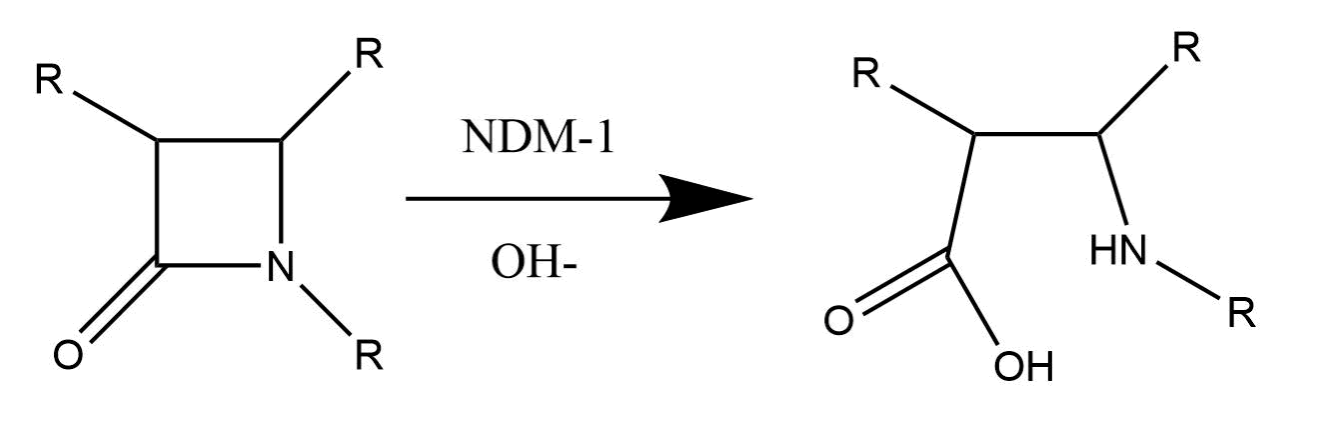
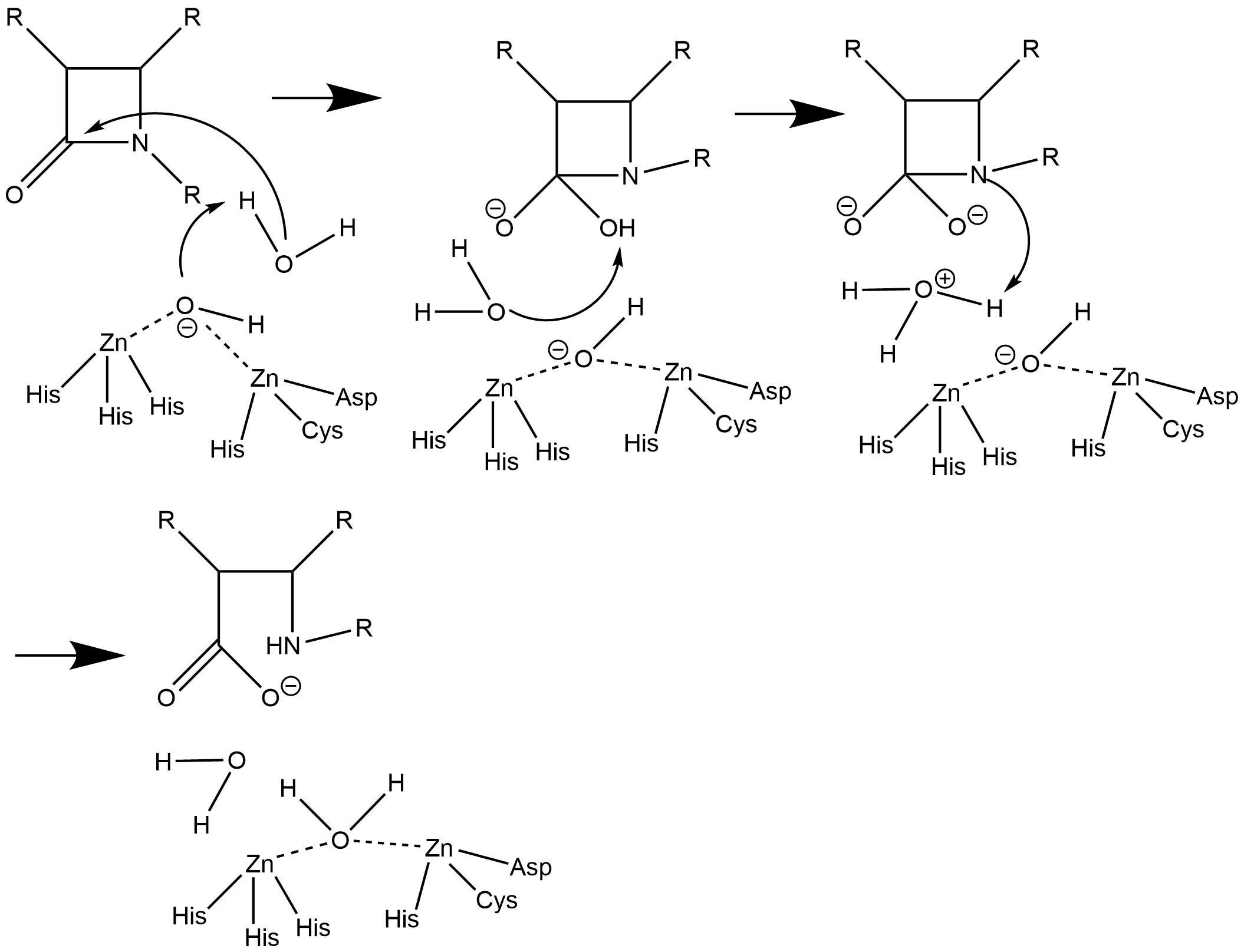
The overall mechanisms are fairly similar but there is dispute about the role of the second zinc ion (Zn2). In the first mechanism (see figure below), the second zinc is only present to help stabilize the bridging water molecule that activates a chain of other water molecules that eventually hydrolyze the beta-lactam.
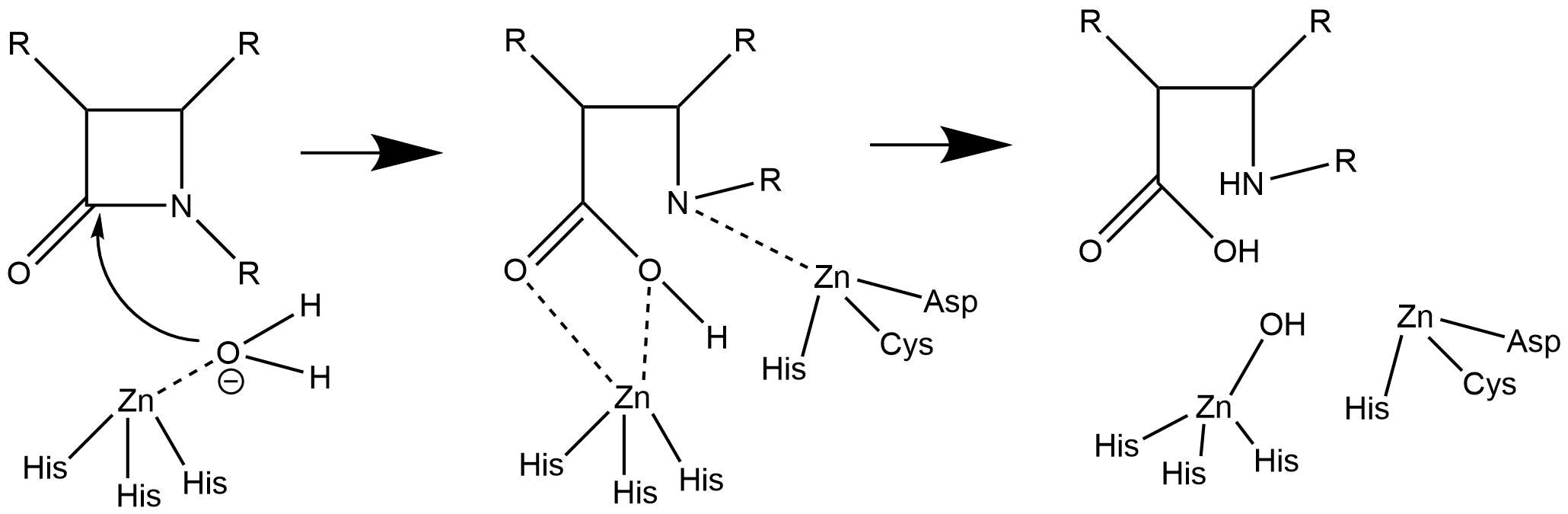
In contrast with this above mechanism, a simpler mechanism has a more active role for both zinc ions (see figure below). In this mechanism, the first zinc both stabilizes the nucleophilic water molecule and helps to stabilize the carbonyl oxygen atom. The second zinc stabilizes the nitrogen atom as well.
The latter mechanism may be more likely based on the coordination chemistry of the crystal structures obtained that involve zinc ions and hydrolyzed beta-lactams.
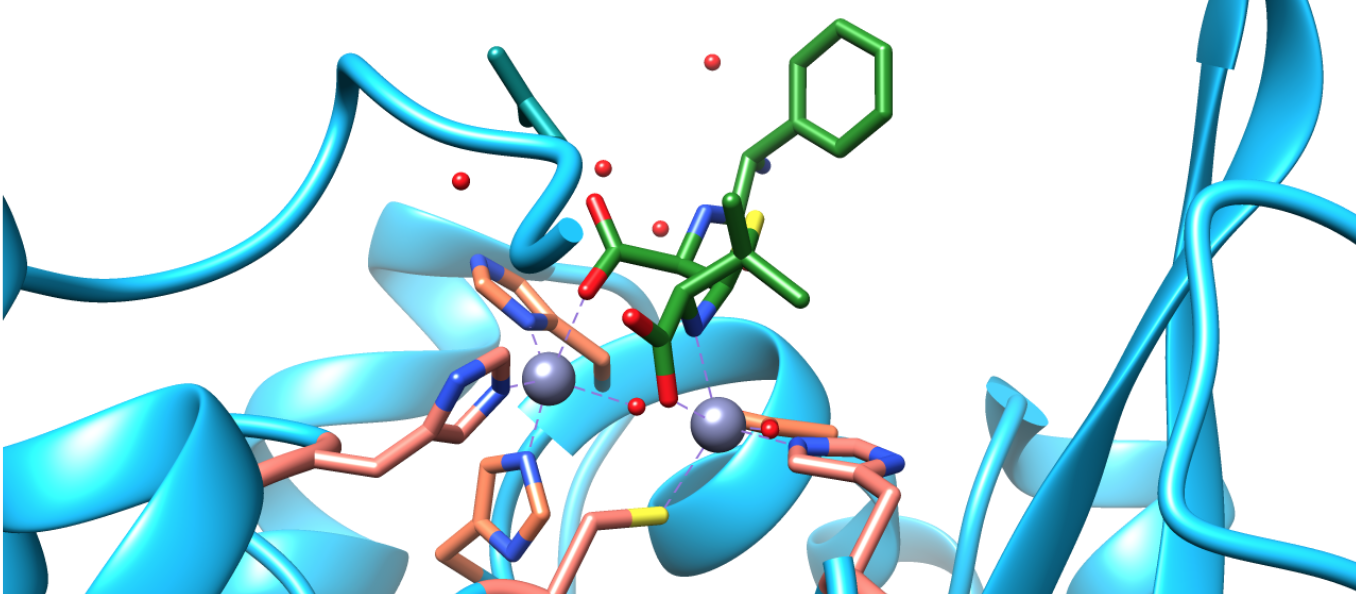
Based on this crystal structure data, it appears as though the zinc ions coordinate with the beta-lactam either during or after hydrolysis. Therefore, it is possible, if not probable, that the zincs are able to stabilize the nitrogen and oxygen of the beta-lactam ring during hydrolysis, lending credence to the second mechanism shown.
Why does this catalytic cycle take place? This can be explained by several chemical principles. Firstly, the electrostatic interaction of the electron density attraction between the ions is significant enough to even form these coordination complexes between the zinc ions and their ligands, as well as between the zincs and the atoms of the hydrolyzed beta-lactam.
Secondly, the pKas involved are also relevant. pKa is one way of describing how acidic or basic a molecule is and helps in understanding the mechanism of a reaction. The pKa of water without anything else interacting with it is 14. Lowering the pKa of a molecule makes it more acidic. Metal ions are Lewis Acids that are especially well-suited for binding to water and lowering its pKa.6 The zinc ions in NDM-1 activate a water molecule so that the deprotonated water (hydroxyl group) can act as a nucleophile and attack the carbonyl carbon of the beta-lactam ring. The zinc ions stabilize the hydroxide, lowering its pKa, which lowers the activation energy of the nucleophilic hydrolysis reaction and thus catalyzes the reaction. If the second zinc were to be replaced with a cobalt ion, a more acidic transition metal ion than zinc, the intermediate of the activated water molecule is formed faster than when zinc is present. Thus, the cobalt can stabilize the hydroxide and lower its pKa further than zinc. However, when cadmium, a weaker Lewis acid than zinc, replaces one of the zinc ions, the intermediate forms slower, demonstrating that the hydroxide is stabilized less than with zinc.8
Lastly, electron count is a way of describing the number of electrons of the valence shell of a transition metal at the center of a coordination complex. Often, metal catalysts are at either 16 or 18 valence electrons as catalysis is performed. Zinc is redox inactive and always maintains a charge of +2. Thus, in the case of NDM-1, both zinc ions have an electron count of 16 when bonded solely to the three amino acid residues. When also bonded to the water molecule(s), the first zinc has an electron count of 18 and the second zinc has an electron count of 18 or 22, depending on which proposed geometry is actually present. This classic 16/18 cycle reiterates the actuality of the catalytic cycle of NDM-1.
In conclusion, NDM-1 is a potent beta-lactamase that can hydrolyze nearly any beta-lactam antibiotic. Its properties and behavior can be explained through chemical principles and theories such as HSAB Theory and Ligand Field Theory. There are many things still to learn about NDM-1 to effectively design medical treatments that can inhibit both NDM-1 as well as all other MBLs.
Sources
- Karsisiotis, A. I.; Damblon, C. F.; Roberts, G. C. K. A Variety of Roles for Versatile Zinc in Metallo-β-Lactamases. Metallomics 2014, 6 (7), 1181–1197.
- Zhang, H.; Hao, Q. Crystal Structure of NDM-1 Reveals a Common β-Lactam Hydrolysis Mechanism. The FASEB Journal 2011, 25 (8), 2574–2582.
- Palzkill, T. Metallo-β-Lactamase Structure and Function. Annals of the New York Academy of Sciences 2013, 1277 (1), 91–104.
- Kim, Y.; Tesar, C.; Mire, J.; Jedrzejczak, R.; Binkowski, A.; Babnigg, G.; Sacchettini, J.; Joachimiak, A. Structure of Apo- and Monometalated Forms of NDM-1—A Highly Potent Carbapenem-Hydrolyzing Metallo-β-Lactamase. PLOS ONE 2011, 6 (9), e24621.
- Hu, Z.; Gunasekera, T. S.; Spadafora, L.; Bennett, B.; Crowder, M. W. Metal Content of Metallo-β-Lactamase L1 Is Determined by the Bioavailability of Metal Ions. Biochemistry 2008, 47 (30), 7947–7953.
- B. Chelate and Macrocycle Efect https://chem.libretexts.org/LibreTexts/Saint_Mary’s_College%2C_Notre_Dame%2C_IN/CHEM_342%3A_Bio-inorganic_Chemistry/Chapters/Chapter_2%3A_Introduction_to_Metal-Ligand_Interactions/2.3_Ligands_with_more_than_one_donor_atom_(Chelating_Ligands)/B._Chelate_and_Macrocycle_Efect (accessed Feb 7, 2018).
- Tamilselvi, A.; Mugesh, G. Zinc and Antibiotic Resistance: Metallo-Beta-Lactamases and Their Synthetic Analogues. Journal Of Biological Inorganic Chemistry: JBIC: A Publication Of The Society Of Biological Inorganic Chemistry 2008, 13 (7), 1039–1053.
- Yang, H.; Aitha, M.; Marts, A. R.; Hetrick, A.; Bennett, B.; Crowder, M. W.; Tierney, D. L. Spectroscopic and Mechanistic Studies of Heterodimetallic Forms of Metallo-β-Lactamase NDM-1. J. Am. Chem. Soc. 2014, 136 (20), 7273–7285.
Contributed by
This work was originally written by Heather DiLallo, Spring 2018: Heather is currently (as of 2018) a junior chemistry major at Saint Mary's College in Notre Dame, IN.
This work was originally edited by Dr. Kathryn Haas (Assistant Professor), Madison Sendzik (Teaching and Research Assistant), and Dr. Dorothy Feigl (Professor) at Saint Mary's College.


