Methane Monooxygenase
- Page ID
- 212599
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
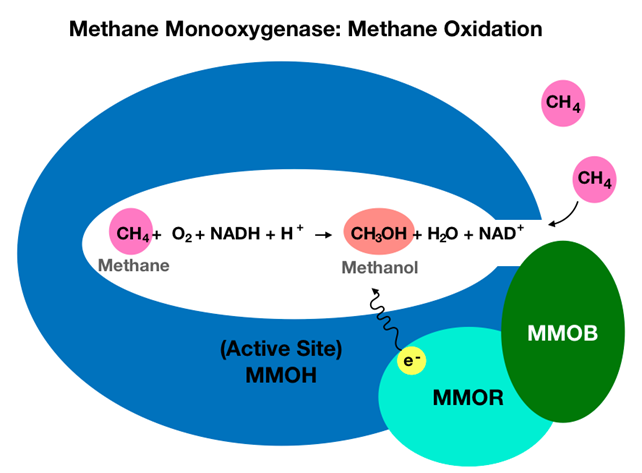
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)MMO in these methanotrophs exists as soluble methane monooxygenase (sMMO) or as particulate methane monooxygenase (pMMO), both of which allow for selective hydroxylation of methane. The sMMO is soluble in water, contains iron, and can be found in the cytoplasm of bacterial cells.1 The pMMO is an intracytoplasmic membrane protein that contains copper.1,2,4 Here intracytoplasmic membrane refers to part of the bacterial membrane that extends inward into the cytoplasm.5 Compared to sMMO, pMMO has a higher affinity for the enzyme’s \(\ce{O_{2}}\) and \(\ce{CH_{4}}\) substrates, making pMMO a more active enzyme than sMMO.1 However, because the membrane-bound protein has proven to be more difficult to study in vitro, this article will focus on the more widely understood sMMO, herein referred to as MMO. Soluble methane monooxygenase is classified as an enzyme complex that contains multiple protein components. More specifically, these components include a 245 kDa hydroxylase protein (MMOH), a 40 kDa reductase protein (MMOR), and a 16 kDa regulatory protein (MMOB) that work together to allow for oxidation of methane to methanol, shown below in Figure 1.6 The MMOB regulates the enzyme’s catalytic activity via allosteric regulation, meaning MMOB binds to MMOH to create a shift in the molecular shape of MMOH to control substrate access to the MMOH active site. Since substrates are required for catalytic activity, this binding is necessary for methane hydroxylation. MMOR receives electrons from NADH to reduce the irons found in the active site of MMOH.
In light of existing studies, analysis of MMO structure and binding site through the lens of bioinorganic chemistry can give rise to additional understanding of MMO catalytic efficiency. This article introduces the overall structure of MMO, focuses on the diiron active site, elaborates on methane oxidation catalysis, and discusses metal coordination using bioinorganic chemistry concepts.
Methane Monooxygenase Structure
The sMMO is an enzyme complex composed of three components that work together to complete methane oxidation. Shown in Figure 2, components include a hydroxylase (MMOH) to oxidize the substrate, a reductase (MMOR) to transport electrons to the enzyme active site, and a regulatory protein (MMOB) that contributes to the catalytic efficiency of MMO. Coenzymes, non-proteins or metallic ions that contribute to the catalytic function of another protein, for MMOR include flavin adenine dinucleotide (FAD) and nicotinamide adenine dinucleotide (NADH) that transfer electrons to reduce the Fe ions in MMOH, seen below in Figure 2. The MMOB component does not contain cofactors, see Figure 2, but the binding of MMOB to MMOH changes MMOH’s conformation to open a pore for substrate access to the active site.2 Substrates include molecular oxygen (\(\ce{O_{2}}\)) and methane (\(\ce{CH_{4}}\)). Thus, MMOB orchestrates oxygen activation coupled with \(\ce{CH_{4}}\) oxidation.1 Figure 2 below shows structures of MMOB and MMOR.

The MMOH is composed of 3 subunits \(\alpha\), \(\beta\), and \(\gamma\). Both MMOB and MMOR bind to the \(\alpha\) subunit of MMOH at a binding site called a canyon region. The details of MMOR binding are under debate, but some studies suggest MMOR and MMOB bind competitively to this canyon region. In this case, MMOR binds to MMOH to reduce the diiron cluster. Subsequently, MMOB displaces MMOR to commence the catalytic cycle, MMOB remains bound to MMOH throughout the catalytic cycle and prevents MMOR from rebinding.6 As the regulatory protein, MMOB binds to this canyon region to induce a conformational change in the MMOH protein. The resulting MMOH-MMOB complex has a pore that allows substrates to access the active site. Figure 2 above shows where MMOB binds to MMOH. Homodimer subunits of MMOH consist of a diiron bridged at the active site.1 For the MMOH that oxidizes the substrate, iron is the important cofactor. Figure 2 above shows MMOH along with two identical diiron active sites.
Methane Monooxygenase Active Site
This article will focus on the diiron active site of MMOH, where methane oxidation occurs. While the steps of methane hydroxylation entail formation of a series of intermediates, the resting state MMOH is typically used to depict the diiron active site. At resting state, before any substrates are bound to the enzyme, the two irons both exist as Fe(III) ions and the complex is considered to be oxidized (MMOHox).3 As seen in Figure 3, the irons are pseudo-octahedrally coordinated to solvent molecules along with glutamate and histidine residues. Pseudo-octahedral coordination refers to a complex that does not have perfect octahedral angles, but that follows octahedral complex behavior in terms of orbital splitting.

The Fe(III) ions within MMOH are coordinated to oxygen atoms from glutamic acid (Glu) and solvent molecules, and to imidazole nitrogen atoms from histidine (His) (Figure 3). Throughout the catalytic cycle, the diiron cluster at the active site of MMOH undergoes oxidation-reduction (redox) reactions in which the iron loses (oxidation) and gains (reduction) electrons. Figure 4 compares the coordination of the resting state (MMOHox) and the first intermediate of the cycle (MMOHred). MMOHox becomes reduced to MMOHred, upon acquisition of two electrons from MMOR, to yield two Fe(II) ions.1 At the MMOHox resting state, one Fe(III) is coordinated to Glu114, His147, His144, water, and two hydroxide solvent molecules. The other Fe(III) is coordinated to Glu209, Glu243, His246, and two hydroxides. The two hydroxides and Glu144 help bridge the two Fe(III) ions.1 Reduction in each of the iron ions coincides with loss of one hydroxide and a ligand exchange from the oxygen of hydroxide to the oxygen of Glu243. In reduced MMOHred, the Fe(II) ions are connected by two Glu144 and Glu243 instead of by hydroxide, water, and Glu144.1 Figure 4 below depicts these distinctions.

MMOHox is a polydentate chelator that is tridentate for one iron and tetradentate for the other iron. Here a polydentate chelator refers to a ligand that is coordinated to the metal through more than one atom, indicated by a number prefix to describe dendicity. Overall MMOHox coordinates to 6 ligands. MMOHox is a polydentate chelator that is tetradentate for one Fe(II) and pentadentate for the other Fe(II). The MMOHred contains reduced Fe(II) that coordinates to 6 ligands. MMOHred is tetradentate for one Fe(II) and pentadentate for the other; among the ligands, Glu243 bidentate for this Fe(II). Investigations of the apo-enzyme, meaning the protein without the iron cofactors, indicate MMOH subunits require iron to fold properly.7
Methane Monooxygenase Catalytic Activity
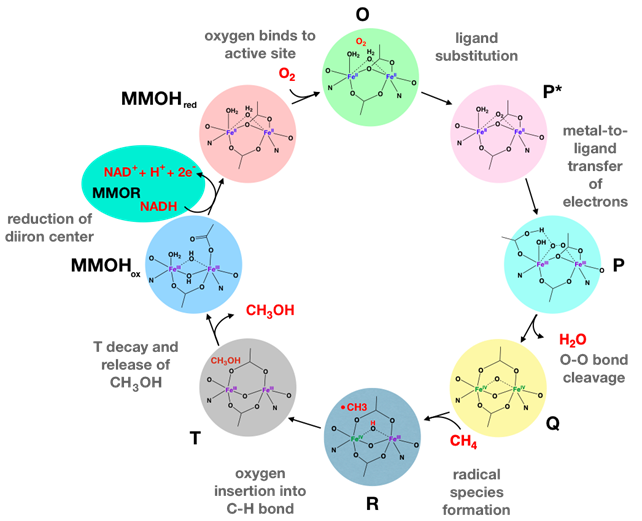
Methane oxidation occurs in the MMOH protein of MMO where a series of intermediates are formed. The catalytic cycle is depicted in Figure 5. MMO is considered a dioxygen activating enzyme because MMO’s catalytic cycle entails oxygen activation, which refers to reactions between a transition metal like Fe and oxygen, in which oxygen acts as a substrate for metal-oxygen intermediates.8 Oxygen activation is prevalent in biological reactions, particularly in oxidative metabolism, such as \(\ce{CH_{4}}\) oxidation.9 This step occurs in MMO’s catalytic cycle after MMOHox is reduced to MMOHred. Upon reduction, Fe(II) in MMOHred loses an electron to \(\ce{O_{2}}\) to yield an intermediate called O. At this point \(\ce{O_{2}}\) binds irreversibly to the enzyme active site but is not directly bound to the diiron cluster. Without MMOB, this reaction is extremely slow and inefficient. With MMOB the rate constant of \(\ce{O_{2}}\) activation increases by a factor of 150. Subsequently a ligand exchange occurs to yield a recently proposed antiferromagnetically coupled odiiron(III)-peroxo species (P*). An antiferromagnetically coupled diiron(II)-peroxo intermediate (P) is formed as the bridging peroxide is reduced and the diiron cluster is oxidized. The next intermediate, Q, is formed by proton-promoted cleavage of the O-O bond and rearrangement of the diiron center. Intermediate Q has a diiron core with Fe(IV) irons and is capable of direct methane oxidation. Recent literature has proposed that intermediate Q inserts an oxygen atom into a C-H bond of methane through formation of species R. Species R forms as a hydroxyl radical binds to the diiron cluster to leave a methyl radical (•\(\ce{CH_{3}}\)). The radicals recombine to form species T, a bound methanol product complex. Finally, decay of T releases methanol and reforms MMOHox as the rate-limiting step of the reaction.
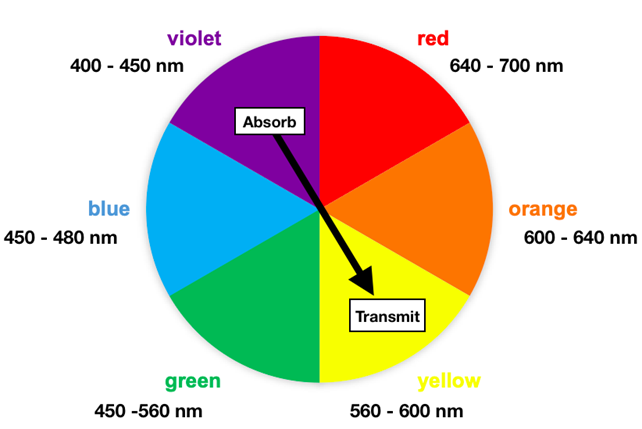
Studies have indicated that MMOH is colorless in the visible spectral region.11 Among all the intermediates, Q has been described as yellow in color.12 Visible light wavelengths range from approximately 400 nm to 700 nm, where each wavelength corresponds with a color. Humans perceive transmitted light, reflected light, or both. The color transmitted is complementary to an absorbed color, often depicted on a color wheel. Figure 6 shows a color wheel with corresponding absorbed and transmitted colors located across from one another. Only Q’s 430 nm wavelength is within the visible light wavelength range. Intermediate Q absorbs in the violet wavelength range (400 -450 nm) and transmits in the yellow wavelength range (560 - 600 nm). Thus, intermediate Q appears yellow. Other intermediates have not been characterized.
Metal Coordination
HSAB Theory
Hard-soft acid-base theory (HSAB) can be used to predict which atoms are more compatible acid-base pairs based upon properties including the charge to size ratio, polarizability, and covalent nature of bonding. Atoms with “hard” character generally have high charge density and form bonds that are more ionic in nature. Atoms that are “soft” generally have lower charge densities and result in bonds that are more covalent. Hard acids, are more likely to combine with hard bases and vice versa; however, there are exceptions to the rules because of other factors that need to be considered that are unrelated to hardness.13 The ligands, or bases, in the context of HSAB theory are Glu residues, water, hydroxide, and His residues. Glu, water, and hydroxide all bind to Fe through oxygen, a hard base. Fe(IV), Fe(III), and Fe(II) are the relevant metal oxidation states in MMO’s catalytic cycle. HSAB suggests Fe(IV) and Fe(III) exhibit hard acid character compatible for coordination with the oxygens that exhibit hard base character. Fe(II) has a lower charge density than Fe(III) and Fe(IV) resulting in borderline acid character. In the active site Fe(II) is most compatible with the nitrogen of His. Although nitrogen is typically a hard base, histidine's resonance increases the base’s polarizability to soften the base character of this residue; His is ultimately considered a borderline base. Since hard acids and hard bases are more likely to interact with atoms that are similar along the hard-soft scale, the hard Fe(IV), hard Fe(III), and borderline Fe(II) ions are suitable for the hard (Glu, H2O, and OH) and borderline (His) base. Additionally, the mixed coordination, consisting of hard and borderline bases, is ideal for the MMOH binding site in which Fe must cycle between hard and borderline states.
Ligand Field Theory (LFT)
Field splitting refers to creation of an energy gap (\(\Delta\)) between orbitals resulting from metal-ligand interactions. Different metal-ligand coordination geometries result in different orbital splitting. Ligand field theory (LFT) takes into consideration metal charge, coordination geometry, and ligand identity to understand electron spin and orbital splitting. The Fe(III) centers in MMOHox have a high spin d-orbital electron configuration.14 The high spin electrons follow the generalized trend that 1st row transition metals are typically high spin. High spin is further rationalized through consideration of Fe(III) ligands in the MMO active site.15 Coordinated to Fe(III), the oxygens of Glu, water, and hydroxide are \(\sigma\) donating and \(\pi\) donating ligands, which are weak field ligands in the spectrochemical series, shown below in Figure 6. \(\sigma\) and \(\pi\) donating ligands tend to decrease the magnitude of the octahedral d-orbital splitting (\(\Delta_{o}\)). Histidine is a \(\pi\) acceptor, but the \(\pi\) accepting is so weak such that this ligand is not is not considered a strong-field ligand.16
Overall, the ligand set favors a small \(\Delta_{o}\). Based on the position on the periodic table, the charge on Fe(II), and its generally weak-field ligand set, one would expect the Fe(II) of MMOH to be high spin. This analysis of the high spin Fe(II) complex is supported in literature.15 Considering octahedral d-orbital splitting, small \(\Delta_{o}\) values correspond with high spin metal complexes because electrons occupy higher energy orbital levels before pairing up in the lower energy orbitals. In other words, the energy to place electrons in higher energy orbitals levels is less than the energy cost of pairing, called pairing energy, for electrons in the lower energy d-orbitals. Low spin electron configurations result from large \(\Delta_{o}\) values that make the cost of pairing energy (PE) less than the cost of placing electrons in the higher energy d-orbitals. Thus, electrons prefer to pair when \(\Delta_{o}\) is large, shown in Figure 7.
Overall the iron oxidation states observed in the catalytic cycle include +2, +3, and +4, with 3d-electron counts of 6, 5, and 4, respectively. These oxidation states result from MMOHox reduction to MMOHred, and oxidation reactions to form P and Q diiron clusters. The Fe(II), Fe(III), and Fe(IV) are high spin for all intermediates.6,14 These irons have low crystal field splitting energies (\(\Delta\)), meaning the gap between split d-orbital energies is small enough smaller such that electrons can move into the higher energy d-orbitals before pairing in the lower energy d-orbitals. This small \(\Delta\) results in a weak field and high spin complex, shown above in Figure 7. When transition metal cations are octahedrally coordinated with 6 ligands, the d-orbitals split in energy with three lower energy (eg) and 2 higher energy (t2g) orbitals. Based upon ligand field stabilization energy (LFSE) calculations for octahedral geometry the LFSE of low spin Fe(III) is -2\(\Delta_{o}\) and the LFSE of high spin Fe(III) is 0\(\Delta_{o}\). Stabilization energy (SE) calculations include LFSE to characterize a complex’s thermodynamic stability. However, thermodynamic stability also depends upon pairing energy (PE) of electrons. SE is the sum of LFSE and PE values. For high spin 3d metals, PE is greater than LFSE such that it is more favorable to enter higher energy orbitals than to pair up in lower orbitals. For octahedral complexes, higher \(\Delta_{o}\) magnitude results in more negative LFSE, and thus more negative SE values that correspond to increased thermodynamic stability. Thus, other factors such as sterics between ligands as well as protein folding constraints must be considered to understand the octahedral geometry.5 The folded protein may dictate the coordination around the Fe ions though sterics, where six ligands are optimally spread out in octahedral geometry. If metal ion size also influences the coordination bond length, then the octahedral coordination may be selective for ions with a similar ionic radius as Fe(III). Moreover, the amino acid residues stabilize the complex to increase thermodynamic stability.6,7
Kinetics
In metal-ligand complexes, kinetics are used to understand ligand exchange. A labile metal complex has kinetically fast ligand exchange. Inert metal complexes have kinetically slow ligand exchanges and intermediate metal complexes have kinetically intermediate substitutions. Lability depends upon factors like d-electron count, metal charge, metal ionic radius, and metal-ligand antibonding occupancy. Fe(II) has a high spin d6 electrons that are considered kinetically labile because the electrons occupy the antibonding orbitals of the octahedral complex, which are eg orbitals shown in Figure 7. The kinetic lability of Fe(II) is advantageous for fast ligand exchange between intermediate O and intermediate P* of the catalytic cycle, depicted in the MMO catalytic cycle section in Figure 5. High spin Fe(III) has 2 electrons in the eg orbitals and Fe(IV) has 1 electron in the eg orbital. With the existence of one or more electron(s) in the eg orbital for high spin Fe(II), Fe(III), and Fe(IV), one would expect all three oxidation states to be kinetically labile. Compared to Fe(III) and Fe(IV), the Fe(II) has a low metal charge and a larger ionic radius. As metal ion charge increases, ionic radii decreases and the metal complex becomes less labile, or more inert. This phenomenon is rationalized by Coulomb’s Law, which explains that force of attraction between ions increases when ion charge increases and ionic radius decreases. Thus, among the relevant Fe ions, Fe(II) is the most kinetically labile followed by Fe(III) being less labile and Fe(IV) being the least labile. In the context of the catalytic cycle, the labile Fe(II) is important for ligand substitution in the conversion of O to P*. Lability is also important for the ligand exchange in Fe(III)-containing MMOHox, which undergoes a solvent ligand to Glu ligand exchange to form MMOHred. Decay of intermediate T also appears to require liability for ligand association for the Fe(III)-containing active site. Lastly, lability is important for ligand dissociation between intermediate R, with Fe(IV)-Fe(III) to intermediate T. Overall, the Fe(II), Fe(III), and Fe(IV) complexes must all be capable of ligand gaining, losing, or exchanging ligands.
Redox and Electron Transfer
Reduction of MMOHox
MMOR oxidizes NADH to obtain electrons to transfer to MMOH’s oxidized resting state. Subsequently, reduction occurs through electron transfer from MMOR to MMOHox. Figure 8 below depicts this reaction.
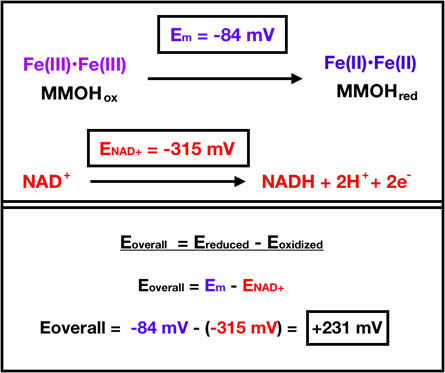
In the overall reaction, MMOHox is reduced and NADH is oxidized. For MMOHox, the reduction midpoint potential (Em) is reported to be -84 mV per electron, which comes from the average of -52 mV for the first electron and -115 mV for the second electron.11 For ease of calculation, the overall potential (Eoverall) used here includes the reduction midpoint. The reduction potential for NAD+ (ENAD+) is -315 mV.11 When the Eoverall is positive, a reaction is considered spontaneous. The Eoverall is calculated as the reduction potential of the reduced species minus the reduction potential of the oxidized species. In the case of the MMOHox reduction reaction, an Eoverall calculation yields 231 mV, shown above in Figure 8. Since Eoverall is positive, the reaction for MMOHox reduction is considered spontaneous.
Redox in Oxygen Activation and Methane Oxidation
Oxygen activation occurs in the conversion of intermediate P* to intermediate P. This conversion occurs via a metal-to-ligand transfer of electrons in which the two Fe(III) are oxidized and \(\ce{O_{2}}\) is reduced, resulting in two Fe(II) and a bridging peroxide. To determine Eoverall, iron one can regard iron as “free” iron and the bridging peroxide as peroxide (\(\ce{H_{2}O_{2}}\)). Oxygen undergoes a two-electron reduction because one-electron reductions of oxygen are unfavorable.17 The reduction potential of \(\ce{O_{2}}\) to \(\ce{H_{2}O_{2}}\) is +281 mV.18 For Fe(II) reduction to Fe(III), the reduction potential is +771 mV.18 Considering these reduction potentials, the overall potential for the conversion of P* to P is +490 mV from equation 1 and equation 2 below. Since Eoverall is positive, this reaction of P* to P is considered spontaneous.
\[\ce{E_{overall}} = \ce{E_{Fe(III)}} - \ce{E_{H_{2}O_{2}}} \label{1}\]
\[\ce{E_{overall}} = +771 mV - (+281 mV) = +490 mV \label{2}\]
Methane Oxidation
Methane oxidation occurs during the decay of intermediate Q. The first step of Q decay involves \(\ce{CH_{4}}\) reacting with Fe(IV) in a one-electron redox reaction to produce methane radical, \(\ce{H^{+}}\), and Fe(III). In this case, \(\ce{CH_{4}}\) is oxidized to form •\(\ce{CH_{3}}\) and one Fe(IV) in the active site is reduced to Fe(III). Reduction potentials have not been reported for these half-reactions; however one would expect a positive overall potential for the reaction to be favorable.
Summary
In conclusion, soluble methane monooxygenase (MMO) is an oxygen activating enzyme that catalyzes selective oxidation of methane (\(\ce{CH_{4}}\)) to methanol (\(\ce{CH_{3}OH}\)). This reaction is important for industries to inexpensively convert a potent greenhouse gas, \(\ce{CH_{4}}\), to a more easily used form of energy, \(\ce{CH_{3}OH}\). Found in methane consuming bacteria, this enzyme’s catalytic activity has been studied for the sake of developing a catalyst that can efficiently oxidize methane in the lab and in industry. Application of bioinorganic concepts can be used to better understand the diiron site of MMO. Hard-soft acid-base theory indicates Fe(III) and Fe(IV) have hard acid character that is compatible with the oxygens from glutamic acid (Glu), water, and hydroxide that coordinate to the metal centers. The borderline nitrogen in histidine (His) at the active site is compatible with the borderline Fe(II) ion. Ligand field theory explains that the Fe(II), Fe(III), and Fe(IV) are high spin with low crystal field splitting energies. The Glu, water, and hydroxide are \(\sigma\) donating and \(\pi\) donating ligands and the His is a weak \(\pi\) accepting ligand. Focusing on the resting state of the enzyme, MMOHox, the iron ions are pseudo-octahedrally coordinated, and follow octahedral d-orbital splitting. Sterics within the active site contribute to the stability of this pseudo-octahedral complex. Lastly, kinetics explains that the Fe(II)-containing intermediates are the most kinetically labile, followed by Fe(III), and Fe(IV). Considering the change in oxidation state of the MMOH’s metal center, redox and electron transfer are integral steps within MMOH’s catalysis cycle.
Sources
- Wang, W.; Liang, A. D.; Lippard, S. J. Coupling Oxygen Consumption with Hydrocarbon Oxidation in Bacterial Multicomponent Monooxygenases. Acc. Chem. Res. 2015, 48 (9), 2632–2639. https://doi.org/10.1021/acs.accounts.5b00312.
- Han, B.; Yang, Y.; Xu, Y.; Etim, U. J.; Qiao, K.; Xu, B.; Yan, Z. A Review of the Direct Oxidation of Methane to Methanol. Chinese Journal of Catalysis 2016, 37 (8), 1206–1215. https://doi.org/10.1016/S1872-2067(15)61097-X.
- Alvarez-Galvan, M. C.; Mota, N.; Ojeda, M.; Rojas, S.; Navarro, R. M.; Fierro, J. L. G. Direct Methane Conversion Routes to Chemicals and Fuels. Catalysis Today 2011, 171 (1), 15–23. https://doi.org/10.1016/j.cattod.2011.02.028.
- Pham, M. D.; Lin, Y.-P.; Van Vuong, Q.; Nagababu, P.; Chang, B. T.-A.; Ng, K. Y.; Chen, C.-H.; Han, C.-C.; Chen, C.-H.; Li, M. S.; Yu, S. S.-F.; Chan, S. I. Inactivation of the Particulate Methane Monooxygenase (PMMO) in Methylococcus Capsulatus (Bath) by Acetylene. Biochimica et Biophysica Acta (BBA) - Proteins and Proteomics 2015, 1854 (12), 1842–1852. https://doi.org/10.1016/j.bbapap.2015.08.004.
- Patt, T. E.; Hanson, R. S. Intracytoplasmic Membrane, Phospholipid, and Sterol Content of Methylobacterium Organophilum Cells Grown under Different Conditions. J Bacteriol 1978, 134 (2), 636–644.
- Banerjee, R.; Jones, J. C.; Lipscomb, J. D. Soluble Methane Monooxygenase. 2019, 88 (1), 409–431. https://doi.org/10.1146/annurev-biochem-013118-111529.
- Sazinsky, M. H.; Merkx, M.; Cadieux, E.; Tang, S.; Lippard, S. J. Preparation and X-Ray Structures of Metal-Free, Dicobalt and Dimanganese Forms of Soluble Methane Monooxygenase Hydroxylase from Methylococcus Capsulatus (Bath). Biochemistry 2004, 43 (51), 16263–16276. https://doi.org/10.1021/bi048140z.
- Huang, X.; Groves, J. T. Oxygen Activation and Radical Transformations in Heme Proteins and Metalloporphyrins. Chem. Rev. 2018, 118 (5), 2491–2553. https://doi.org/10.1021/acs.chemrev.7b00373.
- Bertini, I.; Gray; Stiefel, J.; Valentine. Biological Inorganic Chemistry: Structure & Reactivity; University Science Books, 2007, 388 - 410.
- Banerjee, R.; Meier, K. K.; Münck, E.; Lipscomb, J. D. Intermediate P* from Soluble Methane Monooxygenase Contains a Diferrous Cluster. Biochemistry 2013, 52 (25), 4331–4342. https://doi.org/10.1021/bi400182
- Paulsen, K. E.; Liu, Y.; Fox, B. G.; Lipscomb, J. D.; Munck, E.; Stankovich, M. T. Oxidation-Reduction Potentials of the Methane Monooxygenase Hydroxylase Component from Methylosinus Trichosporium OB3b. Biochemistry 1994, 33 (3), 713–722. https://doi.org/10.1021/bi00169a013.
- Cárdenas, C.; Ayers, P. W. How Reliable Is the Hard–Soft Acid–Base Principle? An Assessment from Numerical Simulations of Electron Transfer Energies. Phys. Chem. Chem. Phys. 2013, 15 (33), 13959–13968. https://doi.org/10.1039/C3CP51134K.
- Pulver, S. C.; Froland, W. A.; Lipscomb, J. D.; Solomon, E. I. Ligand Field Circular Dichroism and Magnetic Circular Dichroism Studies of Component B and Substrate Binding to the Hydroxylase Component of Methane Monooxygenase. J. Am. Chem. Soc. 1997, 119 (2), 387–395. https://doi.org/10.1021/ja962854i.
- Turitsyna, E. A.; Trukhan, V. M.; Shteinman, A. A. Synthesis and Structure of Binuclear Iron(Ii) Complex with the Cage-like Ligand as a Model of Methane Monooxygenase. Russ Chem Bull 2011, 60 (10), 2088–2093. https://doi.org/10.1007/s11172-011-0319-0.
- Sundberg, R. B. Martin, Chemical Reviews 1974, 74, 471-517.
- Voet, D.; Voet, J. G.; Pratt, C. W. Fundamentals of Biochemistry: Life at the Molecular Level; John Wiley & Sons, 2016.
- Metz, M.; Solomon, E. I. Dioxygen Binding to Deoxyhemocyanin: Electronic Structure and Mechanism of the Spin-Forbidden Two-Electron Reduction of O2. J. Am. Chem. Soc. 2001, 123 (21), 4938–4950. https://doi.org/10.1021/ja004166b.
- Lippard, S. J.; Berg, J. M. Principles of Bioinorganic Chemistry; University Science Books, 1994.
Contributed by:
Chiara Smorada, a chemistry major at Saint Mary's College, class of 2020.

