Skip to main content
Chemistry LibreTexts

3.7: Conformational analysis

  1. Last updated
  2. Save as PDF
  • Page ID
    225777

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Conformational analysis is the study of the energetics between different rotamers and is useful for understanding the stability of different isomers by taking into account the spatial orientation and through-space interactions of substituents. Conformational analysis can be used to predict and explain product(s) selectivity, mechanisms, and rates of reactions.  We will not go into such detail, but we will be taking the principles learnt in cases such as butane and methylcyclohexane, and applying them to more complex alkanes.

    Open-chain (acyclic) conformations

    Ethane and propane

    We have already seen how the eclipsed form of these alkanes is higher in energy than the staggered form, by around 12-14 kJ/mol (3-3.4 kcal/mol), which can be considered as the sum of three eclipsed interactions.

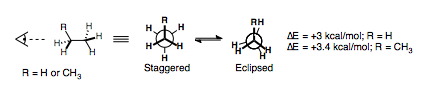
    Ethane-Propane.png
    Eclipsed interaction Energy (kcal/mol) Energy (kJ/mol)
    H||H 1.0 4.0
    H||CH3 1.4 6.0

    Butane

    Once we examine butane, we have a new eclipsed interaction, CH3||CH3,for which the energy value can be estimated from from the overall energy difference (found experimentally to be 5.1 kcal/mol).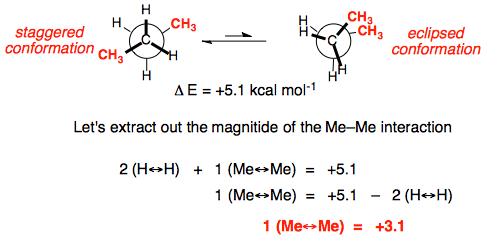
    butane-eclipsed2.pngThus we can see that the interaction between eclipsing methyl groups is worth 3.1 kcal/mol or 13 kJ/mol – much more than the H||CH3 interaction we saw first in propane.

    Higher alkanes

    Butane shows us that the eclipsing of two methyl groups + two H groups destabilizes more than eclipsing of two H||CH3 pairs.  This indicates a general principle, that Big-Big eclipsing interactions are the most destabilizing. This can be remembered as “Big-Big is Bad“! Experimental studies show that this generally applies both when judging the least stable conformations (where big-big eclipsing is most destabilizing) and when judging the most stable conformations (where gauche interactions are destabilizing relative to anti conformations).

    For example: Consider 2-methylbutane – what is/are the most stable conformation(s)?  What is/are the least?

    HINT: It can help to make a molecular model of the compound, and draw a Newman projection.  Then rotate one end of the bond through 60o intervals until you have get back to where you started.  In the figure below, the front end of the bond is rotating clockwise, going from 1 to 2, etc.

    2methylbutaneConformations1.gif

    For this class, we will always find that the most stable conformation is staggered (i.e., 1, 3 or 5), and the least stable is eclipsed (i.e., 2, 4 or 6).  Comparing 1, 3 and 5, we see that 1 has two “bad” gauche interactions, whereas 3 and 5 have only one gauche interaction; thus 3 and 5 are both equally stable, and they are the most stable conformations for 2-methylbutane.  Comparing 2, 4 and 6, we see that 2 and 6 both involve one “Big-Big” (methyl-methyl) interaction, but 4 does not.  Thus 4 is the least unstable of the eclipsed forms, and 2 and 6 are equally unstable so they are the least stable conformations.

    In cases where the big groups are ethyl, propyl, etc., rather than just methyl, these groups will count as bigger than methyl when judging their destabilizing effects.  Branched alkyls such as isopropyl (-CH(CH3)2) are more destabilizing, with tertiary groups such as tert-butyl (-C(CH3)3) the most destabilizing of all, reflecting their steric bulk.

    Substituted cyclohexanes​

    A Values

    Substituents on a cyclohexane prefer to be in the equatorial position.  When a substituent is in the axial position, there are two gauche butane interactions more than when a substituent is in the equatorial position. We quantify the energy difference between the axial and equatorial conformations as the A-value, which is equivalent to the negative of the ∆G°, for the equilibrium shown below. Therefore the A-value, or -∆G°, is the preference for the substituent to sit in the equatorial position.

    A-Values.png

    Recall that the equilibrium constant is related to the change in Gibbs Energies for the reaction:

    ∆G° = –RT 1nKeq

    The balance between reactants and products in a reaction will be determined by the free energy difference between the two sides of the reaction. The greater the free energy difference, the more the reaction will favor one side or the other.

    Table: Below is a table of A-values for some common substituents.

    Substituent ∆G° (kcal/mol) A-value
    -F -0.28-0.24 0.24-0.28
    -Cl -0.53 0.53
    -Br -0.48 0.48
    -I -0.47 0.47
    -CH3 (-Me) -1.8 1.8
    -CH2CH3 (-Et) -1.8 1.8
    -CH(CH3)2 (-i-Pr) -2.1 2.1
    -C(CH3)3 (-t-Bu) <-4.5 >4.5
    -CH=CH2 -1.7 1.7
    -C=CH -0.5 0.5
    -CN -0.25-0.15 0.15-0.25
    -C6H5 (-Ph) -2.9 2.9

    This table allows us to estimate the actual energy differences between conformations with axial vs. equatorial substituents.  However, in general, to stablize we simply place bigger groups equatorial.  To find the most stable conformation, we choose the form with the least number of large axial groups; the least stable will have the most number of axial groups.

    When “big” groups come in close proximity (e.g., two methyls on neighboring carbons on a cyclohexane ring), the “Big-Big is Bad” principle applies, as it did with open-chain alkanes.

    Polysubstituted cyclohexanes

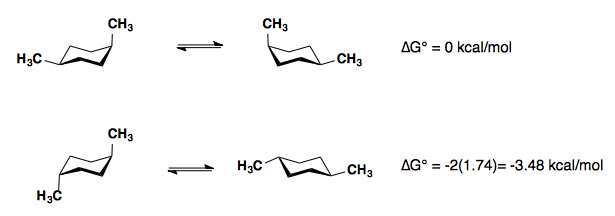
    1,4-disubstitution

    The A-values of the substituents are roughly additive in either the cis– or trans-diastereomers.

    1,4-disubstitutions.png

    1,3-disubstitution

    ​A-values are only additive in the trans-diastereomer:

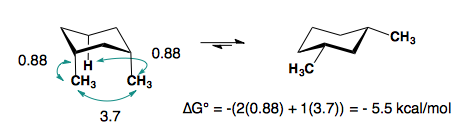
    12C3_cis_cyclohexane.png

    When there are cis-substituents on the chair, there is a new interaction in the di-axial conformation:

    In the above example, each methyl group has one 1,3-diaxial interaction with a hydrogen. The methyl groups also interact with each other.  This new diaxial interaction is extremely unfavorable based on their steric interaction (double-gauche pentane conformation. a “big-big” interaction).

    Practice Problems

    Practice problems

    static_qr_code_without_logo1-150x150.png
    CC licensed content, Original
    CC licensed content, Shared previously

    3.7: Conformational analysis is shared under a not declared license and was authored, remixed, and/or curated by LibreTexts.

    1. Back to top
    • Was this article helpful?

    Recommended articles

    1. Article type
      Section or Page
    2. Tags
      This page has no tags.