Cyclic Conformations
- Page ID
- 20933
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Types of Strain
There are three types of strain associated with cyclic conformations:
- Prelog Strain: Van der Waals interactions
- Baeyer Strain: Bond angle distortion away from the ideal
- Pitzer Strain: Torsional rotation about a sigma bond
Baeyer Strain
| Size of Ring | Heat of Combustion (kcal/mol) | Total Strain (kcal/mol) | Strain per "CH2" (kcal/mol) | "Angle Strain" deviation from 109°28' |
| 3 | 499.8 | 27.5 | 9.17 | 24°44' |
| 4 | 656.1 | 26.3 | 6.58 | 9°44' |
| 5 | 793.5 | 6.2 | 1.24 | 0°44' |
| 6 | 944.8 | 0.1 | 0.02 | -5°16' |
| 7 | 1108.3 | 6.2 | 0.89 | -- |
| 8 | 1269.2 | 9.7 | 1.21 | -- |
| 9 | 1429.6 | 12.6 | 1.40 | -- |
| 10 | 1586.8 | 12.4 | 1.24 | -- |
| 11 | 1743.1 | 11.3 | 1.02 | -- |
| 12 | 1893.4 | 4.1 | 0.34 | -- |
| 13 | 2051.9 | 5.2 | 0.40 | -- |
| 14 | 2206.1 | 1.9 | 0.14 | -- |
| 15 | 2363.5 | 1.9 | 0.13 | -- |
Substituted Cyclohexanes
A Values
Substituents on a cyclohexane prefer to be in the equatorial position. When a substituent is in the axial position, there are two gauche butane interactions more than when a substituent is in the equatorial position. We quantify the energy difference between the axial and equatorial conformations as the A-value, which is equivalent to the negative of the ∆G°, for the equilibrium shown below. Therefore the A-value, or -∆G°, is the preference for the substituent to sit in the equatorial position.

Recall that the equilibrium constant is related to the change in Gibbs Energies for the reaction:
\[\Delta{G^o} = -RT\ln {K_{eq}}\]
The balance between reactants and products in a reaction will be determined by the free energy difference between the two sides of the reaction. The greater the free energy difference, the more the reaction will favor one side or the other.
Table: Below is a table of A-values for some common substituents.
| Substituent | ∆G° (kcal/mol) | A-value |
| -F | -0.28-0.24 | 0.24-0.28 |
| -Cl | -0.53 | 0.53 |
| -Br | -0.48 | 0.48 |
| -I | -0.47 | 0.47 |
| -CH3 (-Me) | -1.8 | 1.8 |
| -CH2CH3 (-Et) | -1.8 | 1.8 |
| -CH(CH3)2 (-i-Pr) | -2.1 | 2.1 |
| -C(CH3)3 (-t-Bu) | <-4.5 | >4.5 |
| -CHCH2 | -1.7 | 1.7 |
| -CCH | -0.5 | 0.5 |
| -CN | -0.25-0.15 | 0.15-0.25 |
| -C6H5 (-Ph) | -2.9 | 2.9 |
Polysubstituted Cyclohexanes
1,4-disubstitution
The A-values of the substituents are roughly additive in either the cis- or trans-diastereomers.
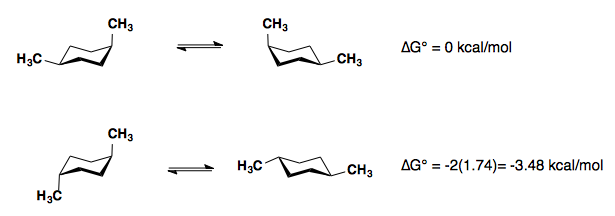
1,3-disubstitution
A-values are only additive in the trans-diastereomer:
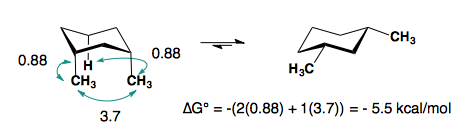
When there are cis-substituents on the chair, there is a new interaction in the di-axial conformation:
In the above example, each methyl group has one 1,3-diaxial interaction with a hydrogen. The methyl groups also interact with each other. This new diaxial interaction is extremely unfavorable based on their steric interaction (see: double-gauche pentane conformation).
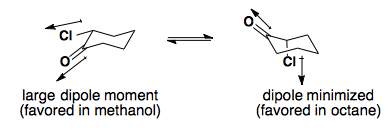
Solvent Effects
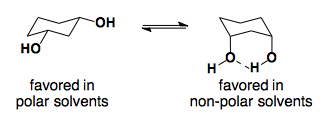
Substituted Cyclohexanones
Saturated Heterocyclic 6-member Rings
Anomeric Effect
In 2-substituted pyranose rings, some substituents prefer to sit in the axial conformation.
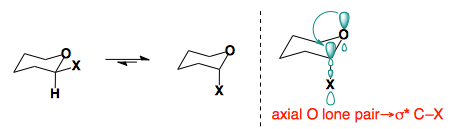
This preference arises from orbital interactions between the oxygen lone pair and the low-lying σ* of the C–X bond. This effect which provides the stabilization of the axial conformer, which overrides the inherent steric bias of the substituents, is reffered to as the anomeric effect.
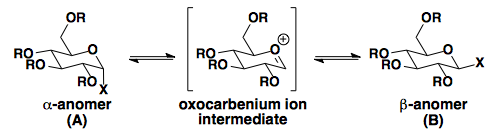
| X | R | % A | % B | Solvent (25 °C) |
| OH | H | 36 | 64 | H2O |
| OCH3 | H | 67 | 44 | CH3OH |
| OAc | Ac | 86 | 14 | AcOH |
| Cl | Ac | 94 | 6 | CH3CN |
As seen in the table, X groups with better σ*-accepting capabilities are most affected by the anomeric effect.
Talaromycin B
In the synthesis of Talaromycin B, Schreiber noticed the lowest energy conformation of the molecule sits with all of the substituents in equatorial positions. In this conformation, the spircyclic center also prefers a conformation stabilized by two anomeric effects. Understanding the thermodynamic preference for this conformation, Schreiber could disconnect at the spirocenter and concentrate on the synthesis of a linear precursor.
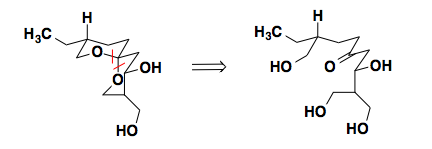
For the full synthetic sequence see: Tetrahedron Lett., 1983, 24, 4781-4784.
Unsaturated Ring Systems
Cylcohexenes
Cyclohexenes adopt half-chair conformations which are pictured below. Substituents prefer to sit in the pseudo-equatorial or equatorial positions of the ring.
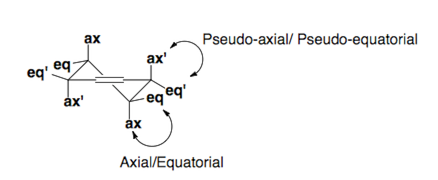
Fürst-Plattner Rule
The Fürst-Plattner rule accounts for the observed stereochemical outcome from the nucleophilic addition to cyclohexenes and cyclohexene-like systems (ex: bicyclic epoxides, oxonium ions, etc.). Nucleophiles will react with these systems to yield the trans-diaxial addition product. This selectivity arises from torsional strain which builds in the transition state of the reaction.
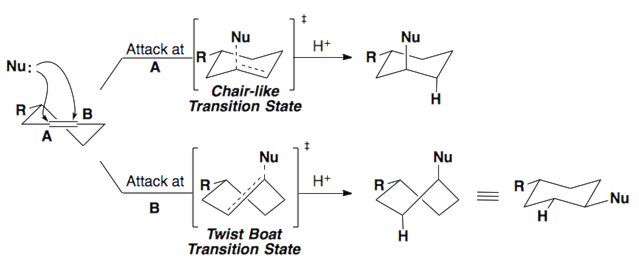
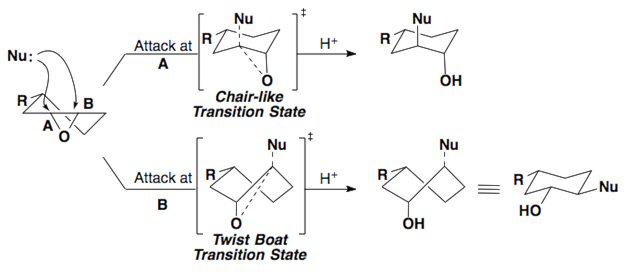
These same rules can be applied to epoxides.
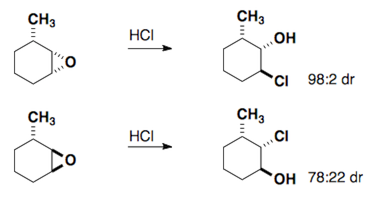
Here are a few examples of the Fürst-Plattner rule. Attempt to draw out the correct half-chair that leads to the product for each of these cases.
Bicyclic Ring Systems
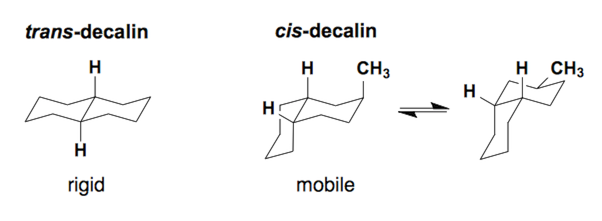
Decalin ring system (6/6)
Decalins can come in two diastereomers, the trans- or cis- diastereomer. The trans-diastereomer is a rigid structure which cannot undergo a ring flip. The cis-diastereomer is mobile and can ring flip to allow substituents to sit in the equatorial position.