3.5: Conformations of chain alkanes
- Page ID
- 225775
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Conformations
Before we begin our exploration of stereochemistry and chirality, we first need to consider the subject of conformational isomerism, which has to do with rotation about single bonds.
We learned in section 2.1 that single bonds in organic molecules are free to rotate, due to the ‘end-to-end’ (sigma) nature of their orbital overlap. Consider the carbon-oxygen bond in ethanol, for example: with a 180o rotation about this bond, the shape of the molecule would look quite different:
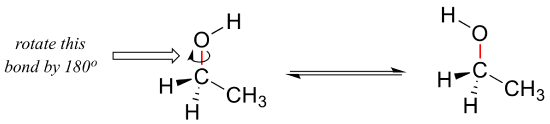
Or ethane: rotation about the carbon-carbon sigma bond results in many different possible three-dimensional arrangements of the atoms.

These different arrangements, resulting from sigma bond rotation, are referred to in organic chemistry as conformations. Any one specific conformation is called a conformational isomer, or conformer.
Newman projections
A representation of a molecule in which the atoms and bonds are viewed along the axis about which rotation occurs is called a Newman projection.
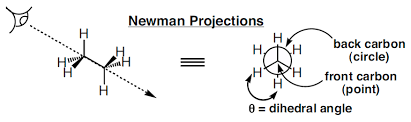
In a Newman projection, the molecule is viewed along an axis containing two atoms bonded to each other and the bond between them, about which the molecule can rotate. In a Newman projection, the “substituents” of each atom composing the bond, be they hydrogens or functional groups, can then be viewed both in front of and behind the carbon-carbon bond. Specifically, one can observe the angle between a substituent on the front atom and a substituent on the back atom in the Newman projection, which is called the dihedral angle or torsion angle.
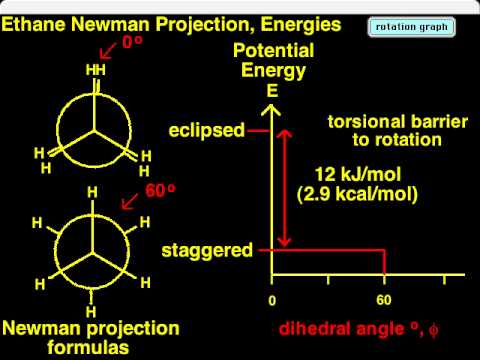
In ethane specifically, we can imagine two possible “extreme” conformations. In one case, the dihedral angle is 0° and the hydrogens on the first carbon line up with or eclipse the hydrogens on the second carbon. When the dihedral angle is 0° and the hydrogens line up perfectly, ethane has adopted the eclipsed conformation (see figure). The other extreme occurs when the hydrogens on the first carbon are as far away as possible from those on the second carbon; this occurs at a dihedral angle of 60° and is called the staggered conformation.
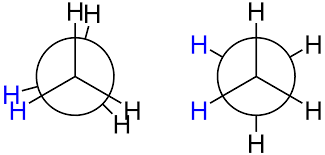
The staggered conformation of ethane is a more stable, lower energy conformation than the eclipsed conformation because the eclipsed conformation involves unfavorable interactions between hydrogen atoms. Specifically, the negatively charged electrons in the bonds repel each other most when the bonds line up. Thus, ethane spends most of its time in the more stable staggered conformation.
The six carbon-hydrogen bonds are shown as solid lines protruding from the two carbons. Note that we do not draw bonds as solid or dashed wedges in a Newman projection.
Ethane
The lowest energy conformation of ethane, shown in the figure above, is called the ‘staggered’ conformation: all of the dihedral angles are 60o, and the distance between the front and back C-H bonds is maximized.
If we now rotate the front CH3 group 60° clockwise, the molecule is in the highest energy ‘eclipsed’ conformation, where the dihedral angles are all 0o (we stagger the bonds slightly in our Newman projection drawing so that we can see them all).

This brings the electrons in the front and back C-H bonds closer together, and there is repulsion between them. The energy of the eclipsed conformation is approximately 12 kJ/mol higher (less stable) than that of the staggered conformation. Rotation then is not strictly “free” because there is a 12 kJ/mol energy barrier to overcome on eclipsing the hydrogens. Even so, the barrier is low enough that rotation is very rapid at room temperature, occurring on the order of $$10^{10}$$ times per second.
It is very useful to create models of these conformations using your molecular model kit. The two main conformations of ethane are shown here as ball-and-stick drawings:
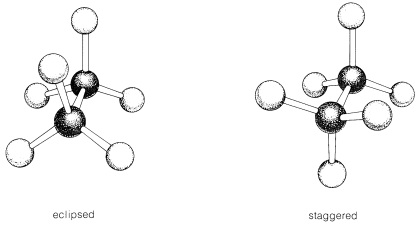
Another 60° rotation returns the molecule to a second staggered conformation. This process can be continued all around the 360° circle, with three possible eclipsed conformations and three staggered conformations, in addition to an infinite number of conformations in between these two extremes, as shown in this short video by DokeDJ:

Propane
If one looks at one of the C-C bonds in propane (three carbons), it has the same type of graph, but the energy difference between staggered and eclipsed is slightly higher 14 kJ/mol. See Wallace’s analysis.
Butane
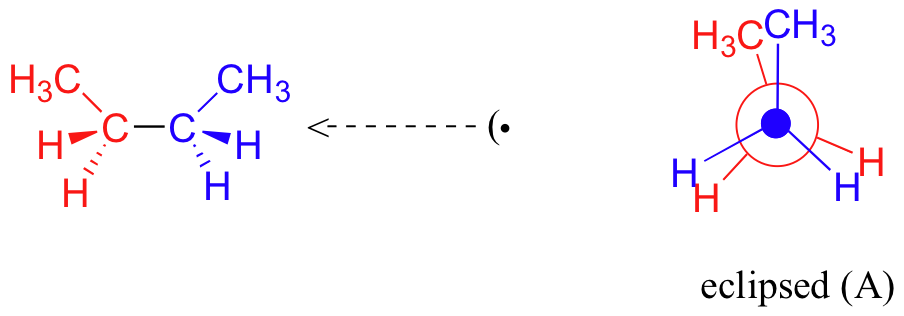
Now let’s consider butane, with its four-carbon chain. There are now three rotating carbon-carbon bonds to consider, but we will focus on the middle bond between C2 and C3. Below are two representations of butane in a conformation which puts the two CH3 groups (C1 and C4) in the eclipsed position, with the two C-C bonds at a 0o dihedral angle. With cases like this, space-filling models usually show less interference (steric hindrance) for staggered conformations than for eclipsed conformations, .
If we rotate the front, (blue) carbon by 60° clockwise, the butane molecule is now in a staggered conformation.
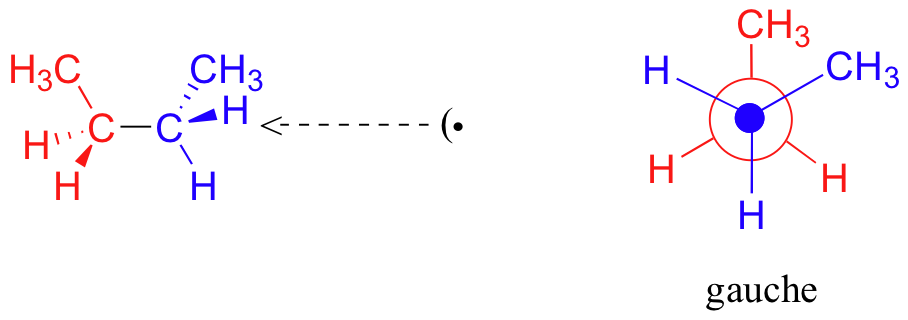
This is more specifically referred to as the gauche conformation of butane. Notice that although they are staggered, the two methyl groups are not as far apart as they could possibly be.
A further rotation of 60° gives us a second eclipsed conformation (B) in which both methyl groups are lined up with hydrogen atoms.
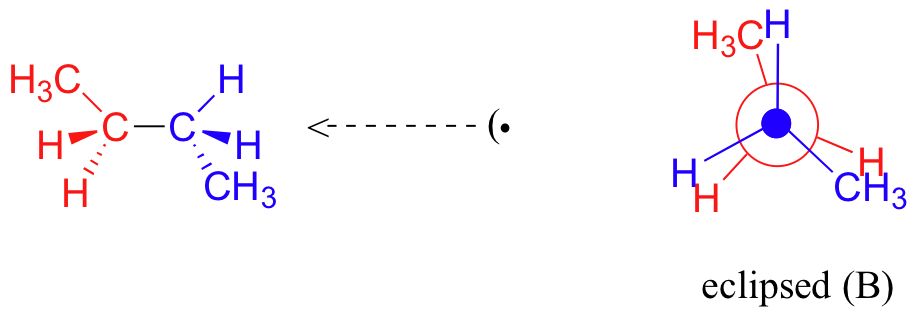
One more 60 rotation produces another staggered conformation called the anti conformation, where the two methyl groups are positioned opposite each other (a dihedral angle of 180o).
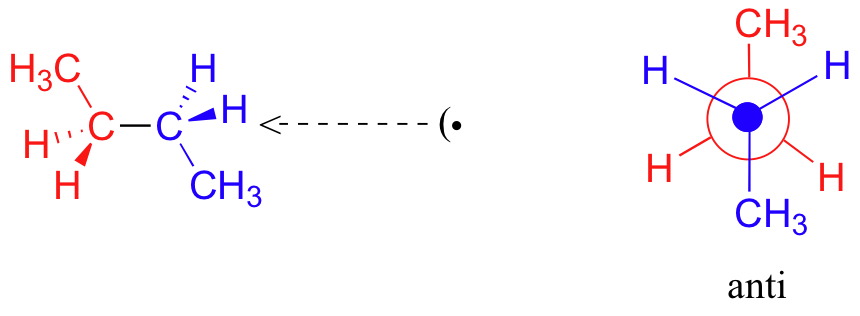
Thus we see that there are four possible “extreme” conformations of butane: 1) Fully eclipsed, when the methyl groups eclipse each other; 2) Gauche, when the methyl groups are staggered but next to each other; 3) Eclipsed, when the methyl groups eclipse hydrogen atoms; and 4) Anti, when the methyl groups are staggered and as far away from each other as possible (Figure 4).
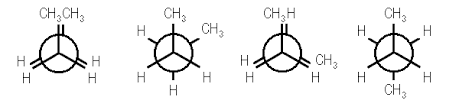
The fully eclipsed conformation is clearly the highest in energy and least favorable since the largest groups are interacting directly with each other. As the molecule rotates, it adopts the relatively stable gauche conformation. As it continues to rotate, it encounters less favorable eclipsed conformation in which a methyl group eclipses a hydrogen. As rotation continues, the molecule comes to the anti conformation, which is the most stable since the substituents are staggered and the methyl groups are as far away from each other as possible. An energy diagram is a graph which represents the energy of a molecule as a function of some changing parameter. An energy diagram can be made as a function of dihedral angle for butane (Figure 5).
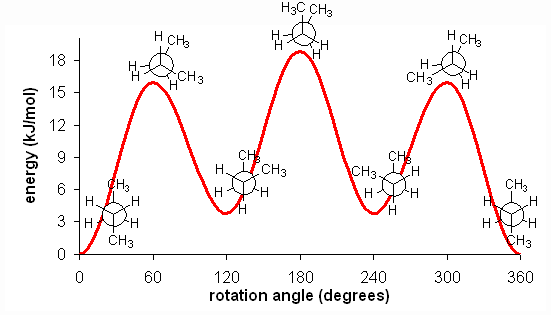
Clearly, the anti and gauche conformations are significantly more stable than the eclipsed and fully eclipsed conformations. Butane spends most of its time in the anti and gauche conformations. As with ethane, the staggered conformations of butane are energy ‘valleys’, and the eclipsed conformations are energy ‘peaks’. However, in the case of butane there are two different valleys, and two different peaks. The gauche conformation is a higher energy valley than the anti conformation due to steric strain, which is the repulsive interaction caused by the two bulky methyl groups being forced too close together. Clearly, steric strain is lower in the anti conformation.
There is one final, very important point. At room temperature, approximately 84 kJ/mol of thermal energy is available to molecules. Thus, if the barrier to a rotation is less than 84 kJ/mol, the molecule will rotate. In ethane and butane, the barriers to rotation are significantly less than 84 kJ/mol. Therefore, even though the eclipsed conformations are unfavorable, the molecules are able to adopt them. In reality, since these conformations are not as stable, the molecules will quickly pass through them at room temperature and return a staggered conformation. Molecules are constantly converting between different staggered conformations all the time, quickly passing through eclipsed conformations in between. Thus, in alkanes, no single “true” conformation exists all the time; the molecule instead constantly converts between conformations, spending more time in those that are more stable. This constant conversion lies in stark contract to alkenes, which adopt the cis- or trans- (E- or Z-) conformations and retain them at room temperature; they do not interconvert because the barrier to rotation is too high.
In the same way, steric strain causes the eclipsed A conformation – where the two methyl groups are as close together as they can possibly be – to be higher in energy than the two eclipsed B conformations. The six main conformations can be seen in this ball-and-stick diagram:
Higher alkanes
Because the anti conformation is lowest in energy (and also simply for ease of drawing), it is conventional to draw open-chain alkanes in a ‘zigzag’ form, which implies anti conformation at all carbon-carbon bonds. The figure below shows, as an example, a Newman projection looking down the C2-C3 bond of octane.
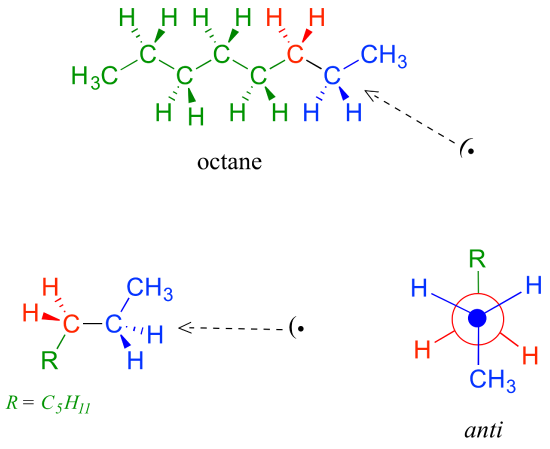
Problems involving conformations of higher alkanes will be covered in detail in section 3.7. Cyclic alkanes are dealt with in the next section.
Exercise 1
Draw Newman projections of the lowest and highest energy conformations of propane.
[reveal-answer q=”969353″]Show Solution[/reveal-answer]
[hidden-answer a=”969353″] [/hidden-answer]
[/hidden-answer]
Exercise 2
Draw a Newman projection, looking down the C2-C3 bond, of 1-butene in the conformation shown below (C2 should be your front carbon).
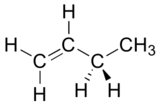
[reveal-answer q=”140251″]Show Solution[/reveal-answer]
[hidden-answer a=”140251″] [/hidden-answer]
[/hidden-answer]
Online lectures from Khan Academy
- 3.1: Conformations of open-chain organic molecules. Authored by: Tim Soderberg. Provided by: University of Minnesota Morris. Located at: https://chem.libretexts.org/Textbook_Maps/Organic_Chemistry/Book%3A_Organic_Chemistry_with_a_Biological_Emphasis_(Soderberg)/Chapter_03%3A_Conformations_and_Stereochemistry/03.1%3A_Conformations_of_straight-chain_organic_molecules%2C_Newman_projections. Project: Chemistry LibreTexts. License: CC BY-NC-SA: Attribution-NonCommercial-ShareAlike
- Alkanes Background. Authored by: Jim Clark, Jonathan Mooney . Provided by: McGill University. Located at: https://chem.libretexts.org/Core/Organic_Chemistry/Alkanes/Properties_of_Alkanes/Alkanes_Background. Project: Libretexts. License: CC BY-NC-SA: Attribution-NonCommercial-ShareAlike